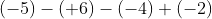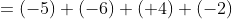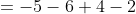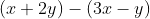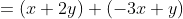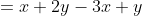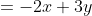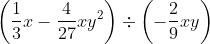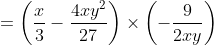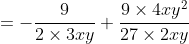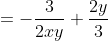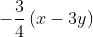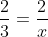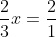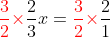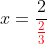こんにちは、塾長です。
数学の計算が苦手な人が、なぜ苦手なのか?
その理由と対処について、2年ほど前に私が書いた記事があります。まだアメブロで書いていた時代です。
今あらためて読んでみて、我ながら良く書けてるなぁ~と思ったので、このブログでも再掲しますね。
せっかくだから、少し読みやすく段組みして、言葉も補完してみました。
この時期は必見ですよ!
Contents
1学期前半の計算が数学の基礎!
学年を問わず、新学期の数学と言えば計算ですね。
ところで中学生以上の皆さん、あるいは、数学が超苦手な高校生の皆さん、
基本的に数学では、
「足し算と掛け算しか考えない!」
ということを、
ちゃんと守っていますか?
ちゃんと意識していますか?
ちゃんと使ってますか?
引き算と割り算は計算の邪魔!?
え、足し算と掛け算しかないって・・・じゃあ、引き算は? 割り算は?
と思われる方も多いでしょう。しかし数式の書き方で、
引き算は符号を逆にして足し算に、
割り算は逆数にして掛け算に、
直してから計算しましょう、と教わったことがあるはずですよ。更に、
足し算の記号(+)も、掛け算の記号(×)も書かない!
と教わりましたね。
足し算と掛け算しか考えないのであれば、書かなくても分かるでしょ!
ってことです。
それでは、なぜ、足し算と掛け算に統一するのか?
逆に、なぜ、引き算や割り算を避けるのか?
なぜだか分かりますか?
「交換法則」と答えたら不正解!?
それは以下の法則を使いまくりたいからです。
- 加法の交換法則: a+b = b+a
- 加法の結合法則: (a+b)+c =a+(b+c)
- 乗法の交換法則: a×b = b×a
- 乗法の結合法則: (a×b)×c =a×(b×c)
交換法則と結合法則は、引き算や割り算には通用しません。
学校のテストで
「交換法則」
と省略して書いたら減点されませんでしたか?
- 「加法の交換法則」
- 「乗法の交換法則」
と7文字すべてを書かないとダメでした。
これは、減法(引き算)や除法(割り算)にこの種の法則が成り立たないという事を強調したいからです。
(嫌みでもなければ、躾でもありません。数学の本質だからです。)
交換法則が成り立たない例
5-4=1
4-5=-1
16÷8=2
8÷16=0.5
小学校の時に、こんな間違いをしませんでしたか?
30÷3×2 = 30÷6 = 5
正しくは、
30÷3×2 = 10×2 = 20
でした。
交換法則や結合法則の通用しない割り算が式の中にあると、前から順に計算するしかないので不便です。
これが文字式になれば、もっと混乱するでしょう。
ですから、交換法則と結合法則がいつでも使える、掛け算と足し算だけにしておきたいのです。
足し算だけにすると負の数や式が使いやすくなる
さて、以下の書き方を見て、おさらいしましょう。
式1 (中1レベル)
引き算は足し算に直して
足し算の記号+と( )を省略して
最終的には足し算の記号+は書かない形になる!
つまり、
プラスの数とマイナスの数が並ぶだけの式になる!!
式2(中2レベル)
式の引き算は足し算に直して、
足し算の記号+と( )を省略して、
同類項をまとめて、
最終的には足し算の記号+や、掛け算の記号×を書かない形になる!
つまり、
プラスの項とマイナスの項が並ぶだけの式になる!!
掛け算だけにすれば分数の割り算だって楽になる
式3(中2レベル)
わり算は逆数のかけ算に直して、
分配法則でカッコを開いて、
( ↑ 約分しやすいように×記号を書くこともある )
最終的には足し算の記号+や、掛け算の記号×を書かない形になる!
つまり、
プラスの項とマイナスの項が並ぶだけの式になる!!
理解度チェック!
式の読み方1つで実力が判明!?
さあ、ここで理解度チェックです。次の数式を読んでみてください。
そんなの簡単じゃん、
『マイナスよんぶんのさん、かっこ、エックス ひく さんワイ、 かっこ。』
でしょ!
はい、ブブー!
え!?
・・・ ってなりますね。
『マイナスよんぶんのさん、かっこ、エックス マイナス さんワイ、かっこ。』
ですよ!
多項式を読むときに「マイナス」を「ひく」と読むのが間違いです。
ただし、この程度の読み方なら、間違っていても害はありません。どちらで読んでも正しく計算できる場合が多いからです。
とは言え、この読み間違いから、根本的に数式を理解していないことが分かります。
マイナス付け忘れた~
という符号ミスが多発する人は特に注意ですね。
計算ミスしやすい例題でチェック!
次の問題を解いてみましょう。
問: x = 2、y = -3 のとき、式 -xy の値を求めよ
- 悪い例: -xy = -2-3 = -5
- 良い例: -xy = -2×(-3) = 6
上の悪い例にある計算ミスは、式の意味が
-xy = (-1)×(x)×(y)
だという事を忘れてしまったか、あるいは、
-3 を「ひく3」
だと混同したことが原因です。
まとめ
- 数式は、数や項が並んでいるだけで、+や-の記号は、数や項の符号を表しています。
- つまり、プラス、マイナスと読むのであり、たす、ひくと読むのは勘違いです。
- 項が並んでいたら、それらは「たす」に決まっています。
- 項の中で数や文字が並んでいたら、それらは「かける」に決まっています。
- 逆に、文字式に数を代入する時は、必要に応じて足し算の+や掛け算の×を補わなければいけません。
さあ、これでめでたく、数式をできるだけ「足し算」と「掛け算」だけで考えるクセがつきました。
最後に以下の解き方を見て終わりましょう。
例題の追加!(中1の2学期以降)
次の方程式を解きましょう。
反比例の式について、y座標からx座標を求めるときに、このような方程式を解く場面がよく出て来ます。
両辺に x を掛けて、
ここまでは多くの生徒が同じように考えます。
さて、この次にどうするかで、中学生らしいか、そうでないのかが分かれます。
良くない例: 両辺に3をかけて、両辺を2で割る
これは割り算を使ってしまったので、よくありません。
中学生らしい解き方は、こうですね。
これなら一発で x=3 と答えが出ます。
方程式の解き方として、
「両辺を x の係数で割る」
と覚えている人は、覚え直しましょう。
先生!
って、どうやって計算するのですか?
なんて質問する羽目になって遠回りです。
ぜひ数学らしい式の計算を心掛け、ワンランク上を目指して欲しいと思います!
名古屋市天白区の植田で塾を探すなら個別指導のヒーローズ!!
★ 直接のお問い合わせ ★
――――――――――――――――――――――
個別指導ヒーローズ 植田一本松校
〒468-0009
名古屋市天白区元植田1-202 金光ビル2F
TEL:052-893-9759
教室の様子(360度カメラ) http://urx.blue/HCgL
――――――――――――――――――――――