塾長です。
新学期がはじまり1週間が経とうとしています。
みなさん、夏休みはどうでしたか、充実していました?
今年は夏休み中に稲武野外活動など学校行事が入ったところがありました。
そして今週から2学期がはじまったわけですが、
教室では中間テスト対策について、すでに案内とお申込みを始めております。
早い子はすでにスタートしております。
さて、今日のブログも塾長の趣味のお話です。
ここ半年間のプロジェクトで、やっと成果が出ました。
それをまとめたくて、勝手気ままに書きます。
天体望遠鏡が壊れた
私は小学生のころから天体観測が趣味でした。
今から20年以上前に、天体望遠鏡を動かす装置(写真の黄色の部分)を買いました。
サラリーマンになって間もなく、まだ給料が上がる前のこと。
これがけっこう高価でローンを組んで買ったのでした。

赤道儀とは天体望遠鏡を動かす台の部分(2008年9月)
しかし、10年くらい前にそれが壊れて動かなくなってしまいました。
高価なので、修理も買い替えも、なかなかできません。
ところで、この望遠鏡を動かす装置(写真の黄色の部分)のことを「赤道儀(せきどうぎ)」と呼びます。
ちなみに壊れた赤道儀の名前は、タカハシ社の EM-11 Temma2Jr. です(以後、単に EM11 と書きます)。
これが壊れると、主に次の2つのことができなくなります。
- 星の追尾
- 自動導入
星は日周運動をしていて、1時間に15度のペースで東から西へ動いていきますよね。
赤道儀は、この星の動きに合わせて望遠鏡を動かす機能があります。
これを「追尾」または「ガイド」などと呼びます。
また、星雲や星団など、見たい天体を指定すると、自動的にそれが見える方向に天体望遠鏡を向けてくれる機能もあります。
これを「自動導入」または「GOTO」などと呼びます。
こうした機能が使えなくなり、ただの重い台になってしまいました。
それ以来、天体観測や天体写真の撮影をしなくなってしまいました。
もちろん子供が生まれたり学習塾を始めたり、マイクラミングの開発や全国展開をしたり、何かと忙しくなったのも大きな理由でした。
どちらにしても天体観測をほとんどしなくなっていました。
また天体観測を始めるぞー
しかし、転機が訪れました。
昨年の紫金山・アトラス彗星です。
めっちゃ彗星の写真が撮りたい!
「天体観測をしたい」という思いが再び燃え出しました。
それで昨年から天体写真を少しだけ再開したのでした。
最初は、ただの三脚にカメラを載せて彗星の写真を撮りました。
もちろん、これだけでは星の追尾ができません。
日周運動ですぐに星が横にブレてしまい、満足した写真がなかなか撮れませんでした。
そこで小さな赤道儀を買いました。
Skywatcher社の Star Adventurer GTi という名前の赤道儀です(下の写真の白い部分)。
壊れた赤道儀に比べると、今回は4分の1以下の値段です。

この赤道儀は、軽い機材であれば星を追尾することができます。
たとえば小さな望遠鏡や、中型の望遠レンズを付けたカメラなど、小規模の機材ならOKです。
この赤道儀を使って、広角レンズや望遠レンズで撮影ができるようになりました。
彗星の写真は撮ることができました。→こちら
オリオン座の写真も撮りました。→こちら
天の川の写真も撮りました。 →こちら
しかし塾長の気持ちは収まりませんでした。
この赤道儀は、望遠鏡を動かせるほどのパワーがありません。
望遠鏡でなければ遠くの小さな天体の姿を写し出すことができません。
壊れた赤道儀のEM11と比べてしまうと、できることが限られます。
もっともっと遠くの天体を観測をしたい!!
さて、どうしたもんでしょう。
半信半疑でスタート
そんなわけで、天体観測を再開してから、赤道儀を修理すべきかどうか悩む日々が続きました。
ネットで赤道儀に関係するサイトや動画をよく見るようになりました。
すると、セレンディピティ効果というヤツですかね?
「赤道儀を自作したぜ!」という外国のスゴイ動画に出会いました。
それも1つだけではなく、3~4例くらいあるようでした。
例えば、Whyf16uyさんの動画です。
なかなかワイルドな工作です。
たとえばアルミ板にドリルでネジ穴をあける場面。
ドリルが斜めにズレて、途中からアルミ板の横へ穴が突き抜けちゃってます。
え、こんなんで作れるの!?
衝撃でした。
もしかしたら、自分にも作れるんじゃね?
金属工作の経験がない私にさえ、自信が湧いてきたほどです。
モーターを制御するためにプログラミングが必要みたいです。
プログラミングは得意なので問題ありません。
技術的な見通しが付きました。
なんだか、できる気がして来たのです。
修理するより、むしろ新しく作ってしまえ!
そう考えて、密かに赤道儀を自作するプロジェクトをスタートさせました。
ちょっと前まで赤道儀の自作なんて、それまで想像もできませんでした。
しかし、さらに調べて見ると、海外でも日本でも自作している人が多くいることが分かってきました。
おそらく、それができるだけの技術革新があったのでしょう。
コンピューターが小さく安価になったから、という理由もありますが、それだけではないようです。
どうやら、その肝になるのが「波動歯車」と呼ばれる装置。
実は、上の動画のタイトルに含まれる Harmonic Drive とは波動歯車のことです。
そこで、この波動歯車について色々と調べ、実際に注文しました。
届いたのがこれです(下の写真)。
要するに、これが上手く動くように赤道儀を設計します。

この油まみれの装置が波動歯車装置です。
モーターの回転速度を 1/100 に減速する代わりに、トルクを85~95倍に高めます(伝達ロスがあるので100倍にはなりません)。
星の動きはゆっくりなので、スピードよりも力(トルク)が大事!
これがあれば、小さなモーターでも重たい望遠鏡を振り回すことができます。
波動歯車装置の原理は1955年にアメリカで発明され、米国USM社が実現させました。そこでいち早く業務提携したのが、我らが日本の(株)ハーモニック・ドライブ・システムズ社でした(当時は長谷川歯車という社名)。そして両社が共同出資して製品化し、特許を取得したのが「ハーモニックドライブ」と呼ばれる装置です。
ただし、この装置の基本技術に関する特許(基本特許)は、けっこう前に有効期限が切れています。
それ以来、世界中の企業が研究開発に乗り出し、競争が激しくなっています。
なぜなら、ロボットや工作機械など様々な装置の部品として、とても有効な装置だからです。
天文業界では中国のZWO社が波動歯車装置を使った赤道儀を 2022年に発売しました。
当初、多くの天文ファンは、この全く新しい赤道儀に対して懐疑的でしたが、次第にその実力と評判が広まっていきました。
現在では複数のメーカーが波動歯車装置を使った赤道儀を販売しています。
ネットでも安い波動歯車装置が出回るようになり、手軽に購入できるようにもなりました。
そして、ついに、波動歯車装置を使った赤道儀の自作に挑戦する人たちが登場してきた、というワケです。
それが、ここ数年の動きです。
世界規模で見ると、技術革新のスピードが本当に加速しているのだと実感しますね。
なお「ハーモニックドライブ」という名前は商標登録されているため、(株)ハーモニック・ドライブ・システムズ社または同社と業務提携している会社の製品以外は名乗ることができません。
他社製品の場合は工業界の一般的な通名である「波動歯車装置」を使います。
海外のブログやYouTubeでは、波動歯車装置を使っているのに Harmonic Drive と表示していることがあるので要注意。
今回、私が購入したもの(上の写真)は中国の安価な任意製品なので波動歯車装置です。
2025年3月 モックアップの作成
さて、次は赤道儀の本体をどうやって作るか、が課題です。
頭で考えているだけでは何も進みません。
とは言え、いきなり作るのもリスクが大きいです。
そこで、まずは模型を作ることにしました。
イメージを具現化し、手に触れられるようにすれば、さらにイメージを細かくしていけます。
近くの文房具屋さん「ブンゾウ」へ行き、工作用の厚紙やボード、カッターなどを買ってきて作ったのがこれです。
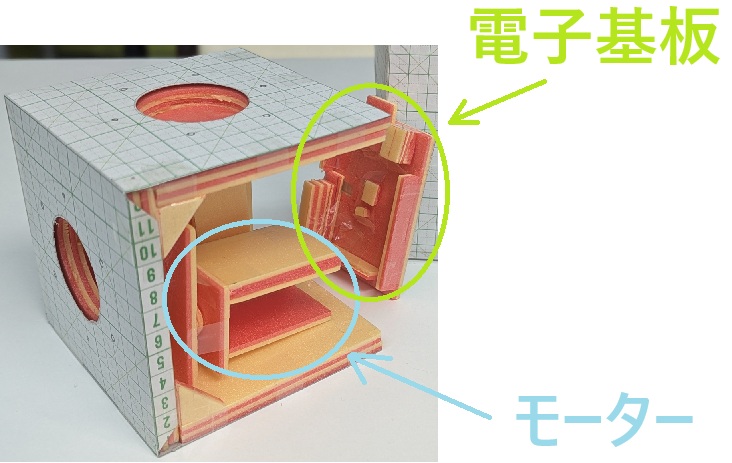
使用するモーターと電子基板を決めていたので、それが入る大きさの赤道儀にする方針です。
そのため、赤道儀の中に組み込むモーターや電子基板の模型も一緒に作り、寸法を確かめました。
最初はとりあえず赤道儀の本体は1辺14cmの立方体で作ってみました。
しかし、どう見ても大きすぎたので、12cmで作り直しました。
このように模型で確かめる作業は、プログラミング教室でも同じですね。
生徒たちはプログラムを組む前に、まず、建築したいものをマイクラで作ってみます。
つまりモックアップ(設計)を作るのですね。
それに座標を対応させてプログラミングをしていくわけです。
さて、上の写真のように、数回の試行錯誤を経て、およそ12㎝四方の大きさで赤道儀を作れそうだと分かりました。
これが最終的に 12.5cmになるのか11.5cmになるのか・・・
そういう細かい所は、ちゃんとした設計をして詰めていきます。
ここで、また1つ課題です。
立体構造の設計には、CADという設計アプリを使いこなす知識やスキルが必要です。
塾長は理学部数学科の出身ですから、こういう工学部の知識がありません。
そこで名古屋駅の本屋さん「ジュンク堂」へ行き、CADの本を買ってきました。
CADの勉強を始めました。
モーター制御についてもネットで調べて勉強を始めました。
2025年4月 モーター制御の実現
先に入手していたモーターと電子基板について、配線とプログラミングをしました。
CADの勉強を進めながら、それと平行して、できる作業も進めていきます。

モーターはステッパーモーター(ステッピングモーター)という特殊なモーターを使います。
ミニ四駆などで使うモーターとは違って、ただ電流を流しただけでは回転しません。
モールス信号のようにポツ、ポツ、とパルス状に電流を与えることで回転します。
1回のパルスで0.9度、つまり400回のパルスで1回転するようにできています。
こうした電流を制御するために、プログラミングが必要になります。
1秒間に400パルスを送れば1秒で1回転の速さで回転し、800パルスなら2回転、というようにして、スピードをコントロールします。
実際には、さらに精密な制御をするために「マイクロステップ」という技術を使ってパルスの間隔をもっと細分化します。
加えて、星の日周運動に合わせて一定の速度で回転させたり、自動導入に切り替えて加速させたり減速させたりする制御も必要です。
他にも様々な機能やモードの切り替えが必要になるわけですが、それをゼロからプログラミングするのは無理です。
それだけで何年もかかってしまいそうです。
実は、OnStepX という赤道儀専用のプログラムがインターネットでダウンロードできます。
プログラミング言語は Arduino用のプログラミング言語ですが、ほとんど C++ と同じです。
それを少しカスタマイズすれば、モーターを簡単に制御できるようになります。
OnStepX やその前身の OnStep は、世界中の天文ファンから支持されているオープンソースのプログラムです。
ネットで見る限り、2013年から公開されています。
実に12年間も、バグ修正や機能アップを繰り返しながら、多くのユーザーに支持され、鍛えられてきたプログラムです。
波動歯車装置が天文マニアの間で話題になるよりも、ずっと前からあるのですね。
これが無料で使えるなんて、世界には凄い人たちがいるものです。
赤道儀を自作する人が増えたのは、こうしたプログラムのオープンソース化という貢献が一番大きいのかもしれません。
こうした土壌があった上で、新しい機械技術が取り入れられてきたのでしょう。
私もいつか貢献できればよいなぁと思います。
さて、OnStepX のおかげでモーターを思い通りに回転させることに成功しました。
2025年5月 CADの設計
CADの勉強が、けっこう進みました。
FreeCAD というフリーソフトを使うことにして、その使い方も練習してきました。
ゴールデンウイークの連休を使って、いよいよ設計に挑戦!
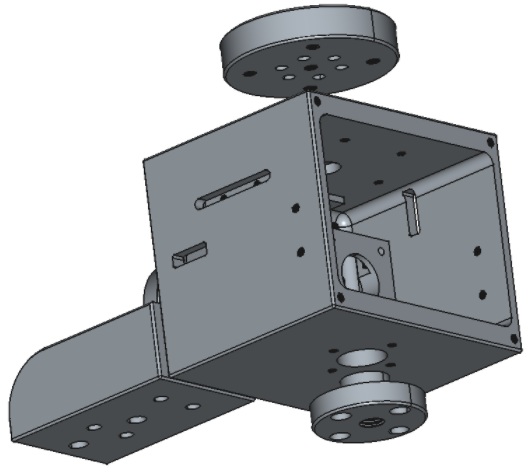
試行錯誤を繰り返し、なんとかそれらしい形ができました。
もっとも悩んだのはモーターの付け方です。
「サイズをコンパクトにまとめる」、かつ「強度を確保する」、かつ「モーターをしっかり固定する」、かつ「ベルトの張力を調整できるようにする」・・・
という条件です。
さらに途中でコストの観点「部品数を減らして安く抑えること」も重要だと気づきました。
これがけっこう破壊的で、ゼロから設計を見直す羽目になりました。
さらにさらに意外と盲点だったのが「組み立てが可能であること」、かつ「メンテナンスがしやすいこと」という点。
手が入らない、ドライバーが入らない、配線ができない、ではダメです。
最後に「拡張性があること」という条件も追加しました。
これらの条件をパズルのように重ね合わせ、すべてクリアするために、何度も何度も設計を繰り返しました。
また設計が進むほど構造が複雑になってくると、データ量が増え、コンピューターの動きがどんどん遅くなっていきます。
設計が進むほど、作業が進みにくくなります。
ちょっと進むとちょっと遅くなる。
まるで「アキレスと亀のパラドックス」のよう。
なかなかサクサクとは進みません。
手間も時間もかかりました。
たくさん作業したので、CADソフトはかなり使えるようになってきました。
このソフトから設計書をアウトプットすると、そのまま工場に「これを作ってください」と発注できるそうです。
あとは値段ですかね。
やすく仕上げてくれる企業を求めて、このあと世界中のサービスを検索することになります・・・。
さて、新しい知識を学ぶことや、新しいスキルを身を着けることは、何歳になっても楽しいものです。
塾長は昭和48年生まれ。52歳らしいですが、まだまだ勉強しています。
2025年6月 ジュラルミンの削り出し
設計したものを、どうやって実現させましょうか。
塾ですから、金属を加工できる工作機械はありません。
誰か作ってくれないかなぁ・・・と探していると、いくつか見つかりました。
日本の国内や海外のサービスをいくつか検討し、最終的には中国のサービスに決めました。
ネットで設計のデータや細かい指示を登録して発注できます。
注文後も技術的なことについて、何度かメールでやり取りをしました。
担当してくれたのはモニカさんという女性のエンジニアで、中国人ではないようです。
どうやらこの会社には世界中から優秀な人材が集まって来ているようです。
おかげで英語でメールをやり取りできました。
私は中国語ができないので助かりました。
それから3週間ほどすると、無事に部品が届きました。
紙で作った模型が、CADの設計になり、そしてついにアルミの部品になりました。
感動です!

材料はジュラルミンを指定しました。
飛行機に使われている強化型のアルミ合金です。
それをドリルで削り出して作ってもらいました。
削り出しの特長は「継ぎ目」がないこと。とても頑丈で美しい部品が作れます。
厚さは10㎜とし、市販品の赤道儀に比べ、2倍の厚みとしました。
とても頑丈なボディになったと思います。
むしろ頑丈にし過ぎたかもしれません。
これなら大きな望遠鏡を搭載しても大丈夫でしょう。
電子基板は本体のフタの裏に組付けます。
このフタの材料は白い樹脂を指定し、3Dプリンターで作ってもらいました。
さてさて、先に入手していた他の部品と合わせて、これで役者がそろいました。

2025年7月上旬 赤道儀の組み立て
部品を組み立て始めました。
ちゃんと設計ができているのか試される、緊張の一瞬です。
もしも少しでも寸法がズレていたら、ネジ穴がずれたり、ネジが入らなかったりして、組み立てることができません。
最初に波動歯車装置を本体に取り付けます。

おお、寸法ばっちりです。
本体の内部からはプーリー、ベルト、モーター、ベアリングも取り付けています。
次は望遠鏡を取り付ける台座と、日周運動の回転軸を受ける台座を取り付けます。

よしよし。
つぎは三脚につなげる台座を取り付けましょう。

クララが立った!
そういえば、この赤道儀の名前をまだ決めていませんでした・・・クララじゃありません。後で考えます。
背景は、めっちゃ教室です。
塾長の机が工場になってます。
生徒たちが来る前に、早く仕上げなければ・・・
最後は電子基板を組み込んだフタをはめます。

ふー。なんとか完成!
電源を入れて、動作確認も無事にクリアしました。
初めてのCAD設計。
こんなにも寸法通りにピッタリいくとは。
これまた感動です!
海の向こうの工場に設計データだけを送って作ってもらったのです。
それが海を渡って日本に到着し、そしてちゃんと組み上がる。
図面どおり、言葉どおりに作業ができ、誰がやっても同じアウトプットになること。
そのような再現性のある知識の伝達と、それによるアウトプット。
それらを総称して「技術」と呼びます。
なんか技術ってすごい!!
ちなみに「この人じゃなきゃできない」みたいなのは「技能」と呼びます。
真似をしたくても、なかなかできません。人によってアウトプットはバラバラ。
つまり再現性がありません。
よって「技術」と「技能」は違います。
もしも技術がなく技能しか無かったら、役割の分担ができません。
私が工場まで行って練習しないと部品ができないでしょう。
技術は世界を渡ります。
私が生徒たちに教えていることも同じ。
生徒たちには、
国語なら論理的に文脈をとらえる技術、
数学ならだれがやっても同じ計算結果になる技術、
理科や社会でも、そのような再現性のある知識について、
教えています。
逆に技能に関しては生徒それぞれの個性が出ます。
生徒の特性や得手不得手を見極めながら助言や伴走をします。
しかし代わってあげることはできません。
やるのは生徒、技能を高めるのは生徒自身にしかできません。
技術と技能の区別をしっかりつけて指導するよう心がけております。
2025年7月下旬 大失敗
本当にちゃんと動くことをテストしたいのですが、なかなか晴れません。
やっと晴れたとしても仕事との都合が合いません。
そんな中で、7月26日にチャンスがやってきました。
土曜日なので早く塾が終わります。
天気予報は晴れ。山よりは海の方がよく晴れるそうです。
今こそ行かねば!
と思い立ち、南知多の方へ出かけました。
夜釣りで有名な、とある港の広い駐車場に向かいます。
しかし、港に近づくにつれて賑わいが・・・あれ、こんなに人がいたっけ?
偶然にもその日は花火大会でした。
みんな楽しそう。
港は花火の打ち上げで封鎖されています。
夜空は花火できれいに彩られていて、天体観測どころではありません。
邪魔にならないように引き返し、別の観測場所を探しました。
「ここは電線が邪魔」
「ここは地面がぬかるんでる」
「ここは私有地?微妙だからやめとこう」
2時間以上ウロウロと彷徨いました。
そして日付が変わる少し前になって、ようやく観測できそうな場所を見つけました。
望遠鏡を組み立て、赤道儀の電源を入れました。
いよいよ試運転の開始です。

ところが・・・自動導入が上手くいきません。
最初は明るい星を導入してズレを補正するのですが、ズレどころが全く違う位置で止まります。
あれれ?
部屋でテストしたときは、それらしい方向を向いていたはずですが・・・ここまでズレるとは予想外。
焦りと暑さで、どっと汗が噴き出ました。
パソコンの画面をのぞき込み、何かおかしな設定がないか確認します。
そこへ、画面の明かりに釣られて虫がブンブン飛んできます。
うっとおしいです。
望遠鏡が目的の星まで移動する前に、赤道儀の動きが止まっているように見えます。
しかし、その原因がよく分かりません。
自動導入は諦めました。
それなら追尾はどうでしょうか。
追尾監視用のミニ望遠鏡に専用のCCDカメラを着け、CCDとパソコンをつなげます。
CCDに映る星が常に真ん中に来るよう、アプリが望遠鏡を制御します。
そのアプリからの指示に、赤道儀がうまく対応して動いてくれるのかをテストしました。
残念ながら、これもダメでした。
赤道儀は反応こそしているのですが、どんどんズレが大きくなっていき、正しく追尾ができていません。
写真撮影どころではありません。
その手前の段階で上手く動いていません。
何度も何度もトライ&エラーを繰り返しましたが、改善する気配がありません。
そうこうしている内に、どこからともなく、ニワトリの鳴く声が聞こえてきました。
見渡せば東の空が明るくなり始めています。
もう時間です。
テスト失敗・・・です。
諦めて帰ることにしました。
いったい何がどう悪かったのか・・・
悶々とした気持ちを引きずったまま家に帰りました。
シャワーを浴びて一息つくと、どっと疲れが出て来ました。
倒れるように昼まで寝ました。
昼食のとき、気持ちの落ち込みをごまかすように、妻に話しました。
私:「いやぁ、昨晩は大変だったよ。行ったら花火大会で港が封鎖されててさ。それで観測できるところを探して、2時間以上も知多半島を彷徨っちゃった。」
妻:「それで観測はできたの?」
私:「いや、まったく。ぜんぜん思ったように動かなくて、成果ゼロです。疲れただけでした。」
妻」「そんなに疲れてまでして、楽しいの?」
私:「ぜんぜん楽しくない。辛いです。」
とうとう本音が出てしまいました。
失敗の原因が分かっていません。
まだ悶々としていました。
よく考えたら、色々と調査不足でした。
オープンソースでネットからダウンロードしたプログラムの仕組みでさえ、よく分からないまま使っていました。
基盤の配線からプログラムの中身まで、ゼロから総点検することにしました。
2025年8月 ファーストライト
あれから1か月近く、ずっとプログラムの理解と点検を続けてきました。
失敗の原因は、どうやら電力不足だったということが分かりました。
モーターに投入する電流が小さすぎたようで、増強するようにプログラムを書き換えました。
また自宅でテストするときはコンセントから電源を取りますが、屋外ではバッテリーからです。
バッテリーからの電源供給は気を付けないと電流が細くなりがちです。
そこで赤道儀と他の機器で、電源を分けることにしました。
他にも細かい所や気になる所を修正しました。
新しく知識も増え、赤道儀にGPSや気象センサを追加するなどの機能アップも果たしました。
仕事に開発に、とても慌ただしい毎日を過ごしているうちに、
やがて、ほとんどの生徒たちが夏期講習を終え、夏休みも終わりが見えてきました。
思えば今年の8月は、ずっと天気が悪く、なかなか晴れてくれませんでした。
お盆休みに期待したペルセウス座流星群は、土砂降りの雨でした。
そして気が付けば、8月の最後の週末になっていました。
そろそろ晴れてくれないかな・・・天気予報を確認しました。
何ということでしょう。
今晩の天気予報は「快晴」。
夏期講習を頑張って来たご褒美なのでしょうか。
もう行くしかありません!
今度こそリベンジです!!
せっかくなので茶臼山高原まで足を延ばしました。

久しぶりの晴れ間とあって、現地では天体観測のファンたちが大集合していました。
茶臼山高原は、だいたい夜に来ると一人でポツンと天体観測を行うことになります。
鹿の鳴き声にビビりながら、クマの出現を警戒しながら、一人でせっせと観測します。
たまにドライブや走り屋の車が駐車場に立ち寄りますが、少し休憩すると、また直ぐに立ち去っていく、そういう場所です。
ところが、その日は何かの集会でもあるのかっていうくらいに駐車場がいっぱい。
しかも、どの車の横にも望遠鏡が並んでいました。
星まつり状態です。
何とか1台分のスペースを見つけ、車を滑り込ませました。
あと少し来るのが遅れていたら、駐車できなかったかもしれません。
さっそく赤道儀を設置し、望遠鏡を組み立てました。

そして、なんやかんやと調整をして、いよいよ撮影です。
ちゃんと精度よく星を追いかけてくれるでしょうか・・・。
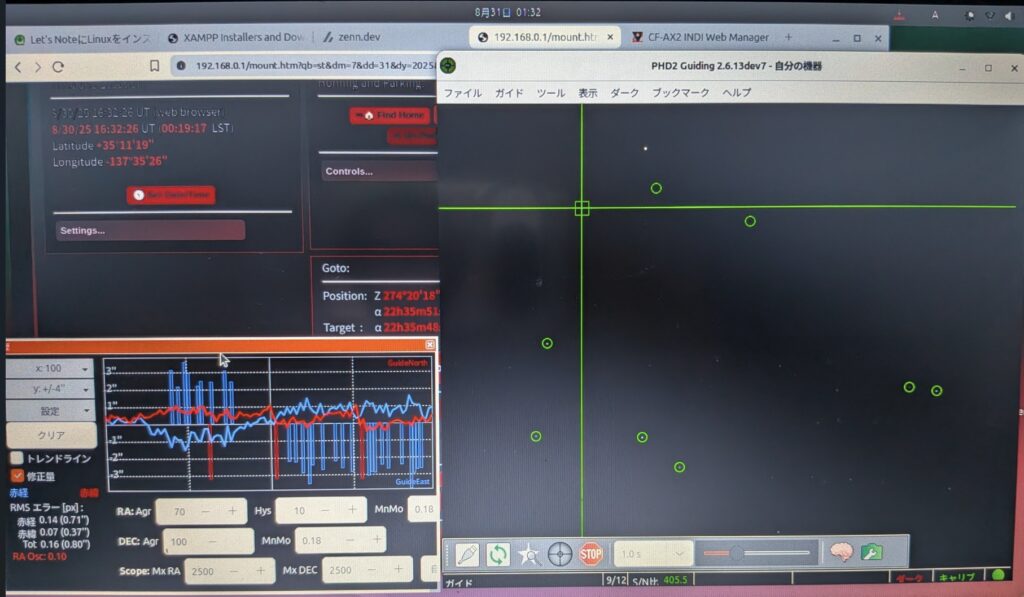
大丈夫そうです。
目標にしていた精度をクリアしました。
これなら撮影もうまくいっていることでしょう。
4、5時間いろいろと撮影や調査を続けていると、やがて東の空がほんの少し明るくなってきました。
気付けば深夜3時を過ぎていました。
そろそろ撤収しましょう。
しかし周囲の人たちは、まだまだ観測している様子でした。
でも塾長は日曜日しか休みがないため、無理はできません。
早めに撤収です。
2025年9月 天体写真の確認
さて日付が変わって9月になりました。
週末に撮影した天体写真。
ちゃんと撮れているでしょうか。
天体写真は、撮影してすぐに表示や印刷ができるわけではありません。
画像処理が必要です。
これがけっこう大変です。
上手な人がやると見違えるようにきれいな写真に仕上がりますが、塾長はまだまだ修行中の初心者です。
とは言え、とにかく確認するために処理を急ぎました。
最初に撮影したのは、子ぎつね座にある「あれい状星雲」(M27)です。

成功です!
ところで望遠鏡などの機材が初めて試験観測することを「ファーストライト」と呼ぶそうです。
特に天体写真の世界では、初めて撮影する天体写真のことを、そうに呼ぶことが多いです。
この赤道儀にとって、これがファーストライトになります。
上手くいって良かったです。
以前、この望遠鏡でM27を撮影したのは、2006年8月でした。
19年ぶりの撮影です。
もうそんなに月日が経ったのですね。
いろいろと忙しかったもんなぁ・・・。
次は、さんかく座にある渦巻銀河(M33)です。

良かった。これも撮れていました。
M33は17年ぶりの撮影です。
この銀河は私たちの天の川のお隣さんです。
といっても270万光年の彼方にあります。
この姿は270万年前、つまり旧石器時代が始まったばかりの頃の姿です。
最後はペガスス座になある遠くの銀河です。
NGC7331とスレファンの5つ子と呼ばれる銀河たちで、天文ファンの間では有名な絵になります。

これも17年ぶりの撮影です。
あの時よりもよく撮れました。
なんだか感動です。
右上の方にある、少し大きめの銀河がNGC7331です。
実は、この銀河は7月に超新星が見つかりました。
拡大したら写っていました!

縦横の黄色い線を延長して、それらが交わるあたりに星が1つ写っています。
それが超新星です。
2か月ちかうも経っているのに、まだ写るのですから、そうとう大きな爆発だったのでしょう。
実は、今回 NGC7331 を撮影対象に選んだのは、これを記録に残したかったからです。
この超新星はとても小さい映像なので、ダメもとで挑戦したのですが、写っていて良かったです。
超新星は、太陽の何十倍もあるような巨大な星が、一生の最後に起こす大爆発の姿です。
その中心ではブラックホールが誕生していることでしょう。
爆発している最中の姿ですから、そのうちに消えて見えなくなり、ブラックホールだけが残ります。
この銀河NGC7331は、約4000万光年の彼方にあります。
つまり4000万年前の姿です。
そのころの地球は、恐竜の白亜紀が終わって、次の古第三紀と呼ばれる時代です。
さて、この領域にはたくさんの銀河が写ります。
アノテーションというAI処理があって、天体の名前を表示させることができます。
やってみましょう。

文字が90度回転していますが、元の画像の向きの関係でそうなっています。
写真の左下に、多くの銀河が密集しています。
これが「ステファンの五つ子」と呼ばれれる銀河群です。
拡大して見ましょう。

(天体の向きが時計回りに90度回転していますが、これが元画像の向きなので気にしないでください)
これらの銀河は2億7000万光年かその前後くらいの彼方にあります。
地球では恐竜が誕生するよりも前の時代です。
それくらい昔の姿を、いま見ていることになります。
これらは互いに重力で引き合い、今まさに合体しようとしている最中です。
ただし、1つだけ仲間はずれがあります。
ひと周り大きいNGC7320だけは異なるグループです。
NGC7320は、たまたま同じ方向に重なって見えているだけで、実はずっと近く、2000万光年の距離にあります。
右上のNGC7331の4000万光年に比べると、その半分の距離しかありません。
それなのに小さいです。
NGC7320は、とても小さい銀河のようです。
さて、肝心の赤道儀の性能を振り返ってみます。
これはログを解析しました。
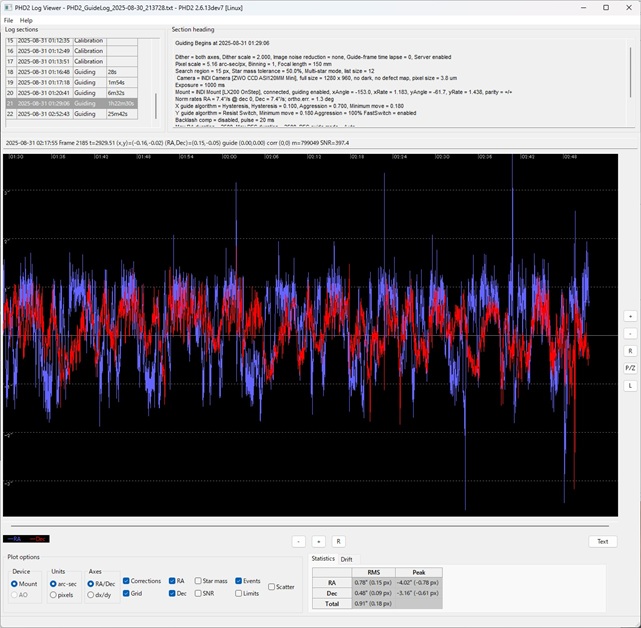
追尾の精度は 0.91秒 でした。
写真撮影に必要な「 1.20秒未満」を達成できました。
ハイブランドな市販品の赤道儀には及ばないものの、運用できるレベルです。
まずまずの「成功」と言ってよいでしょう。
7月のリベンジを果たすことができました。
まとめ
赤道儀の自作動画を始めて見たのがいつだったのか、記憶が定かではありません。
2024年12月ころだったのか、あるいは2025年になってからなのか、だいたいそのくらいのことだったと思います。
これから意を決して作り始めてから、あっという間に半年以上が経ちました。

望遠鏡を使った写真撮影ができるようになりました。
やっと少しばかりの達成感を味わうことができました。
過去を振り返ると、望遠鏡を使った写真撮影は、2012年6月6日の「金星の日面通過」が最後でした。

この撮影の後、どこかの時点で赤道儀 EM11 が壊れたのでしょう。
2014年10月8日の皆既月食の時に、電源を入れても正常に動作せず、それで故障と気が付きました。
それ以来、修理しようかどうか迷っている内に、仕事が忙しくなったりして10年以上の時間が過ぎてしまいました。

壊れた赤道儀 EM11 (上の写真)のメーカーは高橋製作所で、ブランド名は「TAKAHASHI」です。
日本が世界に誇る望遠鏡メーカーの1つで、この業界ではハイブランドの位置づけです。
しかし残念なことに2024年春ころ高橋製作所は赤道儀の製作と販売から撤退してしまいました。
部品在庫がある限り、まだ修理やメンテナンスはしてくれるそうですが、とてもショックでした。
このことも私が赤道儀を自作しようと思った要因の1つになっています。
さて、半年以上におよんだ「赤道儀の自作プロジェクト」でしたが、写真撮影ができるレベルに達しました。
目標とする性能を達成できたため、ひとまず「成功!」です。
今後も引き続き、使い勝手の向上と、さらなる精度アップに向け、一層の改善をしていく予定です。
使い勝手については、できればパソコン不要、スマホ1つで全て操作できるようにしようと思います。
精度アップについては、たとえば搭載しているモーターは、まだ本気を出していません。もっとパワーアップすれば応答性が上がり、さらに追尾精度が上がるでしょう。
ハンドコントローラなども追加したいですね。
夢は広がりますが、10月から別の仕事も入り、また忙しくなしそうです。
まぁ、ぼちぼちやっていきます。
データ
赤道儀のデータ
今回作成した赤道儀のスペックです。
- サイズ : 直方体部分: 100mm×118mm×100mm 、肉厚10㎜(ただし左右の側面のみ5mm)、マウントの全長: 未測定
- 素材 : ジュラルミン(A7075)削り出し
- 重量 : マウント本体 5.2Kg(ウェイトシャフトやウェイトは含まず)
- モーター: RA/DEC 共通: Nema17 0.9 deg/step 46Ncm 2.0A 1.5Ω
- 減速比 : RA/DEC 共通: 300:1 (波動歯車=17型 100:1 および プーリー&ベルト=60:20)
- 制御 : OnStepX Ver. 10.26.a6 Wifi Serial 9600bps on USB GPS搭載、気象センサ(気温、気圧、湿度)搭載
- 搭載可能重量: 未測定(カウンターウェイト必須で 25Kg 以上が目標)
- その他 :
- ウェイトシャフト: アタッチメント式で、タカハシ、ビクセン、Skywathcer 各社のものを取り付け可能(今回はタカハシを利用)
- 左右の側面: ビクセン小型アリミゾを装着できるネジ穴(ASI Air などを取り付け可能)
- 左右の背面: Sky Watcher CQ350PRO用極軸望遠鏡を取り付けるネジ穴(ネジ穴が合えば他の極軸望遠鏡の装着も可能)

撮影の共通データ
8月のファーストライトで撮影し、9月に画像処理をした写真のデータです。
- カメラ CANON EOS60Da(EOS60Dの天体写真専用モデル)、ISO2000、LPS-P2フィルタ内蔵
- 望遠鏡 Vixen R200SS + コマコレクターPH
- 赤道儀 ゼロ(自作の零号機、本体重量5.2Kg ジュラルミン製、OnStepX による制御)
- 三脚 INNOREL RT90C
- 電源 DABBSSON 600L(半固体電池 768Wh, AC出力600W(純正弦波, 瞬間1200W, Boost 900W))
- ガイド ZWO 30F5ミニスガイドコープ、 ZWO ASI120MM、PHD2 + INDI drivers on Ubunt24.04
- 処理 Siril 1.4.0-beta3 による画像処理およびアノテーション、ペイントによるトリミングおよび名入れ
- 日時 2025年8月30日(土) ~ 31日(日) 未明
- 場所 茶臼山高原道路 面の木駐車場 標高約1,100m 気温19℃
M27(こぎつね座 あれい状星雲)
- 日時 8/30(土) 21:55 ~ 22:37
- 露出 約26分 (299秒×5枚 + 47秒 + 49秒)
M33(さんかく座 渦巻銀河)
- 日時 8/30(土) 23:05 ~ 8/31(日) 00:46
- 露出 約72分 (299秒×14枚 + 122秒)
NGC7331とステファンの五つ子(ペガスス座の銀河群)
- 日時 8/31(日) 01:25 ~ 02:52
- 露出 約81分 (299秒×15 + 64秒 + 305秒)
ダークフレーム
帰宅しながら撮影したため温度がバラバラ・・・。
- 19℃ 299秒×5枚
- 22℃ 299秒×5枚
- 27℃ 299秒×5枚
以上です!
進学実績
卒塾生(進路が確定するまで在籍していた生徒)が入学した学校の一覧です。
ちなみに合格実績だけであれば更に多岐・多数にわたります。生徒が入学しなかった学校名は公開しておりません。
国公立大学
名古屋大学、千葉大学、滋賀大学、愛知県立大学、鹿児島大学
私立大学
中央大学、南山大学、名城大学、中京大学、中部大学、愛知淑徳大学、椙山女学園大学、愛知大学、愛知学院大学、愛知東邦大学、愛知工業大学、同朋大学、帝京大学、藤田保健衛生大学、日本福祉大学
公立高校
菊里高校、名東高校、昭和高校、松陰高校、天白高校、愛知教育大学附属高校、名古屋西高校、熱田高校、緑高校、日進西高校、豊明高校、東郷高校、山田高校、鳴海高校、三好高校、惟信高校、日進高校、守山高校、愛知総合工科高校、愛知商業高校、名古屋商業高校、若宮商業高校、名古屋市工芸高校、桜台高校、名南工業高校、菰野高校(三重)
私立高校
愛知高校、中京大中京高校、愛工大名電高校、星城高校、東邦高校、桜花学園高校、東海学園高校、名経高蔵高校、栄徳高校、名古屋女子高校、中部第一高校、名古屋大谷高校、至学館高校、聖カピタニオ高校、享栄高校、菊華高校、黎明高校、愛知みずほ高校、豊田大谷高校、杜若高校、大同高校、愛産大工業高校、愛知工業高校、名古屋工業高校、黎明高校、岡崎城西高校、大垣日大高校
(番外編)学年1位または成績優秀者を輩出した高校
天白高校、日進西高校、愛工大名電高校、名古屋大谷高校
※ 成績優秀者・・・成績が学年トップクラスで、なおかつ卒業生代表などに選ばれた生徒
名古屋市天白区の植田で塾を探すなら個別指導のヒーローズ!!
★ 直接のお問い合わせ ★
――――――――――――――――――――――
個別指導ヒーローズ 植田一本松校
〒468-0009
名古屋市天白区元植田1-202 金光ビル2F
TEL:052-893-9759
教室の様子(360度カメラ) http://urx.blue/HCgL