塾長です。
10月はレモン彗星とスワン彗星を追いかけてきました。
それで今年の彗星祭りは終わりかと思っていたのですが・・・
なんと、11月も2つの彗星が注目されていることが分かりました。
しかも1つは太陽系の外から飛来しているとか。
なんでもエイリアンの宇宙船だと疑う人がいるなど、世間を騒がせているそうですよ。
さっそく観測しきました。
2つのアトラス彗星
11月中旬の深夜に日本から見える彗星は2つ。
- C/2025 K1 (ATLAS) 彗星
- 3I/ATLAS 彗星 (太陽系の外からやって来た恒星間彗星。恒星間彗星は史上3番目の発見)
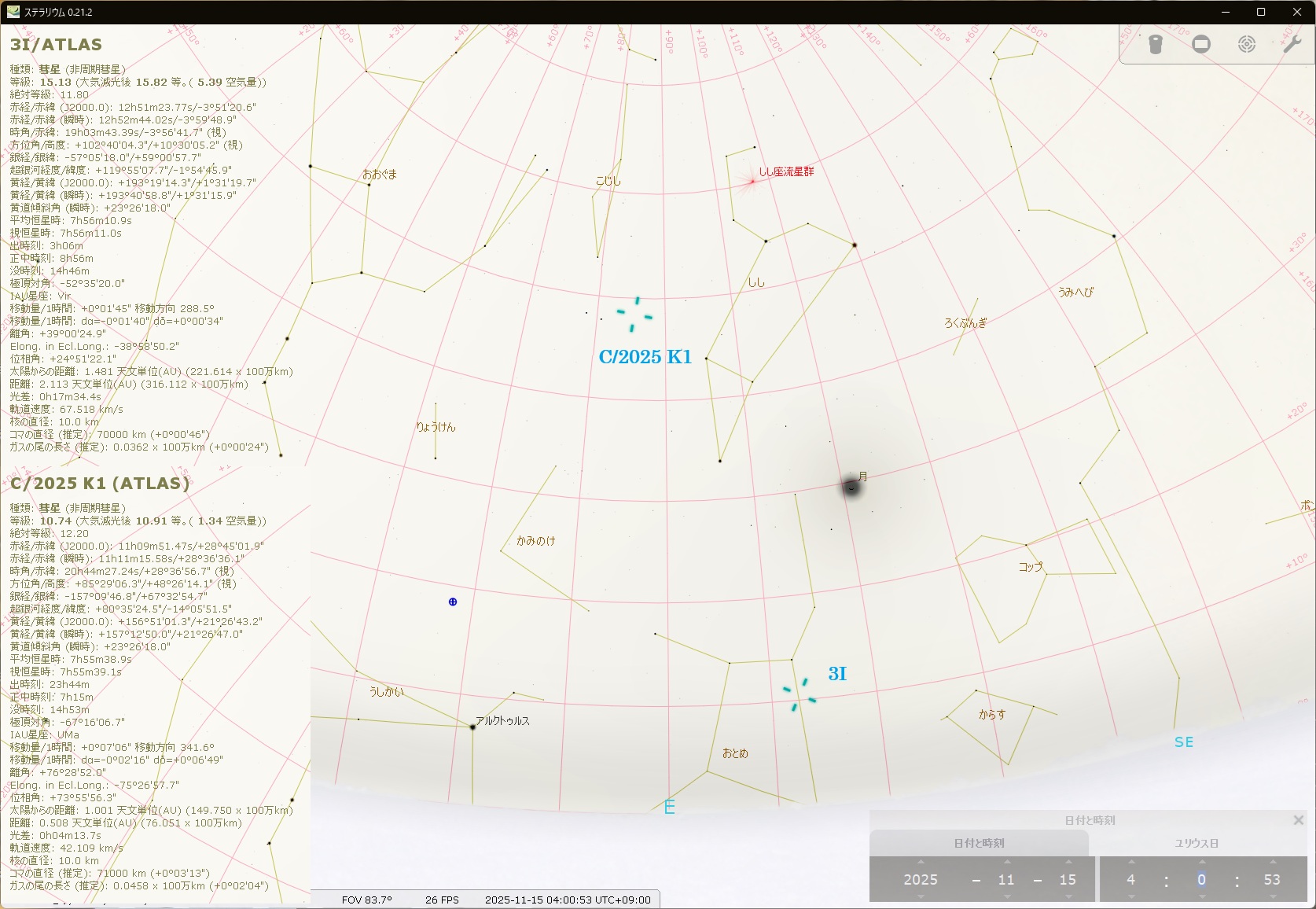
2025年11月15日AM4時ころの位置は、下図の通りです。
どちらも望遠鏡でやっと見えるか見えないか、というくらい暗くて小さいです。
なお図はフリーソフト「ステラリウム」の画面を使って作成しました。
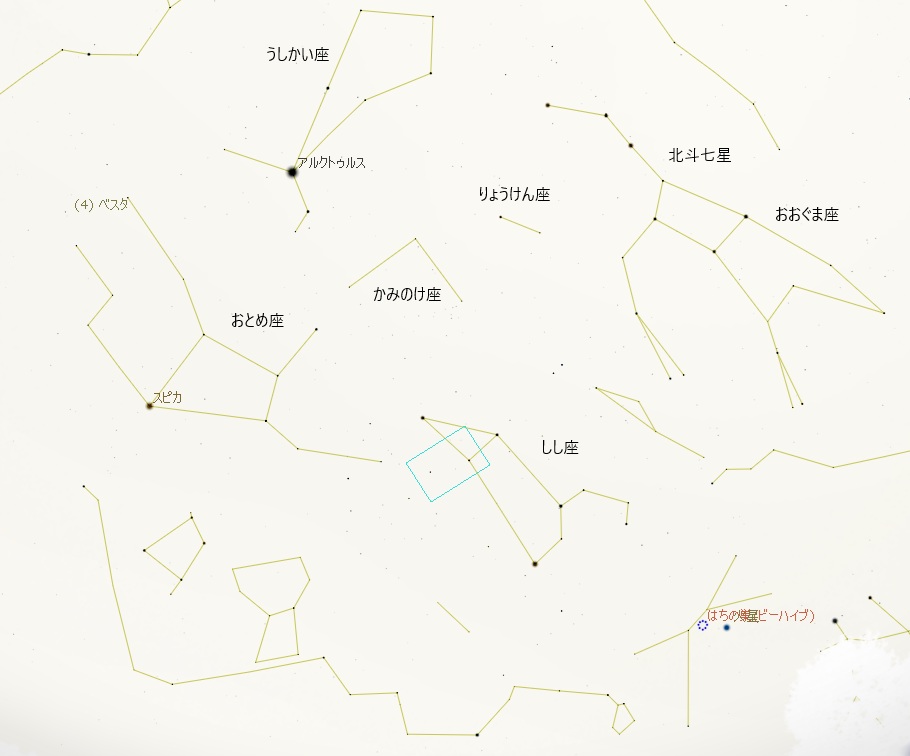
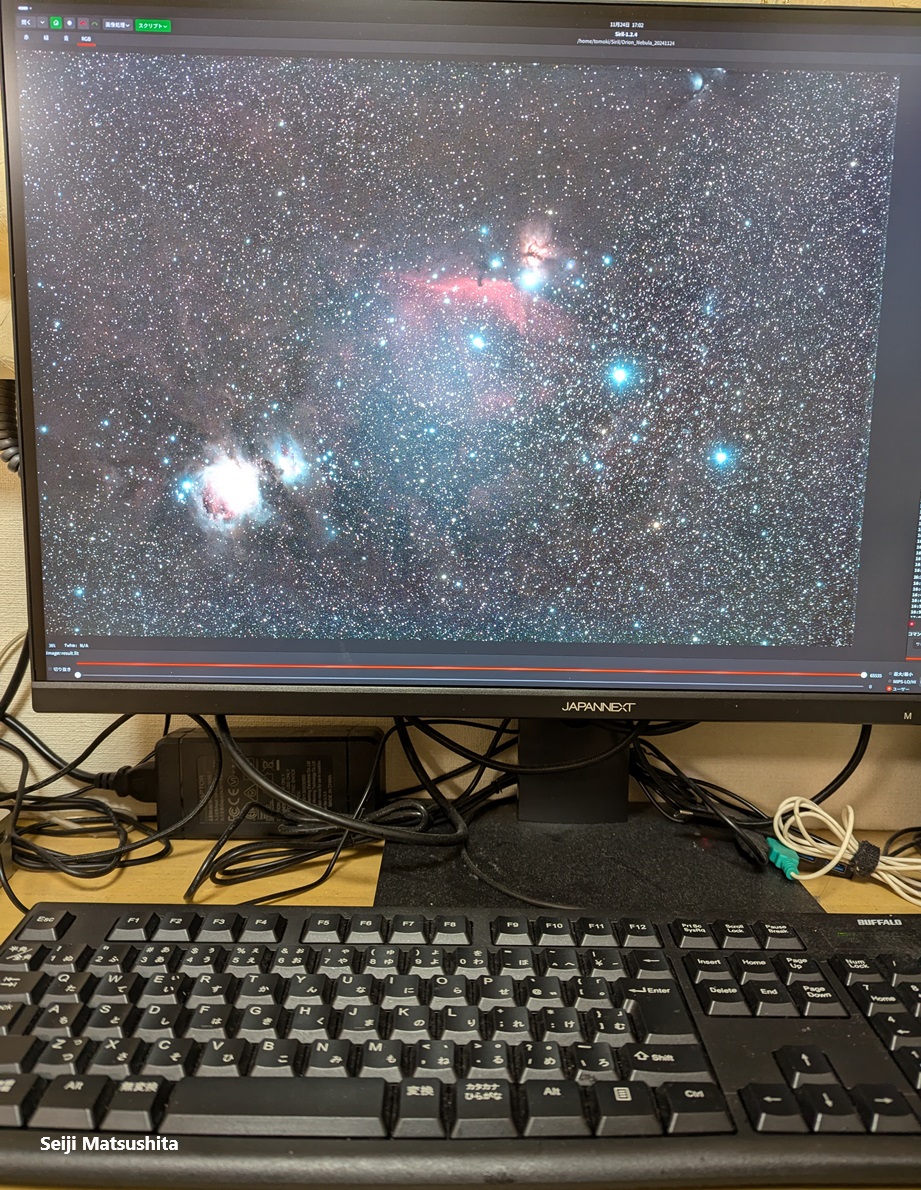
下の写真は当日の明け方、北東の夜空です(観測の終わりごろに撮影)。
2つの彗星がある方面をスマホで撮影したのですが、街が明るいので小さい星は写ってくれません。
上の星図と見比べて、およその彗星の位置を水色でマークしてみました。

写真のとおり名古屋市郊外なので星はそれほど見えません。
周囲の街明かりで空が照らされ、暗い星はかき消されてしまいます。
写真を撮るときには、「街の明かりをカットし、星の光だけをよく通す」という特殊なフィルターを使って撮影します。
ところで、2つの彗星の名前には、どちらもATLAS(アトラス)が含まれています。
昨年の「紫金山・アトラス彗星」にも「アトラス」がついていました。
アトラスとは、NASAとハワイ大学が運用している小惑星地球衝突最終警報システム(Asteroid Terrestrial-impact Last-alert System) のことです。
地球に衝突しそうな隕石がないかどうか、いつも監視しているため、そのついでに彗星を多く発見します。
このシステムが発見した彗星には ATLAS の名が付く、というわけです。
C/2025 K1 彗星と遠くの銀河たち
夜12時前に機材のセットをひととおり終えました。
他の天体を撮影しながら、待つこと2時間・・・
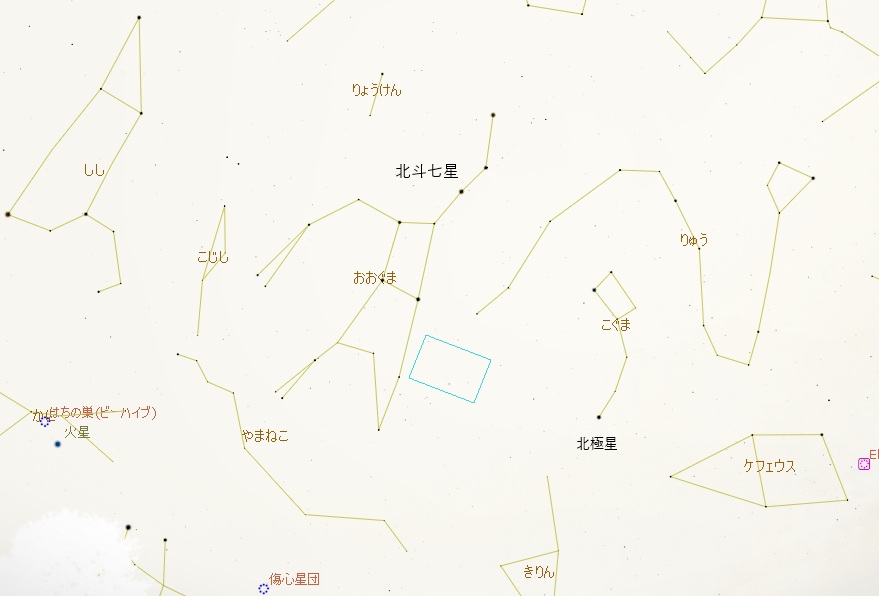
最初に昇って来たのは、C/2025 K1 (ATLAS) 彗星です。
ステラリウムには事前に彗星の軌道データを追加しておきました。
ステラリウムで望遠鏡の視野をシミュレーションすると、彗星の近くに銀河が複数があるようです。
この場所は、おおぐま座の端っこです。
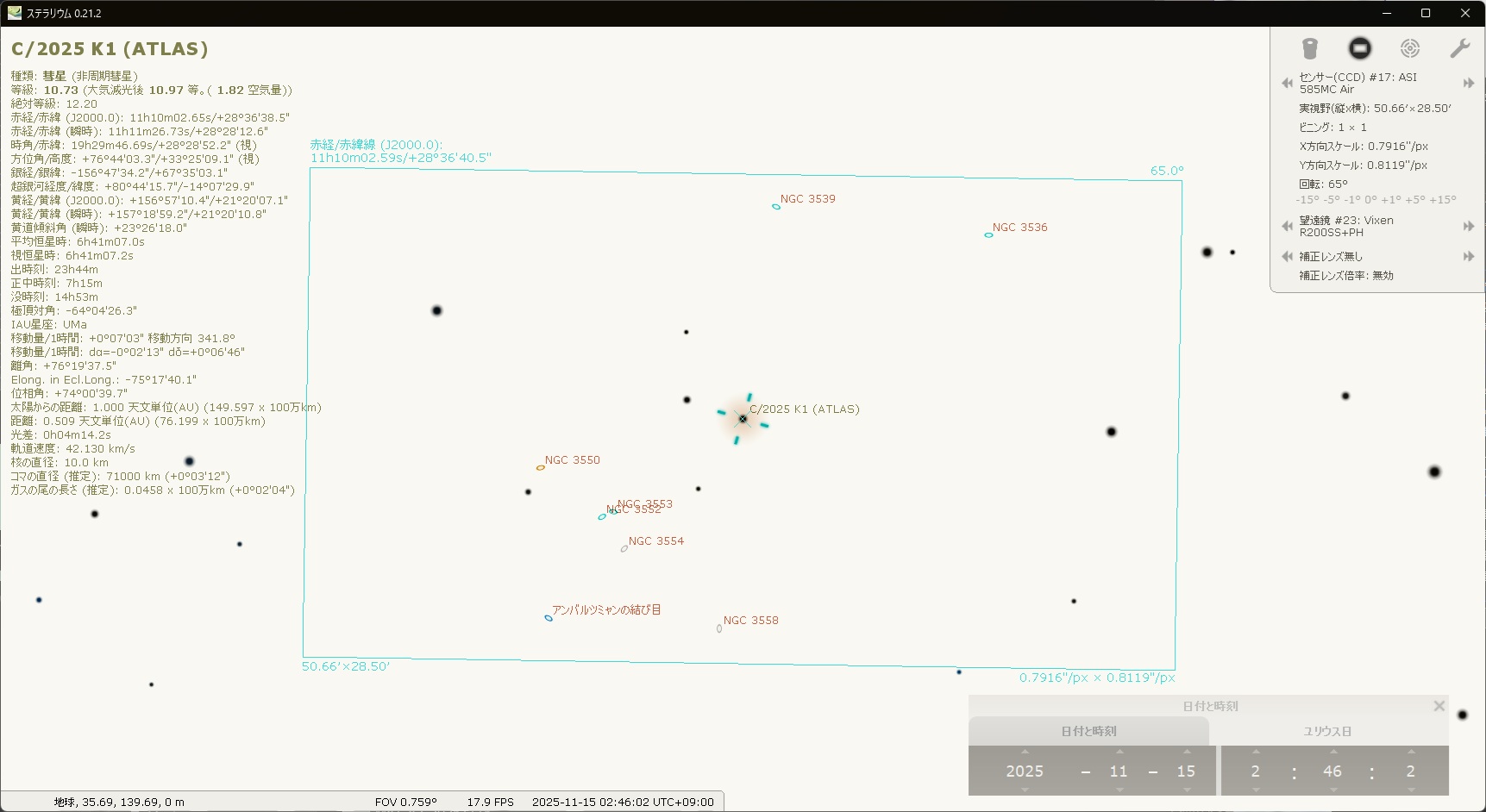
これらの銀河と彗星を一緒にねらって撮影したのが下の写真です。
この1枚を撮影するのに3分間かけています(露出60秒×3枚)。
彗星の動きはとても速く、この3分の間にも動いていきます。
彗星の中心部が点ではなく、横にズレた線になっているのは、それだけ彗星が動いたからです。

よく見ると彗星の下に淡い斑点がいくつか写っています。
これは銀河でしょうか、それともボケた星やノイズでしょうか。
いったい何が写っているのかを、コンピューターに判定させたのが下の写真です。

やった、銀河でした!
コンピューターが判定した上の画像について、少し説明します。
いくつかの星が赤く色づけされています。
これはコンピューターが星の配置パターンを認識するために使った星たちです。
星の配置パターンをデーターベースと照合し、望遠鏡の向きや視野の角度などを自動的に判定しています。
緑色の円で囲まれているのが遠くの銀河です。
7つの銀河が検出されたようですね。緑の字で銀河名も表示されています。
これら7つは Abell 1185 という銀河団です。
何兆倍という距離の差!
もっとも大きく写っていた銀河が NGC3550 です。
距離は4億光年~4億9千万光年。
つまり4億年以上前の姿を見ているわけです。
4億年前の地球といえば、植物が陸上に進出し始めたころ。
動物はまだ海の中で暮らしていました。
C/2025 K1 (ATLAS) 彗星までの距離は、約4光分(光の速さで4分弱、約6800万キロメートル)。
一緒に写っている銀河群までの距離は、約4億光年以上(光の速さで4億年以上)。
50兆倍以上も距離のちがう天体が1枚の写真に収まっているのは、なんとも不思議な光景です。
別の星から来た 3Iアトラス彗星
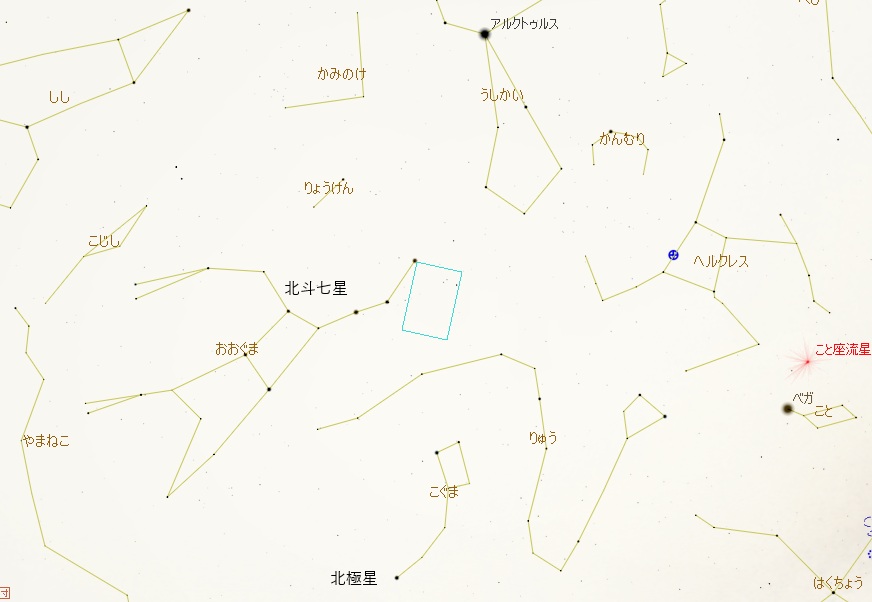
明け方の4時を過ぎると 3I/ATLAS 彗星も昇ってきました。
おとめ座の1等星「スピカ」は、また地平線付近ですが、その上の方に彗星があるはずです。
下の図はステラリウムでシミュレーションした望遠鏡の視野です。
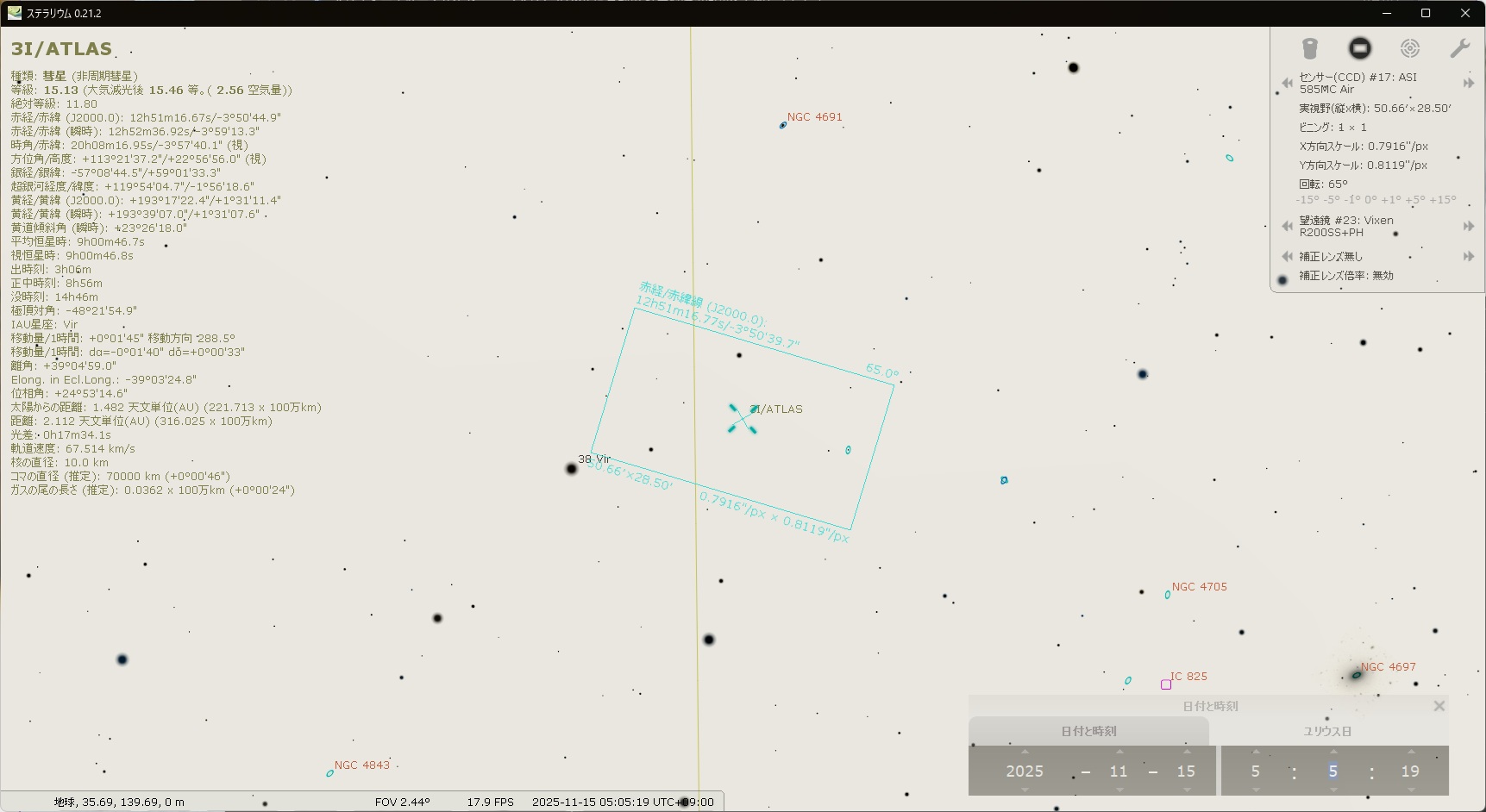
とくに目立つ星や天体がない領域です。
こういう場所にある天体は見つけるのが大変なんですよね。
もしも望遠鏡に自動導入の機能がなかったら、見つけることができなかったかもしれません。
昔は彗星を探しているうちに夜が明けてしまった、などという経験が何度かありました。
文明の利器で難なく導入に成功し、撮影しました。
こちらは10分露出しました(60秒×10枚)。

写真の中央に、ぼうっとした天体があります。
それが 3I/ATLAS 彗星です。
この彗星までの距離は約3億Km。
地球と太陽の距離が1億5000万Kmですから、その約2倍です。
上の C/2025 K1 (ATLAS) 彗星と比べると4~5倍くらい遠いのですから、暗くて当然でしょう。
彗星らしく尾を引いている姿を期待しましたが、尾は写ってくれませんでした。
この彗星は、その姿が日々変わると言われており、尾がある日もあれば、ない日もあります。
あるいは、この日は空の透明度が悪かったため、単に暗い尾まで写せなかっただけかもしれません。
彗星の軌道がおかしい
3I/ATLAS 彗星は2025年7月1日に発見され、世界中の天文学者の注目の的となりました。
軌道が楕円ではなく双曲線だと判明するや否や、すぐにハッブル宇宙望遠鏡による追加観測が行われました。
予約でいっぱいの宇宙望遠鏡が使われたということは、それだけ重要な発見だったということです。
なぜなら、この彗星が太陽系の外からやってきた天体だと判明したからです。
NASAは 3I/ATLAS 彗星の専用サイトを設けて、観測の詳細を公開しています。
その一部を紹介しましょう・・・
ハッブル宇宙望遠鏡が7月21日に撮影した映像です(NASAのサイトのリンクを埋込表示)。
少し尾が確認できます。
NASAが発表している、この彗星の軌道です(NASAのサイトのリンクを埋込表示)。
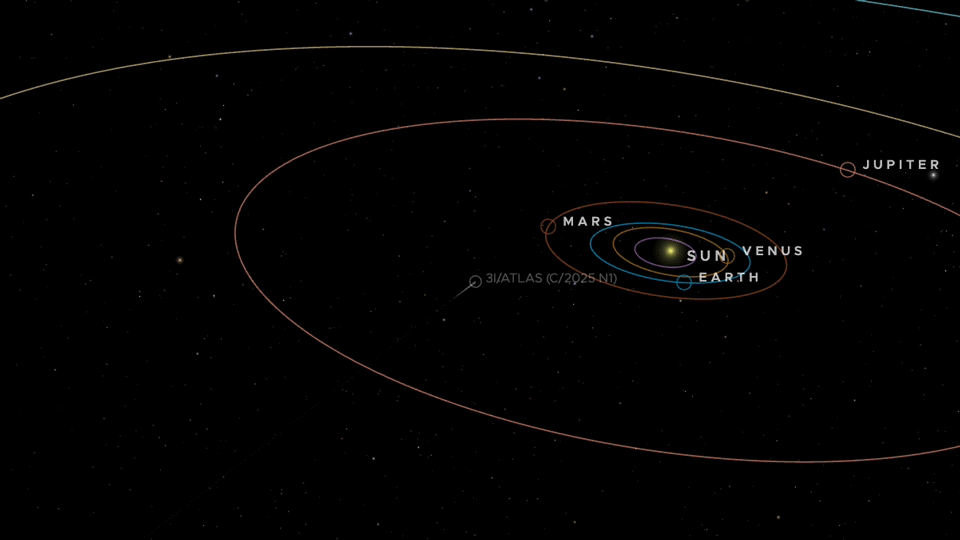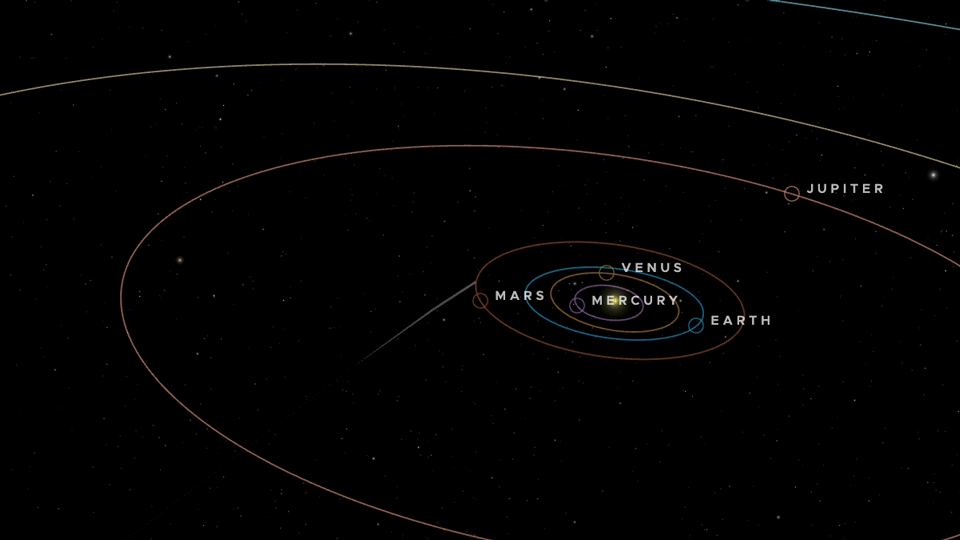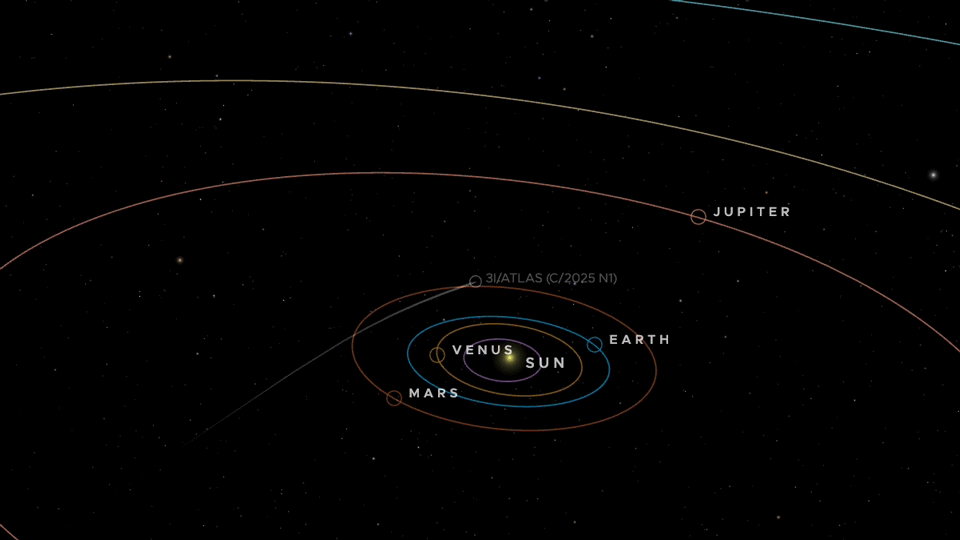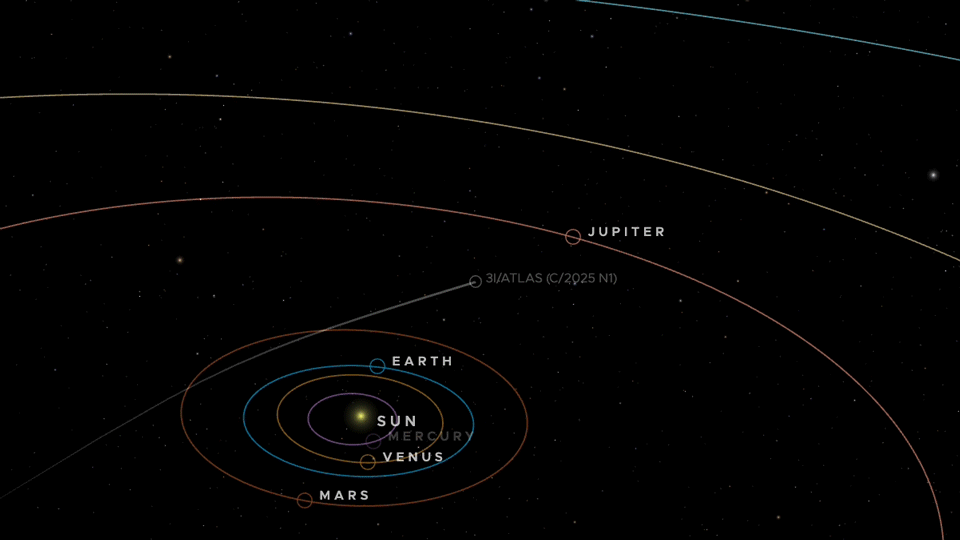
火星軌道の内側を通り抜け、地球には12月19日ころに最接近します。
そのあと木星方面へ進んでいきます。
そのまま太陽系を後にして、やがて別の星へ旅立っていくようです。
NASAによれば、この彗星は普通の彗星と比べて、スピードがとても速いそうです。
発見当時の時点で秒速58Kmという猛スピード!
太陽に最接近する10月29日には秒速68Kmに達すると見積もられました。
ちなみに地球を出発点とした脱出速度は、
- 太陽系からの脱出速度: 秒速16.7Km
- 銀河系からの脱出速度: 秒速300Km
らしいです。
※ 脱出速度の式 $ v=\sqrt{\frac{2GM}{R}} $ は高2物理で習います。
太陽の重力を振り切り、太陽系を抜け、また別の星まで飛んでいくでしょう。
わずか1年たらず、2026年のうちに太陽系から脱出するようです。
例えば1977年に打ち上げられた探査機「ボイジャー1号」のスピードは秒速17Km。
太陽系を脱出するのに約40年かかっています。
それに比べると3I/ATLASがどれだけ爆速であるかが想像できます。
また電波観測から、この彗星が太陽系の外で作られたことが示唆されています。
その成分から、太陽系ができるよりも前、もっとずっと昔から存在していた可能性も示唆されています。
銀河系内の恒星をいくつか訪れるたびに尾をなびかせ、質量を失い、やがて宇宙の塵になるのかもしれません。
実は、このような天体は初めてではありません。
太陽系の外から飛来してきた天体を人類が観測するのは、これで3つ目。
たった3つですから、とても珍しい天体。
天文ファンなら、これだけでご飯3杯はいけます。
なお、彗星の名前 3I/ATLAS のI は Interstellar 「恒星間」の I です。
広大な宇宙の中で、星と星の間を旅する彗星であることから、このような記号が付いています。
3I とは「3番目に発見された恒星間の天体」という意味になります。
3Iアトラス彗星は宇宙船かもしれない?
3I/ATLAS 彗星は珍しい、というだけではありません。
実は、想定外の加速をしていたことが観測されています。
彗星ですから、太陽の重力で加速するのは当然なのですが、
どうも、それだけでは説明のつかない加速をしていたようです。
彗星の表面は、太陽光で物質が蒸発してガスを噴射します。
そのガスがロケット噴射のような役割をして加速した、ということが考えられます。
しかし、その仮説で噴射されたガスの総量を計算すると、彗星自身の重さを超えてしまいました。
つまりガスの噴射では説明できません。
また、太陽系の外から飛来した彗星であれば、惑星の公転軌道面とは大きく異なる角度でやってくるのが普通です。
わざわざ太陽系の公転軌道面に沿ってやってくる確率は低く、少ない事例の中で、そういう天体に出会える確率はとても低いはず。
それなのに、たった3つ目の発見にして、もう出くわしたともなれば、本当に偶然の中の偶然でしょう。
つまり、
ロケット並みに強力な加速ができて、
ご丁寧に太陽系の公転面に合わせて侵入して来た、
ということで、そんな稀有な天体なんて、なかなか見られません。
それだけに、
きっとロケット噴射をしたに違いない!
宇宙船が太陽系を観察しにやって来たのだ!
そんな憶測が飛び交っています。
果たして真相はいかに!?
実は、このような憶測でお祭り騒ぎになるのは、今回が初めてではありません。
最初に発見された恒星間天体「オウムアムア」が 2017年に飛来した時も、謎の加速が観測されました。
さらにオウムアムアは極端に細長い形をしていたため、それこそロケットだと思われたのでした。
ちなみに、オウムアムアのNASA専用サイトもあります。
その後ほどなくして、オウムアムアの謎の加速を説明できる理論が発表されたのでした。
3I/ATLAS 彗星の加速も、いつか説明できる理論が登場するでしょう。
※NASAは11月19日に正式見解を発表し 3I/ATLASと知的生命体との関係を否定しています
北斗七星の周りには銀河がいっぱい
さて、無事に2つの彗星を写真に収めることができました。
実は、2つの彗星を待っている間とても暇でした。
この日の最低気温は6℃。そんな寒い中、ただ待っているだけというのは辛すぎます。
幸い、2つの彗星の近くには、おおぐま座の北斗七星があります。

北斗七星のまわりには、たくさんの銀河が観測できます。
特に早くから昇って来るのが M81とM82のペアです。
そこで彗星を待っている間、ひたすらM81とM82を撮影しました。
それが下の写真です。

右上の銀河がM81です。ボーデの銀河とも呼ばれ、きれいな渦巻き銀河です。
左下の銀河はM82です。葉巻銀河とも呼ばれ、構造が不規則な銀河です。
この2つの銀河については、以前こちらのブログでも紹介しました。
詳細は4月29日のブログ「【天体観測】天の川の写真を撮って来たよ」をご覧ください。
あとがき
仕事の都合がつき、なおかつ晴れる日ともなると、観測できるチャンスは本当に少ないものです。
今回は塾の仕事を終えてから観測に出かけたため、遠くまで出かけることができませんでした。
名古屋市近郊とはいえ、観測をスタートできたのは夜12時頃からでした。
秋と言えば、スッキリ晴れた天気に夕焼け、というイメージですが、今年はどうも違います。
空気中の水蒸気が多く、空気が霞んでいます。
この日も透明度が悪く、4等星がやっと見える程度でした。
秋の夜空とは思えない、スッキリしない夜空でした。
それでも話題の彗星を観測できたのは幸運でした。
街の明かりに邪魔されて、ほとんどの星は見えませんが、
特殊なフィルターを使って撮影したため、なんとか天体の姿を映し出すことができました。
とはいえ、フィルターも万能ではありません。
街の光と一緒に天体の光もカットしますから、どうしても露出が不足しがちになります。
銀河のように天の中で動かない天体であれば、露出を増やせますが、
彗星のように天の中を動いていく天体となれば、それができません。
やはり山奥のきれいな星空が恋しいです。
とはいえ、山はクマが出るし、冬は雪で閉鎖される所も多いです。
自然の変化に対して、技術だけでは全てを解決できません。
正常な自然の状態に戻って欲しいものです。
撮影データ
撮影の共通データ
写真や機材の共通データです。
- 赤道儀 ゼロ(自作の零号機、本体重量5.2Kg ジュラルミン製、OnStepX による制御)
- 三脚 INNOREL RT90C
- 電源 DABBSSON 600L(半固体電池 768Wh, AC出力600W(純正弦波, 瞬間1200W, Boost 900W))
- ガイド ZWO 30F5ミニスガイドコープ、 ZWO ASI120MM、ZWO ASI-Air mini
- 画像処理 Siril 1.4.0-beta3 による画像処理、必要に応じてペイントによるトリミング・回転・解説記入・名入れ
観測風景 しし座と2つのアトラス彗星
- 日時 11/15(土) 04:36
- 場所 日進市内の田園地帯
- カメラ Google Pixel 10
- 露出 1/3秒(夜景モード)
観測風景 北斗七星と3Iアトラス彗星
- 日時 11/15(土) 04:41
- 場所 日進市内の田園地帯
- カメラ Google Pixel 10
- 露出 1/3秒(夜景モード)
C/2025 K1 彗星(素の写真と解説入りの2枚)
- 日時 11/15(土) 02:37 – 02:40
- 場所 日進市内の田園地帯
- カメラ ZWO ASI585MC Pro、Gain200、-10℃、Antlia Quad Band Anti Light Polutionフィルタ
- 望遠鏡 Vixen R200SS + コマコレクターPH
- 露出 3分(60秒×3枚)、トリミング
- 解説 Siril によるアノテーション(銀河の検出と名入れ処理)
3Iアトラス彗星
- 日時 11/15(土) 05:06 – 05:15
- 場所 日進市内の田園地帯
- カメラ ZWO ASI585MC Pro、Gain200、-10℃、Antlia Quad Band Anti Light Polutionフィルタ
- 望遠鏡 Vixen R200SS + コマコレクターPH
- 露出 10分(60秒×10枚)、トリミング
M81とM82
- 日時 11/15(土) 00:39 – 02:24, 02:53 – 04:08
- 場所 愛知池
- カメラ ZWO ASI585MC Pro、Gain200、-10℃、Antlia Quad Band Anti Light Polutionフィルタ
- 望遠鏡 Vixen R200SS + コマコレクターPH
- 露出 2時間27分(60秒×147枚)
以上です!
進学実績
卒塾生(進路が確定するまで在籍していた生徒)が入学した学校の一覧です。
ちなみに合格実績だけであれば更に多岐・多数にわたります。生徒が入学しなかった学校名は公開しておりません。
国公立大学
名古屋大学、千葉大学、滋賀大学、愛知県立大学、鹿児島大学
私立大学
中央大学、南山大学、名城大学、中京大学、中部大学、愛知淑徳大学、椙山女学園大学、愛知大学、愛知学院大学、愛知東邦大学、愛知工業大学、同朋大学、帝京大学、藤田保健衛生大学、日本福祉大学
公立高校
菊里高校、名東高校、昭和高校、松陰高校、天白高校、愛知教育大学附属高校、名古屋西高校、熱田高校、緑高校、日進西高校、豊明高校、東郷高校、山田高校、鳴海高校、三好高校、惟信高校、日進高校、守山高校、愛知総合工科高校、愛知商業高校、名古屋商業高校、若宮商業高校、名古屋市工芸高校、桜台高校、名南工業高校、菰野高校(三重)
私立高校
愛知高校、中京大中京高校、愛工大名電高校、星城高校、東邦高校、桜花学園高校、東海学園高校、名経高蔵高校、栄徳高校、名古屋女子高校、中部第一高校、名古屋大谷高校、至学館高校、聖カピタニオ高校、享栄高校、菊華高校、黎明高校、愛知みずほ高校、豊田大谷高校、杜若高校、大同高校、愛産大工業高校、愛知工業高校、名古屋工業高校、黎明高校、岡崎城西高校、大垣日大高校
(番外編)学年1位または成績優秀者を輩出した高校
天白高校、日進西高校、愛工大名電高校、名古屋大谷高校
※ 成績優秀者・・・成績が学年トップクラスで、なおかつ卒業生代表などに選ばれた生徒
名古屋市天白区の植田で塾を探すなら個別指導のヒーローズ!!
★ 直接のお問い合わせ ★
――――――――――――――――――――――
個別指導ヒーローズ 植田一本松校
〒468-0009
名古屋市天白区元植田1-202 金光ビル2F
TEL:052-893-9759
教室の様子(360度カメラ) http://urx.blue/HCgL