マナビバ

塾長です。

今回は高校生からよく出る質問、というか疑問

虚数　$ i = \sqrt{-1} $　は実在しない数なのか？

について考えてみます。

２次方程式と２次関数のおさらい

解の公式

まず中学３年生が１学期で習う「２次方程式の解の公式」を思い出してみましょう。

２次方程式$ ax^2+bx+c=0 $の解の公式

$$ x = \frac{ -b \pm \sqrt{b^2-4ac} }{ 2a } $$

判別式

高校１年生になると、さらに「判別式」を習います。
１学期の後半または２学期の初めくらいです。

実数$ｘ$について、２次方程式$ ax^2+bx+c=0 $の判別式をDとすると、

• $D < 0$ のとき、解は０個（解なし）
• $D = 0$ のとき、解は１個（重解）
• $D > 0$ のとき、解は２個

続いて、２次関数$ y=ax^2+bx+c $のグラフと判別式Dとの関係について習います。

２次方程式$ ax^2+bx+c=0 $の解を、次の連立方程式の解とします。

$$ \begin{cases}
y=ax^2+bx+c \\
y=0
\end{cases} $$

$x-y$平面上で２式それぞれのグラフを描くと、その交点が解になっているのでした。
つまり、

２次方程式$ ax^2+bx+c=0 $の判別式をDとする。
$ y=ax^2+bx+c $と$x$軸との共有点は、

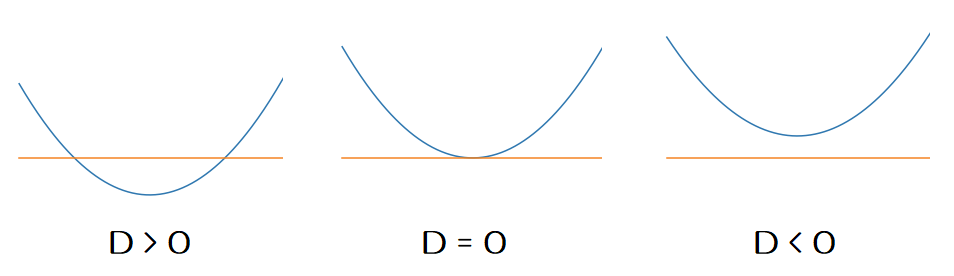
• $D < 0$ のとき、０個
• $D = 0$ のとき、１個（接する）
• $D > 0$ のとき、２個（交わる）

この様子を直感的なグラフで表すと、次のようになります。

複素数

高校２年生では、虚数単位 $ i = \sqrt{-1} $ を導入して、$x$を実数から複素数へ拡張します。
すると方程式の解を必ず求めることができるようになります。

２次方程式$ ax^2+bx+c=0 $の判別式をDとすると、

• $D < 0$ のとき、解は複素数で２個
• $D = 0$ のとき、解は実数で１個（重解）
• $D > 0$ のとき、解は実数で２個

であり、どの場合でも解は、

$$ x = \frac{ -b \pm \sqrt{b^2-4ac} }{ 2a } $$

と表すことができる。
特に$D < 0$ のときは$ i = \sqrt{-1} $ として、

$$ x = \frac{ -b \pm \sqrt{|D|} i }{ 2a } $$

である。

ざっと、ここまでが中３、高１、高２の二次方程式と二次関数のおさらいです。

複素数の世界では必ず共有点がある？

素朴な疑問

さて、ここで塾長は、ふと疑問に思いました・・・

せっかく複素数まで拡張して、判別式$D<0$の場合でも解が求まるようになったのに、対応するグラフの共有点が無いままって、寂しくない？

寂しいですよね！？

疑問です。というか、不満です。
なんとかして、このモヤモヤを解消する必要があります。

問題解決というヤツです。

仮説を立ててみる

そこで、

もしかしたら、グラフを複素数まで拡張すれば、共有点が２つに見えるのではないか？

という仮説を立ててみました。

本当にそうなるのでしょうか？

コンピューターの力を借りて、そのグラフを描くことにチャレンジすることにしました。

仮説を立てて確かめるってヤツです。

４次元のグラフは描けない！！

コンピューターは具体的な数値しか扱うことができません。
そこで今回は、つぎの関数を例に、グラフを描いてみることにします。

$$y=x^2-2x+2 $$

もちろん、これの判別式Dは負です。

$$D=(-2)^2 – 4 \times 1 \times 2 = 4-8 = -4 < 0$$

そして方程式$x^2-2x+2=0$の解は

$$x=1 \pm i$$

という虚数解です。

今回の目的

今回の目的を次のように設定します。

ｘを複素数としたときに、
$$ \begin{cases}
y=x^2-2x+2 \\
y=0
\end{cases} $$
の共有点が２つあることをグラフで示す！

実数と複素数で何がどう変わる？

高校１年生までは、$x$も$y$も実数ですから、これは、

実数$x$ を与えると、実数$y$ が１つに定まる関数のグラフ
つまり、
数直線上の１つの実数$x$を、また別の数直線上の１つの実数$y$へ移し変える関数のグラフ

ということになります。
つまり「２本の数直線」があれば、話ができます。
よって、

$x$ が実数ならば、
$y=x^2-2x+2 $ のグラフは、ｘ軸とｙ軸で構成される「平面（２次元空間）」の上に描くことができる

ということです。
直線は「１次元」ですから、２本の直線で表現できる空間は、せいぜい「２次元空間」となります。

さて、

ここで$x$を複素数に拡張します。
そこで２つの実数$a,b$を使って$x=a+bi$としましょう。

$$ \begin{cases}
y=x^2-2x+2 \\
x=a+bi \\
i = \sqrt{-1}
\end{cases} $$

すると、式の計算結果$y$も複素数になります。
そこで２つの実数$c,d$を使って$y=c+di$としましょう。
すると、これは、

複素数$x=a+bi$ を与えると、複素数$y=c+di$ が１つに定まる関数のグラフ
つまり、
実数平面上の座標$(a,b)$を別の実数平面上の座標$(c,d)$に移し変える関数のグラフ

ということになります。
つまり「２つの平面」があれば、話ができます。
よって、

$x$ が複素数ならば、
$y=x^2-2x+2 $ のグラフは、平面a-bと平面c-dで構成される「４次元空間」の中で描くことができる

ということです。
平面は「２次元」ですから、２つの平面で表現できる空間は、せいぜい「４次元空間」となります。

拡張し過ぎた

上の考察から、コンピューターで「４次元のグラフ」を描けば、今回はミッションクリアできそうです。

・・・ん？

無理です！

私たちはどんなに精神を研ぎ澄ませても、３次元までしか空間の広がりを認識することができません。
ましてやグラフを描くことも見ることもできません。

これはコンピューターでも表示できません。

（計算だけならできます。表示が無理ということです）

グラフを３次元にまとめる！

ということで、何とかして３次元で済ませる方法を考えなければいけません。

グラフを３次元で描けるようにする

という「課題」が生まれてしまいました。

どうしたらよいでしょうか？

【豆知識】
問題解決の世界では、最終的に解決する「目的」のことを「問題」と呼びます。
そして、問題を解決する過程（途中）で乗り越えるべき「目標」のことを「課題」と呼びます。

そもそも何がしたかったのか？

道に迷ったら、目的の再確認です。

目的さえ達成すればよいのです。
もしかしたら「やらなくても良いこと」で悩んでいたりするかもしれません。

今回は、$y=x^2-2x+2 $ と $y=0 $ の共有点が２つあることをグラフで描きたかったのでした。

あ、な～るほど！

次元を減らす

目的の式をじーっと眺めていたら、思いつきました。

$ y=0 $なのですから、$y$の方は２次元も必要ありませんね。

だって０（ゼロ）の時だけ考えればよいのですから。そこで、

ｙの次元を２次元から１次元に減らす！

ことを考えましょう。

グラフ表示の方針

ということで、グラフに表示する方針をまとめましょう。

実数の世界のグラフは、横軸がｘ軸、縦軸がｙ軸です。

今回は$ｘ$を複素数$a+bi$へ拡張したのですから、そのグラフは、

• $ｘ軸$を複素平面$a+bi$へ拡張（平面：２次元）
• $ｙ軸$も複素平面$c+di$へ拡張（平面：２次元）

としたかったのですが、無理でした。
これではグラフの座標が (a,b,c,d) の４次元になってしまい、描けないからです。
そこで次の方針としたのでした。

• $ｘ軸$を複素平面$a+bi$へ拡張（平面：２次元）
• $ｙ軸$は１次元に落とした値（直線：１次元）

つまり、

• 横軸だったｘ軸は、横に広がる複素平面に拡張
• 縦軸だったｙ軸は、実数の数直線のまま

これなら３次元の立体的なグラフで表すことができます。

あとは、縦軸のｙをどのような値に決めるか、ですね！

案１：ｙの実数だけを縦軸にとる　→　失敗！

そもそもグラフは実数しか描けません。
そのため、１つの複素数を２つの実数の組に対応させ、それを平面上に表すのでした。

であるならば、安直ではありますが、ｙの実部だけをグラフに採用すればよいかもしれません。

• 横軸：複素数$ x=a+bi $（平面：２次元）
• 縦軸：$ｙ=c+di $の実部$c$（直線：１次元）

それでは、この案でグラフを描いてみましょう。
こうなりました。

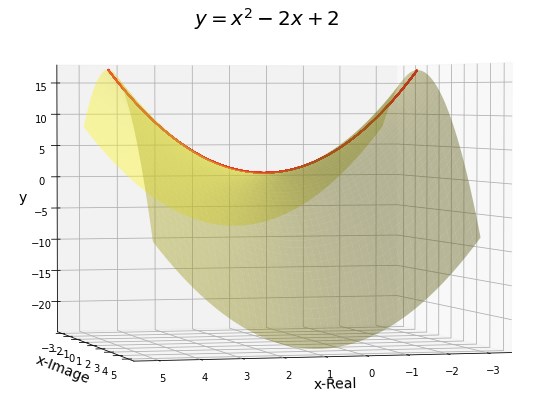
馬の鞍みたいな形のグラフになりました。
最後の考察で、このグラフも少し使いますから、とりあえず「馬の鞍型」のグラフとでも呼んでおきましょう。

ちなみに、赤い線が、実数の$x-y$平面上のグラフ（平面 $ b=0 $ で切った切り口）です。

さて、これで目的は果たせたでしょうか・・・？

うーん、何だかよく分かりません。

$x$を複素数に拡張したおかげで、確かに平面$y=0$との共有点は存在しそうです。
しかし「共有点が２つ」である様子が、これでは分かりません。

よく考えてみたら、これはダメです。

もしも４次元のグラフが描けるとすれば、本来のグラフは、

(a,b,c,d) の４次元でグラフを描き、それを平面$c=0$でカットした切り口が、求める３次元のグラフ

が本当のグラフです（※）。
４次元のグラフは描けませんが、本来はそんな感じです。

そう考えると、無条件に$y$の虚部を捨ててしまったのがダメでした。

（※）【豆知識】
４次元の立体を平面で切ると、その切り口が３次元の立体になります。
私たちの世界は３次元です。私たちの世界で立体は３次元です。
例えば、スイカを包丁で切った時の断面を想像してみてください。
スイカは３次元の球です。それを２次元の平面でスパッと切ると、切り口が２次元の円になります。
４次元の世界は、私たちの世界よりも１つ次元が上ですから、上の考察をすべて１つずつランクアップして考えます。
つまり、４次元の中で球体を切ると、切り口が３次元の球になります。

案２：ｙの絶対値を縦軸にとる　→　成功！

そこで、数学的に条件を壊さないことを考えます。

$y=c+di=0$

すなわち、

$c=0$かつ$d=0$の場合

を考えたグラフであれば目的を達成できるわけです。

ところで、

$|y|=0$も同様に$c=0$かつ$d=0$です。

ですから縦軸を$|y|$とすれば、これは実数ですから、うまく１次元に収まります。

• 横軸：複素数$ x=a+bi $（平面：２次元）
• 縦軸：$|ｙ|$すなわち$\sqrt{c^2+d^2} $（直線：１次元）

それでは、この案でグラフを描いてみましょう。
こうなりました。

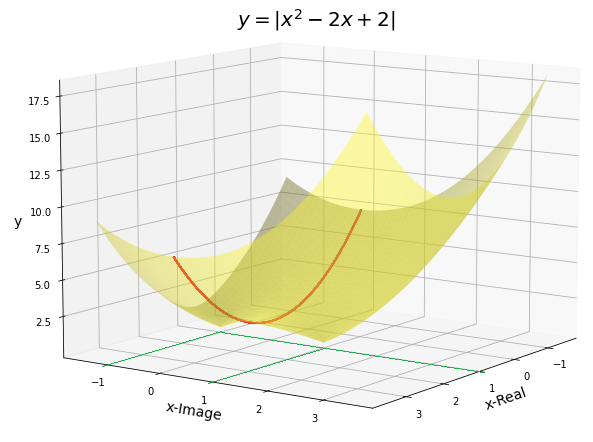
うまくいきました！

グラフの２カ所が尖っていて、２つの虚数解

$$x=1 \pm i$$

の所で平面$y=0$に突き刺さっていそうです。
共有点は「２だけ」ですから、平面$y=0$上で、それぞれ１点ずつ、チョン、チョンと、くっ付いているはずです。

グラフの解像度の問題で「点」まで鋭利に描き切れていません。
念のため、１００倍に拡大してみましょう。

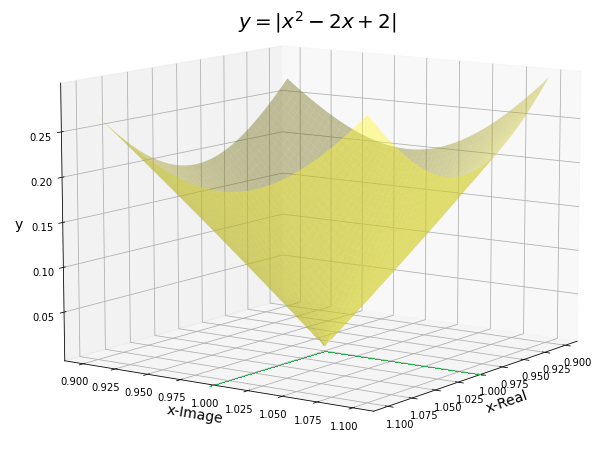
$x=1 + i$の付近を１００倍に拡大してあります。
この倍率で$x=1 – i$も同時に描くのは不可能なので、１つだけで確認します。

どうです？

共有点の１つ$x=1 + i$の位置へ、グラフが突き刺さっている感じがしますよね。
このグラフを１０００倍にしても、１００００倍にしても、ずっとこんなグラフになります。

「１点に突き刺さ差っている！」

のですから、倍率をどこまで上げても、こんな感じです。
もちろん、$x=1 – i$ についても同様です。

これで本当に

「たった２点」だけの共有点を持つ！

ことが、グラフで表示できたのではないかと思います。

思ったより大変でした。

教えてエライ人！

上のような考察をFacebookにアップしていたら、色々な人からご意見をいただきました。
なかでも吉田先生には色々と教えていただきました。

ということで、今回のエライ人は、吉田信夫先生です！

吉田先生はあの「大学への数学」で原稿を書かれていた先生の内の１人です。
超すごくないっすか！

先生のブログ「yoshidanobuo’s diaryー高校数学の“思考・判断・表現力”を磨こう！」はこちらです。

グラフで虚数解を見える化するにあたり、いろいろとご指導をいただきました。
また数学的におかしな用語の使い方についてもご指摘いただき、修正することができました。

用語の誤用

今回やってしまった用語の誤用を２つ紹介します。

どこが間違っているのか、考えてみてください。

• 誤用１：「$y=x^2-2x+2$の判別式の値は負です。」
• 誤用２：「複素数$x=a+bi$と実数$y$において、$y=|x^2-2x+2|$のグラフ(a,b,y)は、平面$y=0$と２点で接しています。」

わかりますか？

私は吉田先生に指摘されるまで気づかなかったです。まさに

「それは違反です」

という感じで、御用とあいなりました。

大学入試の２次試験で記述回答を予定している人は、気を付けてくださいね。

さて、上のものは次の点で間違っていました。

• 誤用１：関数に対して判別式を語ったところがアウト。判別式は方程式「$0=x^2-2x+2$」に対して定義されるもの。
• 誤用２：「接する」は「微分可能な領域」で定義されるもの。今回は尖っていて微分不可（微分する向きによって微分係数が異なる）。

さぁ、どうでしたか？

滑らかに「接する」グラフにする

さらに誤用２に関連して、グラフが２つの$x=1 \pm i$で「接する」ようなｙの取り方も教えていただきました。

みなさん、分かります？

• 横軸：複素数$ x=a+bi $（平面：２次元）
• 縦軸：$|ｙ|^2$すなわち$ c^2+d^2 $（直線：１次元）

それでは、この案でグラフを描いてみましょう。
こうなりました。

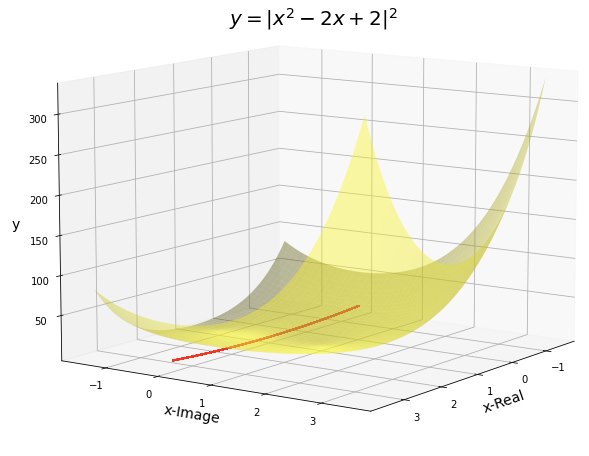
ｙの値が２乗されているので、グラフが大きくなりすぎて「２点」どころではなくなってしまいました。
そこで例によって、$x=1 + i$の付近を１００倍に拡大してみましょう。

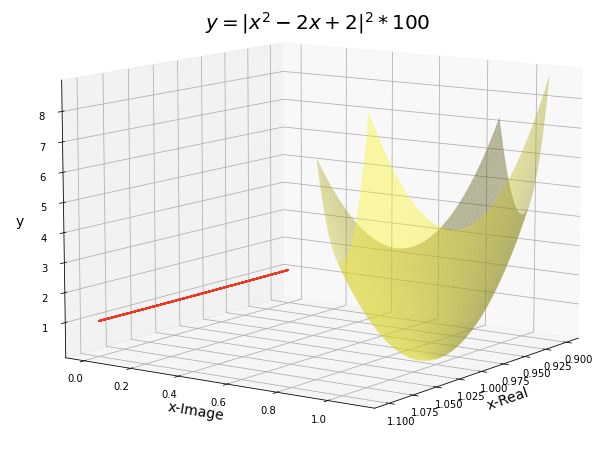
おお、本当に滑らかに接してそうですね！

例によって「１点」で接しているので、このグラフを１０００倍にしても、１００００倍にしても、ずっとこんなグラフになります。

次元を減らすもう１つの方法

さらにさらに、吉田先生からもう１つのグラフ表示の方法を教えていただきました。
$x=a+bi$ としたときに$y=0$を満たすような

$y=0$　を　(a,b)　だけで描く！

です。

つまり、(a,b)に色々な実数を当てはめて　$x=a+bi$　を動かしたときに、$y$　がどのように動くかを図示します。
もう少し正確に言うと、$y=0$　を満たすような「ｙの実部」と「ｙの虚部」をそれぞれ平面(a,b)上に図示します。

$y$　の値もまた　(a,b)　の関係式として表現されるため、グラフの次元は(a,b)の２次元だけで済みます。
１つの複素平面だけで示すやり方です。

やってみましょう。まず、

$$ \begin{cases}
y=x^2-2x+2 \\
x=a+bi \\
y=c+di
\end{cases} $$

について、

$x=a+bi$　を　$y=x^2-2x+2$　に代入して整理すれば、

$$ y=a^2-b^2-2a+2+2b(a-1)i $$

です。

$y=c+di=0$　すなわち　$c=0$かつ$d=0$　の場合を考えるわけですから、

$$ \begin{cases}
a^2-b^2-2a+2=0 \\
かつ\\
2b(a-1)=0
\end{cases} $$

すなわち、

$$ \begin{cases}
b = \pm \sqrt{(a-1)^2+1} \\
かつ \\
a=1　または　b=0
\end{cases} $$

です。
これらの交点が求める解になります。

あらためて、実部の$a$を$x$とし、虚部の$b$を$y$として、複素平面$x-y$にグラフを図示したのが下です。
これは吉田先生からいただいたグラフです（軸が$x-y$になっていますが、$a-b$に読み替えてください）。

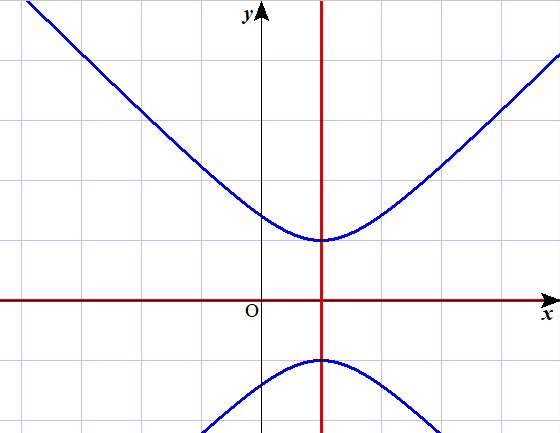
$a^2-b^2-2a+2=0$のグラフが青で、$a=1$と$b=0$のグラフが赤です。

確かに複素平面の世界では、２点の共有点がありました。
そしてグラフの交点はそれぞれ、$ 1+i $　と　$ 1-i $　です。

これは感動です！

考察とまとめ

もしも

$$ \begin{cases}
y=x^2-2x+2 \\
x=a+bi \\
y=c+di=0
\end{cases} $$

のグラフを４次元　$(a,b,c,d)$　の空間上に描けたとしましょう。

すると、上の吉田先生からいただいた平面グラフは、その４次元グラフを　$y=0$　で切った切り口であるといえます。

やってみました。それが下のグラフです。

緑の実線が、実数の世界での２次関数のグラフです。
赤の実線と青の実線は、それぞれ上の平面グラフに対応しています。

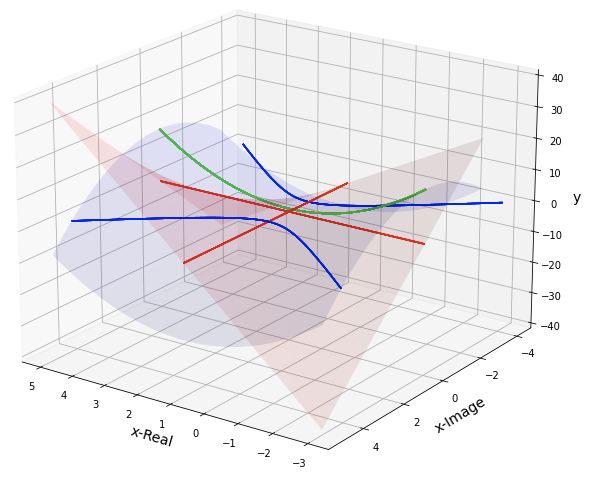
このグラフをもとに、これまでの話を全て振り返ってみます。

まず青い曲面が、最初に描いた「馬の鞍型」のグラフです。
これは４次元グラフを平面 $ d=0 $ で切ったときにできる立体です。
そして、この青い曲面をさらにｙ＝０で切ると、青い実線の双曲線になります。

次に、４次元グラフを平面 $ c=0 $ で切ったときにできる立体も考えます。
それが、上のグラフの赤い曲面です。
そして、その赤い曲面をさらにｙ＝０で切ると、赤い実線の２直線になります。

そして青い双曲線と赤い直線の交点が、まさに　$ 1 \pm i $　となっています。

これらの様子を総合すると、２次方程式の虚数解　$ 1 \pm i $　は、

• ３次元空間　(a, b, c)　の曲面（縦軸をｙの実部としたグラフ）
• ３次元空間　(a, b, d)　の曲面（縦軸をｙの虚部としたグラフ）
• ｙ＝０の水平な平面

の３つを重ねた時にできる共有点

であることがグラフで確認できました。

グラフ表示に使ったPythonプログラム

今回、グラフを描くのにプログラミング言語の「パイソン（Python）」を使いました。
以下が、そのプログラムです。
Jupyterという環境を使いました。

ちなみに、パイソンのプログラミングを学ぶなら、無料で使える Google Colaboratory がオススメです。
もちろん下のプログラムも Google Colaboratory で動作します（動作確認済）。

import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
%matplotlib inline
fig = plt.figure(figsize = (8, 8))

# Axes3D
ax = Axes3D(fig)

# タイトルを設定
ax.set_title(“$y=|x^2-2x+2|$”, size = 20)
#ax.set_title(“$ y = |x^2-2x+2|^2 *100 $”, size = 20)

# 軸ラベルを設定
ax.set_xlabel(“x-Real”, size = 14)
ax.set_ylabel(“x-Image”, size = 14)
ax.set_zlabel(“y”, size = 14)

# 表示角度の設定
ax.view_init(elev=10, azim=35)

# 座標のメッシュ
rr = np.linspace(-1.5, 3.5, 200)
ii = np.linspace(-1.5, 3.5, 200)
#rr = np.linspace(0.9, 1.1, 200)
#ii = np.linspace(0.9, 1.1, 200)
i0 = np.zeros(200)
r,i = np.meshgrid(rr, ii)
z = r + i*1j

# 曲線・曲面を描画
y0 = r*r-2*r+2
ax.plot_wireframe(rr, i0, y0, color = “red”)
y = np.abs( z*z-2*z+2 )
#y = ( np.abs( z*z-2*z+2 ) )**2 *100
ax.plot_surface(r, i, y, color = “yellow”, alpha=0.4)
plt.show()

あとがき

どの学年も文字式と関数の季節になりました。

今年から中学生は教科書改訂で「主体的な学び」が重視され、プログラミング教育も強化されました。
来年からは高校生でもそうなります。

そういう流れの中で、今回は、

高校生のレベルで数学を題材に「主体的な学び」を「プログラミング」も活用して行ったらどうなるか？

を実践してみました。

さらに今後の常識というか、新しい価値観である

「集合知」で「問題解決を加速する」という姿勢

も取り入れてみました。
ですから、問題解決の用語や流れも、それとなく意識してあります。

これが次世代型の教育であり、同時に、いま日本で遅れてしまっている教育でもあります。

今のところ私はそのように思っております。

教育者も間違えます。
先生が何でも知っていて間違いを起こさない聖人君子である、なんていう時代は終わっています。
そもそも非科学的で不合理です。

もう、１人の聖人君子や、優れたリーダー、１部の天才に問題の解決を任せるよな時代では、ありません。
というか、そんな人はいません。
幻想です。

今や、世界中の人たちがコンピューターでつながっているのです。
みんなが意見や知恵を出し合う「集合知」で、いち早く問題を解決していこう！
そのように考える方が大切です。

このような価値観でコンピューターを活用しながら問題解決を実践できる人。

それが、これから日本で、いや世界で多く必要とされる人たちなのだと思います。

現場からは以上です。

生徒・保護者様のお友達登録はこちら

LINE登録するとプレゼントがもらえます！
【会員限定】お子様の成績と可能性を伸ばす１８個のノウハウ

塾関係者様のお友達登録はこちら

LINE登録するとプレゼントがもらえます！
「zoomで簡単。オンライン授業移行の教科書」
または個別対談も可

名古屋市天白区の植田で塾を探すなら個別指導のヒーローズ！！

★ 直接のお問い合わせ ★
――――――――――――――――――――――
個別指導ヒーローズ　植田一本松校
〒４６８－０００９
名古屋市天白区元植田１－２０２　金光ビル２Ｆ
ＴＥＬ：０５２－８９３－９７５９
教室の様子（360度カメラ）　http://urx.blue/HCgL