塾長です。
テスト期間に突入しました。
みなさん、テスト対策は万全ですか?
学校からのプリントや宿題も増える頃ですよね?
そんな中、とある中3生。
「なかなか解けない!」
と悩んでいました。
「遺伝の規則性」・・・学校から出された理科の課題だそうです。
遺伝の組み合わせの全パターンを、もれなく書き出して数える・・・見るからに大変そう。
さて、皆さんは、こんな時どうしますか?
Contents
めんどうな事はコンピューターにやらせる!
ということで、本日のタイトルが答えです。
そう、コンピューターの出番です。
サックっとプログラミングした方が早いです。
プログラミングは多少の練習が必要です。
しかし慣れてしまうと、色々な作業が楽になります。
最初の1回目の作業は、規則性を理解するため、自分が成長するために必要です。
しかし、2回も3回も同じ苦労をするのが良いとは限りません。
2回目、3回目について、
全く同じ苦労をしますか?
何か工夫をして効率を上げますか?
こういうときの瞬間、瞬間の工夫の積み重ねで、人生が大きく変わっていくように思います。
その工夫のためには、プログラミングは必須アイテムと言えましょう。
それでは、コンピューターにやってもらいましょう。
遺伝の規則性についての例題
その前に、まず今回の問題について説明します。
中3理科の遺伝です。エンドウ豆の種子が「丸い」のか「しわ」なのか、という問題。
毎年の恒例です。
「丸い」種子をつける純系のエンドウ豆があります。
「しわ」の種子をつける純系のエンドウ豆があります。
それぞれから1株ずつ対応させて交配させると、子の世代の種子はどのような形状になるでしょう?
丸い種子のエンドウ豆の株と、しわの種子のエンドウ豆の株の数を、簡単な整数比で示せ。
また「丸い」形質の遺伝子をAとし、「しわ」の形質の遺伝子を「a」として、そうなる理由を説明せよ。
このように遺伝の問題は、組み合わせの全パターンで考えて解くのでした。
中3数学で習う多項式の分配法則 (A+A)(a+a) = Aa+Aa+Aa+Aa に似ています。
そして回答の例はこんな感じです。
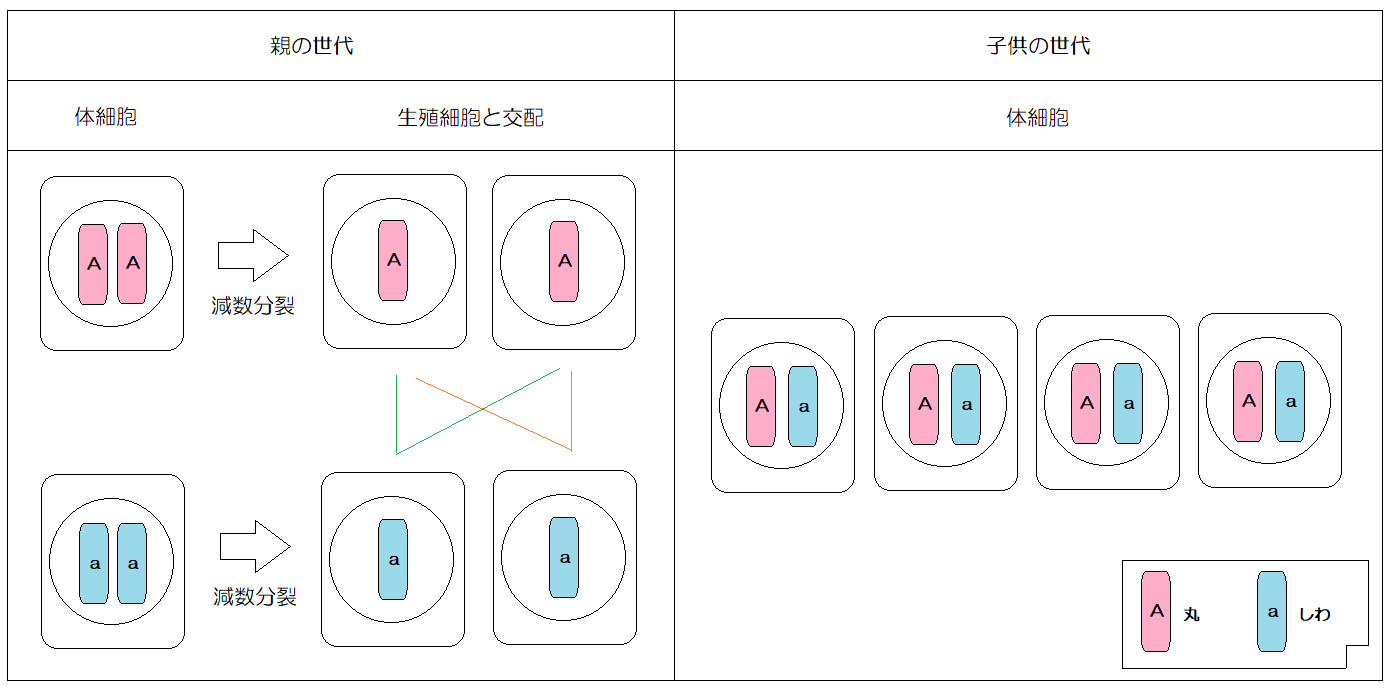
純系の「丸い」種子をつける親の体細胞の遺伝子を(A, A)、「しわ」のそれを( a, a )とする。
子の世代は(A, A)と( a, a )の掛け合わせが(A, a )(A, a )(A, a )(A, a )となる。ここでAは「顕性の形質」で、a は「潜性の形質」だから(A, a )は「丸い」種子となる(※)。よって、子の世代の種子は、全て「丸い」形状になる。
孫の世代は、子の(A, a )と(A, a )の掛け合わせが(A, A)(A, a )(A, a )( a, a )となるから、「丸い」:「しわ」が3:1の比率であらわれる。
(※)教科書改訂により古い用語の「優性」「劣性」は廃止され、「顕性」「潜性」に統一されました。
詳細は教科書を見てくださいませ。
やっとれん
これが「ひ孫の世代」以降になると厄介です。組み合わせが指数関数的に増えてしまい、調べるのが煩雑になります。
例えば、こんな問題です。
純系の「丸い」種子の株と「しわ」の種子の株を掛け合わせて子の世代をつくる。
その子の世代どうしを掛け合わせて、孫の世代をつくる。
その上で、次の各問いに答えなさい。(問1)孫の世代を互いに掛け合わせたとき、次の世代の「丸い」:「しわ」の比はどうなるか?
(問2)孫の世代の中から「丸い」種子の株だけを選んで、互いに掛け合わせたとき、次の世代の「丸い」:「しわ」の比はどうなるか?
こんな問題が出たら、やってられません。
他の問題をやる時間が無くなってしまいます。飛ばしてください。
出るのが明白なら、事前に答えを丸暗記して流しましょう(出ないと思いますが)。
コンピューターにやってもらいました
しかしコンピューターなら、あっという間です。
親の世代から、上の問1と問2にある「ひ孫の世代」まで、コンピューターに聞きました。
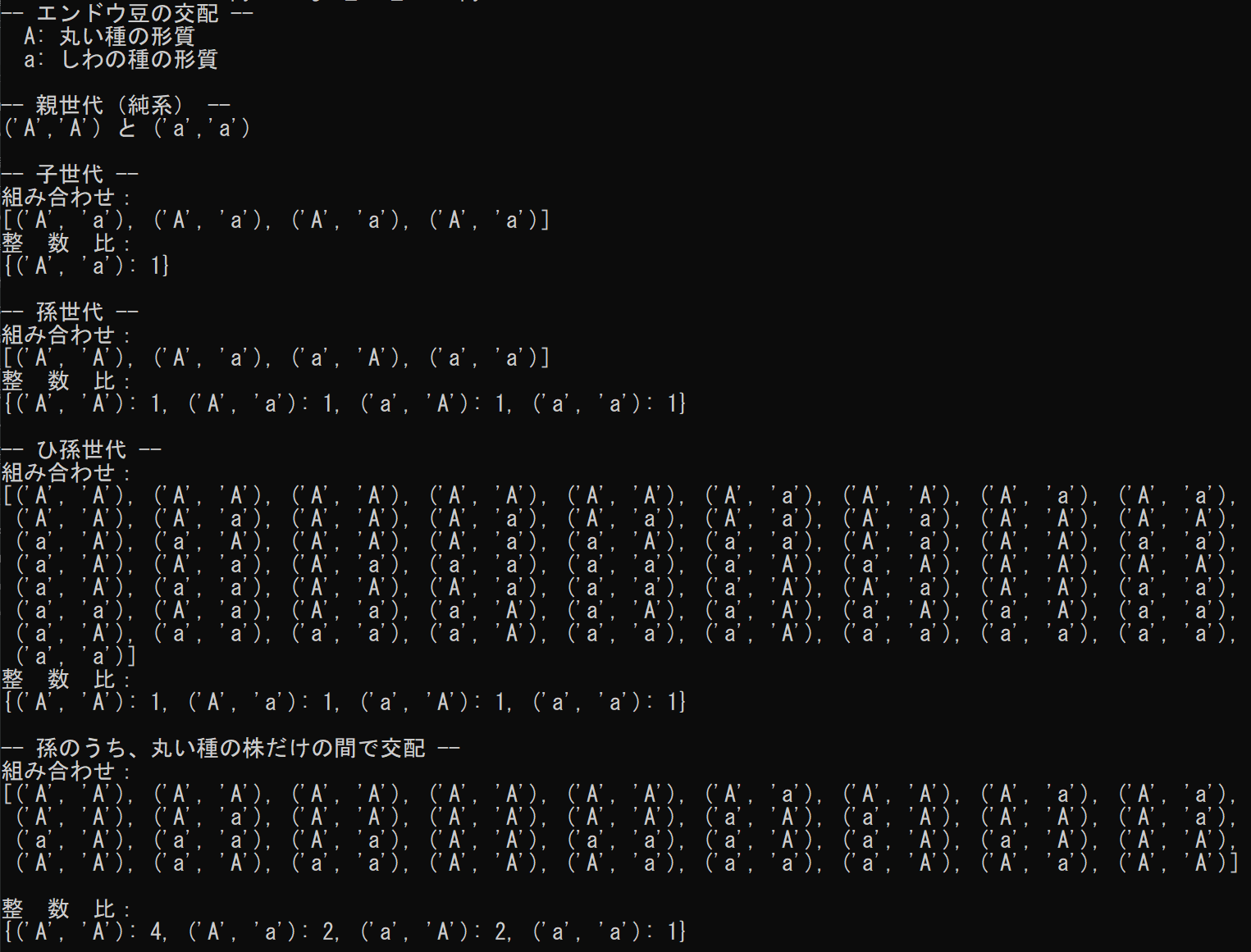
エンドウ豆の遺伝についてパイソンのプログラムで組み合わせを計算させた結果
問1の方は、孫の世代も、ひ孫の世代も、「丸い」種子の株と「しわ」の種子の株の比率は同じでした。
ガチで数えると64通りの組み合わせですが、同じものをまとめていくと3:1になりました。
つまり何も操作をしなければ、エンドウ豆は「丸い」:「しわ」=3:1の出現比率に落ち着くと言えます。
問2の方は「丸い」種子だけを選択する操作をした場合です。当然ですが、次の世代で「しわ」の割合が減ります。
なんと8:1になりました。
何世代目で純系になる?
ちなみに、さらに「丸い」株だけを選択して次の世代「玄孫(やしゃご)」を生むと、15:1になります。
さらに「丸い」株だけを選択して次の世代・・・と繰り返していくと、いつかは「丸い」種子の株だけになるというワケです。
こうして純系の株が作られていくワケですね。すると
何世代の後に「丸い」の純系を得られるか?
が気にってきます。確率ですから「しわ」を完全に0にすることは難しいので、ここでは仮に「純系」の基準を
「しわ」の出る確率が1万分の1以下
としましょう。
そこで、この基準を満たすまで世代交代を繰り返す実験をやってみました。
もちろん、コンピューターの中で・・・。
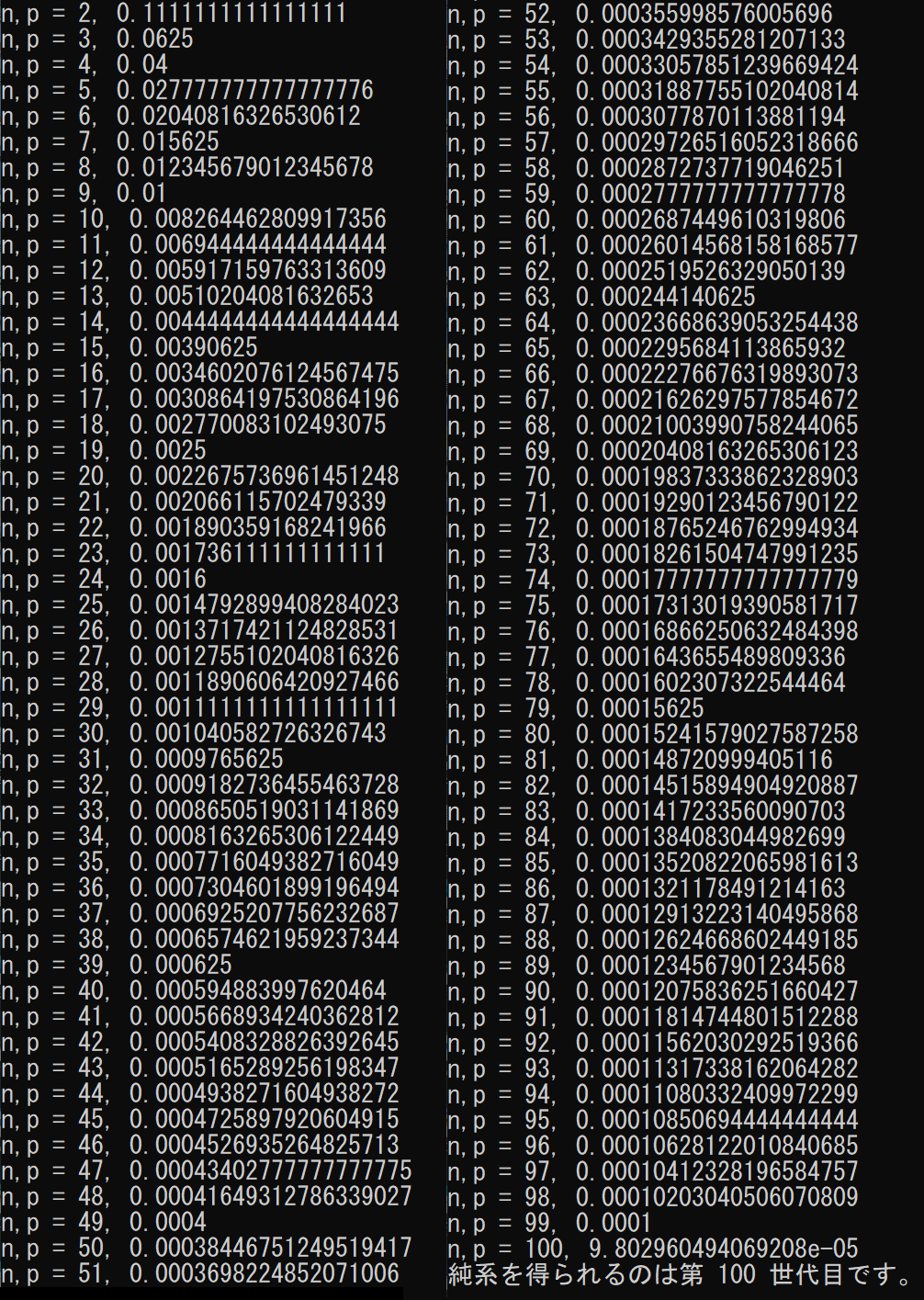
ということで、第100世代目で「ほぼ純系」の子孫ができました。
狙ったワケではありませんが、ちょうど100でした。
シミュレーションですから、交配の全パターンを計算しています。
結果が出るのに4時間くらいかかりました。
メモリは20ギガくらい使いましたが、塾長のパソコンは16ギガしか積んでいなかったのでメモリ不足になり、途中から計算が遅くなりました。
確率漸化式をつくって計算すれば、もっと早く回数を求められるとは思いますが、それでは高校数学の話になってしまいます。
今回は、あくまでも「中3理科の遺伝の実験」としてプログラミングしました。
ただ今回は(A, a )と(a, A )を別のものとして処理しました。
これらを一緒と見なすプログラムを追加すれば、組み合わせの数を何割か減らせたので、もう少し高速にシミュレーションできたかもしれません。
何はともあれ、やってみた感想は・・・
そもそも、純系の株を作るのが、ものすごく大変だ!
ということでした。
シミュレーションではなく、これが本当にエンドウ豆を交配していくことを考えてみてください。
成長を待って、種を採取し、分類し、また植えて、花が咲く前におしべを切り・・・ということを延々と続けていくわけです。
1000株育てて100株に選定などとすれば、もっと早く純系を得られるとは思いますが、それでも大変でしょう。
実験は準備が9割と言われますが、むしろ99%くらいに感じます。
これが今日の結論と言っても良いでしょう。
作業が大変なのか、理科として難しいのか?
組み合わせのパターンを全て考える。
組み合わせの組み合わせを全て考える。
組み合わせの組み合わせの、そのまた組み合わせを全て考える。
どんどん煩雑になって、数え上げるのに苦労します
解けない理由が、理科として難しいからではありません。
「作業がたいへん!」
という意味で難しい。
リアル世界の実験では、乗り越えなければいけない困難でしょう。
しかし学校の勉強やテストとなれば話は別です。
例えば、制限時間の厳しいテストや入試が、このような作業量を手早くこなせるか否かで合否が決まるものであったら、ちょっと意味不明です。
教科を分ける意味がほとんどありません。
機械が無かった時代は「機械みたいな人間」が重宝されたかもしれませんが、今はスマホでさえ高速に処理できます。
大変と思う時こそ、コンピューターの使い方お教えるべきなんです。
時には根性論も大切ですが、それだけは良くありません。
もっと積極的にコンピューターを活用すべきだと思います。
あらゆる勉強にコンピューターを活用!
遺伝の組み合わせを計算させるプログラムをつくる過程で、遺伝の性質を深く理解できるでしょう。
手作業で組み合わせを書き出すのも無駄ではありませんが、それが大変過ぎる作業では、先に心が折れてしまいます。
それに作業の制約が勉強の制約になってしまうと、むしろ視野が狭くなります。
コンピューターの計算は、失敗してもやり直しが楽です。
何度もチャレンジできるし、視野も広がるでしょう。
また多様なメディアを扱えるというメリットもあります。
子供たち自身でコンテンツを作ることもできます。
数学や理科、技術だけで活用というのでは寂しいです。
美術、音楽、体育、社会、英語・・・あらゆる科目で使いこなすことができます。
今回は理科の勉強にコンピューターを活用する例を考えました。
コンピューターを活用するセンス
これを子供たちに身に着けてもらうことが大切です。
そのためには、あらゆる学びの場でコンピューターを活用しましょう。
たとえば今回のように、「ワーク」にあたる作業訓練的な学びの部分には、コンピューターを活用できるところが多くあるはずです。
速く、正確に、たくさん・・・
このような意味で能力を伸ばすような訓練系の学習時間は、今後、見直されていくべきでしょう。
今後は、コンピューターを活用した試行錯誤の時間に置き換わっていくべきだと思います。
このような視点に立つと、日本の教育は世界から遅れています。
創造性やイノベーション力が足りないと、今でも言われています。
少ない知識をトリッキーに組み合わせて「速く、正確に、たくさん」できるような訓練ばかりして、消耗しているからです。
そういう作業こそ、コンピューターにやらせるのです。
それが当たり前の時代です。
やらなければ、日本が沈没します。
パイソンでプログラミング
今回のプログラムは次の通りです。
パイソンのバージョンは3.9以降です。
最大公約数を求める関数 math.gcd() に3つ以上の引数を渡せるのが、そのバージョン以降だからです。
データ構造としては、タプル、配列、辞書を理解しておく必要があります。
パイソンはタプルを辞書のキーとして使えることを利用しています。
また、パイソンは配列やタプルに自然数をかけると、それらを複製できることも利用しています。
(A, A)×3 → [(A, A),(A, A),(A, A)]
これらの機能は他のプログラミング言語でも使えるとは限らないので要注意です。
なお、純系を何世代目で得られるかを求めるプログラムの部分は省略してあります。
興味のある人は考えてみてください。

現場からは以上です!
生徒・保護者様のお友達登録はこちら
LINE登録するとプレゼントがもらえます!
【会員限定】お子様の成績と可能性を伸ばす18個のノウハウ
塾関係者様のお友達登録はこちら
LINE登録するとプレゼントがもらえます!
「zoomで簡単。オンライン授業移行の教科書」
または個別対談も可
名古屋市天白区の植田で塾を探すなら個別指導のヒーローズ!!
★ 直接のお問い合わせ ★
――――――――――――――――――――――
個別指導ヒーローズ 植田一本松校
〒468-0009
名古屋市天白区元植田1-202 金光ビル2F
TEL:052-893-9759
教室の様子(360度カメラ) http://urx.blue/HCgL




