塾長です。
これからプログラミングを始めたい人からの質問です。
何から勉強したら良いですか?
こういう質問が増えてきました。
塾長は立場上、中高生やアルバイトの大学生から、こういう質問を受けます。
中には他の塾の先生から「子供にプログラミングを教えた方が良いですか?」というご相談も。
ということで、塾長の立場からアドバイスを書きたいと思います。
この記事の対象
この記事では、特定の産業技術を学ぶことを目的にはしていません。
広く通用する「基礎学力としてのプログラミング」を学びたい人が対象となるでしょう。
逆に「数か月~半年後に仕事ですぐ使えるプログラミング」を学びたい人は、別の記事を探してください。
あくまでも学習塾の先生として書きますね。
プログラミング言語の種類が多すぎる
プログラミングを学ぶ上で、最初に立ちはだかる壁。
それは「どのプログラミング言語を選ぶか?」かもしれません。
せっかく学ぶなら、色々なことができそうな言語を選びたいものです。
しかし、プログラミング言語の種類が多すぎます。
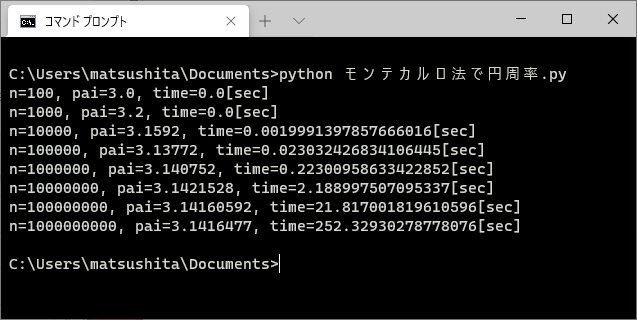
例えば、下の図を見てください。
塾長の独断と偏見でいくつか名前を挙げて描いたのですが、それだけでも、この数です。
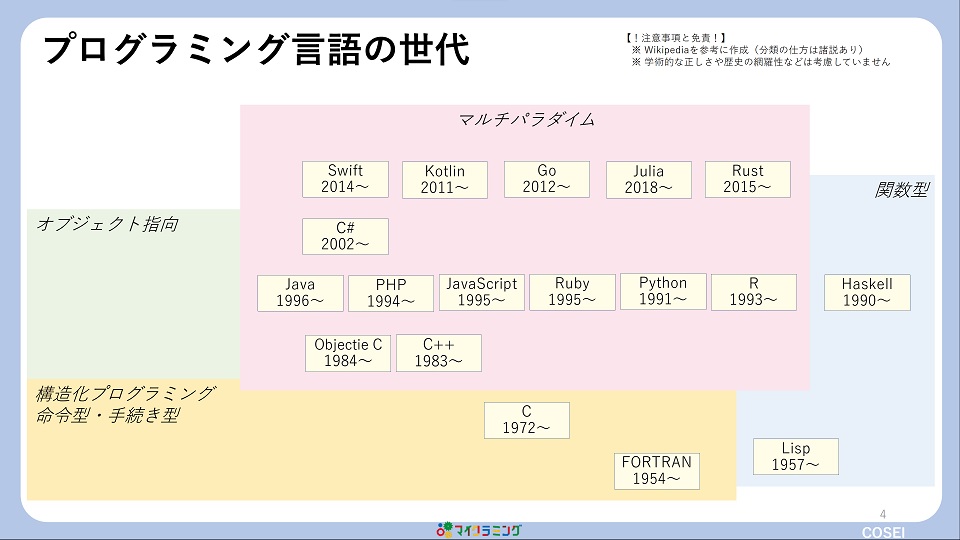
もちろん、この図でもまだまだ描き足りません。
「PHPの前にPerl がない」とか「歴史を語るなら Pascal も必須」とか「我が青春の BASIC が無いとは何事だ!」など文句を言われそうです。
要するに、それくらい多くのプログラミング言語があるということです。
それゆえ、選択に迷ってしまうのも無理はないでしょう。
いったい何を選ぶべきやら・・・。
オススメのプログラミング言語は?
そこで塾長は、こんなアドバイスをしています。
全くの初心者であれば、
① スクラッチ
② パイソン
の順に学ぼう!
具体的には、
- 小学生なら、スクラッチ(Scratch)を学ぼう
- 中学生なら、スクラッチ(Scratch)、パイソン(Python)の順に学ぼう
- 高校生なら、パイソン(Python)を学ぼう
- 迷ったら、パイソン(Python)を学ぼう(※)
・・・スクラッチとパイソンだけやないか!
と突っ込まれそうですが、はい、その通りです。
それには、ちゃんと理由があります。
※ ちなみに就職であれば、希望の職種に合ったプログラミング言語を学びましょう
例えば工業系であればC言語やC++、ゲーム業界であればC++やC#、Java、BluePrintなどです。
最初はニュートラルなプログラミング言語で学ぼう!
プログラミング言語をマスターした先人たちは、口をそろえてこう言います。
1つの言語をマスターすれば、他もだいたい一緒だよ👍
しかし初学者にとって、いきなり悟りの境地を語られても参考になりません。
いや、そういうことは聞いてないから😞
と言われそうです。
初学者がプログラミング言語を選択するときの注意点みたいなものはないのでしょうか?
塾長としては、次のことを注意していただきたいです。
初めて学ぶなら、次の5つの観点でプログラミング言語を選びましょう。
- 無料で環境を作れること
- すぐに動かせること
- ネットで検索すれば、すぐに事例や情報を得られること
- マルチパラダイム言語であること(※)
- 多くの分野で使われていること
細かい説明は省きますが、これらの条件を無難にクリアしているのがパイソン(Python)です。
そして、その1歩手前の段階で、直感的にすぐ学べるのがスクラッチ(Scratch)です。
ちなみにスクラッチでも上の1~3までを満たします。
これら5つの観点で選べば、次のようなプログラミング言語に出会えるでしょう。
- 特定の産業分野に偏らない技術を学べる
- 近代的なプログラミングを学べる
要するに技術的にも時代的にもニュートラルで無難と言うことです。
もちろん、無料で学びやすいことも大切です。
※ マルチパラダイム言語とは、色々なパラダイムでプログラミングができる言語という意味です。
※ パラダイムとは、プログラミングの手法やスタイルのことです。手続き型プログラミング、構造化プログラミング、オブジェクト指向プログラミング、関数型プログラミング、ベクトル型プログラミングなど、色々なパラダイムがあります。
ゼロから学ぶ人にありがちな悩みは?
ここから先は「あるあるネタ」みたいなお話です。
初心者がプログラミングを学ぶときに直面しがちな状況について、少しご紹介しましょう。
共感や同情、失笑など、各々楽しんでいただければと思います。
①お手本のプログラムを見て「だから何?」って思う
たいていのプログラミング言語の本は、次のような章構成になっています。
- 環境の構築(インストールなど)
- 画面に Hello World! という文字列を表示させる
- 変数の種類
- 条件分岐と繰り返し
- 関数
・・・
そして50ページほど進めたあたりで思うのです。
- 画面に「Hello World!」って表示させたからって、だから何なの?
- なんか想像してたのと違った。
勉強が先に進んでいる気がしません。
最初は簡単なプログラムから学びますので、大した処理はできません。
そのため最初のうちは
「こんな処理、何の意味があるの?」
と言いたくなるようなプログラムばかり書かされます。
いわゆる「修行」という期間です。
勉強に慣れている人は、修行を乗り越える術を持っているでしょう。
しかし、多くの人にとっては、
「それが将来、どんなことにつながるのか?」
を説明してくれる人が近くにいた方が、希望をもって学べるかもしれません。
②いつま経っても基本ばかり
コンピューターで色々なことができる!
と期待して勉強を始めたのに、いつまで経っても何もできません。
- 数学のグラフを表示させるにはどうしたら良いの?
- ゲームを作るにはどうしたらよいの?
- 人工知能を作るにはどうしたら良いの?
そういうフラストレーションが溜まります。
部活に例えるなら、せっかくテニス部に入ったのに、ラケットを握らず、マラソンばかりやらされる・・・そんな感じでしょうか。
かといって、ページを飛ばして後半の応用へスキップしてしまえば、今度は分からない言葉だらけ。
最初から読み進めていかないと、用語の意味が分からないでしょう。
ちょっとしたプログラムをつくるにも、環境やら文法やら用語やらと、乗り越えるべき「修行」が多いのです。
いきなりC++言語やJavaなどに手を出してしまえば、さらにオブジェクト指向やモジュールの概念なども早い段階から学ぶ必要が出て来ます。
独学ならば、ここで半分の人は心が折れてしまい、挫折してしまうでしょう。
パイソンは修業が少ない!
そんな中で、パイソンは「修行」が少ない言語です。
ゼロとはいきませんが、学ぶにつれて、できることが加速的に広がり、努力が報われやすいでしょう。
また、ネットで検索したり、ChatGPTに問い合わせたりすれば、すぐに答えが見つかるでしょう。
何より、無料でできることの幅がとても広く多いです。
スクラッチでプログラミングの基礎を学んでいれば、さらに楽になります。
パイソンに移行しても、最初の修行の過程を加速し、短縮できるでしょう。
③マウントを取られる
どの世界もそうですが、自分の価値観を押し付けてくる人がいます。
例えば「スクラッチを学んでいる」と話せば、それは簡単すぎるだの、プログラミングとは言えないだの、上から目線で何か言ってくる人が出てきます。
例えば「パイソンを学んでいる」と言えば、最初はC言語をやるべきだとか、オブジェクト指向を知るべきだとか、パイソンは遅いだとか、言われるかもしれません。
マウントを取る人たちが、さも自信ありげに語ってくるので、聞いていると委縮してしまいますね。
でも安心してください。
結論から言えば、あまり気にしなくて良いです。
難しいことを理解している人がエライなんてことはありません。
パイソンで100秒かかる処理がC言語なら0.1秒で済む、ということが事実だとしても、学ぶ時間が1日でも延長してしまったら意味がありません。
「そういう見方もあるんだな。勉強になるな。」
くらいに受け取っておきましょう。
逆にパイソンを学んでいることでマウントを取る人もいます。
流行の生成系AIをはじめ、人工知能の多くでパイソンが使われているためでしょう。
パイソンをやっていると流行に乗っている気がするのかもしれません。
もちろん、あまり気にしなくて良いです。
④何でそうなるのか想像できない
プログラミングは理系のイメージが強いですが、まったく理系っぽくないと思います。
とくに中学生以上では、数学の文字式の考え方が身についていると、それがかえって足かせになります。
具体的に、よくある混乱をいくつか見てみましょう。
変数の値が勝手に変わる!?
例えば、数学の文字式(代数)の頭では、次のプログラムの意味が全く理解できないはずです。
x=2
x=x+1
1行目で「xは2だ」と言っておきながら、2行目でそれを満たさない方程式が書かれています。
そもそも2行目の方程式は成立していません。
だから、意味が分からなくて混乱するでしょう。
算数や数学の=と、プログラムの=では、意味が全く違います。
それが混乱の原因です。
本に書いてあることを、よーく読まないと、こういう所で落とし穴にはまります。
初学者とは、そういう段階です。
ご存知の通り、プログラムの=は「右辺の値を左辺の変数に代入する」という意味です。
これはつまり、「次の行でxの値が変わってしまう」ことを意味します。
そして、これが混乱の原因になります。
数学では、行目と2行目が同じ文字であれば、同じ値のはずだと見なします。
値が違うのであれば、違う文字を使うからです。
それに比べると、プログラムの変数は、とても奇妙に思えます。
同じ文字なのに、1行目と2行目で値が変わってしまうのですから。
塾長が初めてプログラミングに出会ったのは中1でしたが、当時、
「xに1を足す」という式が「x=x+1」になることが気持ち悪くて、納得するまでとても時間がかかりました。
わざわざ繰り返すのはナゼ?
また「繰り返し文」(反復)の使い方にも慣れが必要でしょう。
例えば数列の問題で、1から10までの整数の合計を変数xに代入することを考えます。
数学であれば、
x=1+2+3+4+5+6+7+8+9+10
ですね。高校生なら
x=$\sum_{k=1}^{10}k$
と書いても良いでしょう。
それがプログラムになると、
x = 0
for i in range(11):
x = x+i
という表現になります。
これを日本語的に書くと、
xを0に初期化
0~10の整数を順番に変数 i に代入するたびに、
x+ i の計算結果を x に上書きで保存
という意味になります。
数学の式に比べると、なんだか面倒な手順ですよね。
計算を手順に翻訳するのに慣れが必要
このように「計算」を「手順」に翻訳する、という発想の置き換えが必要です。
つまり、プログラミングでは、これまで学校で習ってきた考え方とは異なる、独特の考え方に慣れる必要があります。
日常生活とも違う頭の使い方かもしれません。
こうした発想の置き換えには、少し訓練が必要です。
きっと偏差値の高い人でも、最初の最初は、慣れないかもしれません。
とくに独学の場合は、自分には才能がないと早とちりしてしまいます。
慣れる前に挫折してしまうかもしれません。
「これは誰でも最初はそうだよ。少し慣れが必要だよ。」
そんな助言をしてくれる人が近くにいれば、気持ちが楽になって続けられたかもしれません。
⑤(補足)関数型プログラミング言語
上で見たような課題、つまり、プログラミングの発想が数学と異なり、分かり難いという課題について、
これを解決するプログラミング言語も、あるにはあります。
数学的な発想のまま、変数や関数を使ってプログラミングができる言語です。
それは「関数型プログラミング」というパラダイムの言語です。
Haskell というプログラミング言語がその代表です。
しかし、人によっては、逆に難しい文法に見えるでしょう。
関数型プログラミングは「圏論」と呼ばれる数学が元になっているため、説明が何かと数学的で難しいです。
例えば「モナド」という代表的で必須の概念を理解するのでさえ、多くの人が挫折してしまうでしょう。
残念ながら、関数型プログラミング言語を初心者が分かりやすく学べる環境は、今のところ、ほとんどありません。
一部の才能あるプログラマや研究者たちが「簡単だよ」と言っているような状況です。
まだまだ初心者には手が出ません。
また関数型プログラミング言語は、産業界では極めてマイナーなプログラミング言語です。
関数型プログラミングができても、それで職を探すとなれば、かなり狭き門になるでしょう。
作るために学ぼう
プログラミングは体で覚えた方が早い、とよく言われます。
実際、多くの人は、本を読んだだけでは身につかないでしょう。
ちょっと書いてみて、すぐ動かして、すぐ確かめる
そういう環境を最初に作ることが、とても大切です。
そういう意味でも、スクラッチやパイソンは環境を作りやすいでしょう。
さらに、具体的に何かを作りながら学ぶと、もっと効果的です。
- 神経衰弱やジャンケンのような簡単なゲームを作ってみる
- 学校で習った数学や理科の公式をプログラムにしてみる
- エクセルの情報からグラフを作って表示するような、簡単な統計処理をしてみる
など、何か具体的に作るものを決め、それを作るために学ぶ、というスタンスにしましょう。
英語の習得は、外国人の友達をつくって、その人と会話するために学ぶのが速いらしいです。
映画や海外ドラマが好きな人は、それをネイティブに視聴するのを目的にするようです。
それと同じように、プログラミング言語を学ぶときも、
「これを作りたい」
「コンピューターをこう動かしたい」
という具体的な目標を立て、実際、すぐに作り始めるとよいでしょう。
目的と手段を分けよう
最後に、プログラミングを学ぶ上で、意外と見落としがちなポイントを1つ。
それは
「今のプログラムは手段の1つ」
ということです。
一般に、1つの目的を実現するために、取れる手段は複数あるものです。
プログラミングの方法もまた、何通りか考えられます。
答えは1つではありません。
また、今の答えが最善とも限りません。
そこが、これまで学校で学んできた5教科と決定的に違うところです。
目的を達成できれば、方法は違っていても良い!
それがプログラミングを学ぶ醍醐味と言えましょう。
そのため1度は完成したプログラムでも、
「他にも方法があるかも?」
と思案したり、他の生徒の方法を参考に、新しいアイデアを追加して改善したりできます。
それがまさに、
答えのない問題にチャレンジし、最適解を出す。
最適解を改善し、よりよい解にする。
という活動です。
もしもプログラミングの勉強が、
✖ テキストや模範解答を写すだけ
のような学びであれば、それ悲しいことです。
そのような勉強であれば、
これまで通り、5教科の勉強を頑張った方が良いでしょう。
ちょっと動かし、間違え、それを修正して、また動かしてみる。
プログラミングでは、そのようなトライ&エラーを多く経験することが、そのまま学びになります。
間違えたらバツではなく、「できるだけ前段階で多くの間違えを間違えを経験しておく」という発想に切り替えるとよいでしょう。
もっとも、これは試験対策や入試対策でも同じことですね。
あとがき
技術の世界は世代交代が速いです。
子供たちが社会に出る7年後や10年後。
その頃に、どんな技術がトレンドになっているのか、予想がつきません。
プログラミング言語も同様です。
「このプログラミング言語なら将来安心だ」というものはありません。
応用的な知識ほど、時代の流行に左右されます。
ですから就職が近いほど、その時に必要な知識を身に着けるのが良いです。
逆に言えば、まだまだ就職が遠い若い内は、流行に左右されない基礎学力を学ぶ方が良いでしょう。
それに、基礎学力のある人は、応用的な知識を独学で身に着けてしまいます。
大学生や社会人には学習塾がないでしょう。
不要だからです(不要なレベルでないと困ります)。
学校では基礎学力を学ぶのが良いと思います。
そしてプログラミングも同様です。
何の仕事に就くか分からない内から、特定の産業技術を学んでも、仕方ありません。
ですから、できるだけニュートラルなプログラミング言語で学ぶことをオススメしています。
もちろん趣味であれば、特定の産業技術でも大いに結構。
もっとも趣味であればプログラミングを「勉強する」とは言わないでしょう。
進学実績
卒塾生(進路が確定するまで在籍していた生徒)が入学した学校の一覧です。
ちなみに合格実績だけであれば更に多岐・多数にわたります。生徒が入学しなかった学校名は公開しておりません。
国公立大学
名古屋大学、千葉大学、滋賀大学、愛知県立大学、鹿児島大学
私立大学
中央大学、南山大学、名城大学、中京大学、中部大学、愛知淑徳大学、椙山女学園大学、愛知大学、愛知学院大学、愛知東邦大学、愛知工業大学、同朋大学、帝京大学、藤田保健衛生大学、日本福祉大学
公立高校
菊里高校、名東高校、昭和高校、松陰高校、天白高校、愛知教育大学附属高校、名古屋西高校、熱田高校、緑高校、日進西高校、豊明高校、東郷高校、山田高校、鳴海高校、三好高校、惟信高校、日進高校、守山高校、愛知総合工科高校、愛知商業高校、名古屋商業高校、若宮商業高校、名古屋市工芸高校、桜台高校、名南工業高校、菰野高校(三重)
私立高校
愛知高校、中京大中京高校、愛工大名電高校、星城高校、東邦高校、桜花学園高校、東海学園高校、名経高蔵高校、栄徳高校、名古屋女子高校、中部第一高校、名古屋大谷高校、至学館高校、聖カピタニオ高校、享栄高校、菊華高校、黎明高校、愛知みずほ高校、豊田大谷高校、杜若高校、大同高校、愛産大工業高校、愛知工業高校、名古屋工業高校、黎明高校、岡崎城西高校、大垣日大高校
(番外編)学年1位または成績優秀者を輩出した高校
天白高校、日進西高校、愛工大名電高校、名古屋大谷高校
※ 成績優秀者・・・成績が学年トップクラスで、なおかつ卒業生代表などに選ばれた生徒
名古屋市天白区の植田で塾を探すなら個別指導のヒーローズ!!
★ 直接のお問い合わせ ★
――――――――――――――――――――――
個別指導ヒーローズ 植田一本松校
〒468-0009
名古屋市天白区元植田1-202 金光ビル2F
TEL:052-893-9759
教室の様子(360度カメラ) http://urx.blue/HCgL