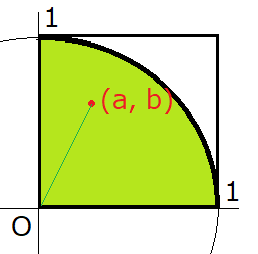塾長です。
もう春ですね。
3月3日と言えば桃の節句ですが、ことしは中学の卒業式でもあります。そのあとすぐに愛知県公立高校入試が始まります。国公立大学は先週から始まっていますね。
もう、そういう季節です。
受験が終わったら何をする?
一方で、すでに受験を終えている生徒も多いです。教室では私立高校から届いた課題に取り組む生徒たちや、中学生の総復習にあらためて取り組む生徒たちがいます。
要するに放っておけば新学期まで暇です。そんなキミたちに、
ぜひ今こそ、自分なりの「本当の勉強」というものにチャレンジしてみたらいかが?
などと声をかけています。
たとえば、理系の子には「ブルーバックス」というシリーズの本をお勧めするとか、逆に哲学の変な本を読んでみたらどうかとか、そういう雑談もしています。
コロナ禍で卒業旅行が難しい、そんなご時世だからこそ、落ち着いて本を読んでみるのも一興です。
もちろんマンガやアニメでも良いと思います。
新しい本との出会いは、新しい自分との出会いになることがあります。
また最近ではパソコンで遊んでみることもお勧めです。
塾長が生まれて初めて目にした科学計算プログラム
そんな話を生徒たちにしていたせいか、自分が高校生になったばかりの頃を急に思い出しました。
塾長は高校生になってから直ぐに地学部に入りました。天文少年だったので迷わずストレートに行きました。
高校の屋上には1つ部屋があって、その上が天文台になっていました。地学部は屋上もその部屋も天文台も、すべて自由に使うことができました。そして屋上の部屋には1台のパソコンが置いてありました。
ある日、3年生の先輩がそのパソコンで自作のプログラムを披露してくれました。
衝撃でした。何のプログラムだったか、今でもハッキリと覚えています。
モンテカルロ法による円周率の計算プログラム
今から30年以上も前です。たしかSHARPのX1というパソコンで、BASICというプログラム言語でした。
もちろんプログラムの1行1行を覚えているわけではありません。覚えているのは先輩がしてくれた説明です。
どんな計算をしているプログラムか
その仕組みというか、考え方が面白くて、今でも覚えているのです。
「あー、コンピューターって、こんなことまでできるんだ。」
そんなことを初めて実感した瞬間でした。
どんな話だったか、ちょっと説明しますね。
確率で面積を求める!?
突然ですが、もしもこんな図形があったら、どうやって面積を求めますか?
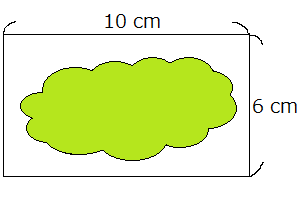
長方形の中に雲みたいな形があって、色が塗られています。その部分の面積です。
もちろん、こんな変な形の面積を出す公式なんて知りません。
こういう時に次のような発想で求められると言うのです。
確率で面積を求められる!
もう少し説明を続けます。
もしも次のことが分かれば面積が求められます。
長方形の中で雲の形が占める割合
たとえば仮に、雲の面積が長方形の面積の3分の2だとすれば、
$$ 10 \times 6 \times \frac{2}{3} = 40 cm^{2}$$
という具合に求まるわけです。つまり、
実際には何分の何なのか?
という「割合」を求められれば良いわけです。
この割合、どうやって求めましょうか?
そこで確率の登場です。
上から針を落とす実験
長方形の中で雲の形が占める「割合」を求めるために、この絵に対してランダムに点を描いていくことを考えます。
点を描く場所に偏りがあってはいけません。人間の意思が働くと偏りが出るかもしれないので、人間の意思が入らないように、でたらめにやる必要があります。例えば、この絵を地面に敷いて上から針を落とし、針の先端が止まった場所に点を描く方法などがあります。そういう方法ができたとしましょう。
試しに10本ほど針を落として、その先端に赤い印をつけてみた例が次の図です。
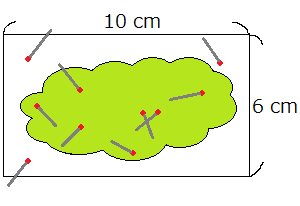
10本の針を落としたら7本が雲の図の中に入りました。つまり針が雲の中に落ちる確率が $\frac{7}{10}$ ということです。これは言い換えると、雲の面積が占める割合が長方形の $\frac{7}{10}$ だったと見なすことができます。だったら、
$$ 10 \times 6 \times \frac{7}{10} = 42 cm^{2}$$
ということで求めたことになりそうです。
良ろしいでしょうか?
けっこう良い線まで求められたとは思いますが、まだ不安ですよね。
たったの10本で決断してよいの?
そういう不安感があるからです。たまたま7本だったのかもしれません。もう1回実験したら $\frac{6}{10}$ になったり、 $\frac{8}{10}$ になったりするかもしれません。
10回では自信が持てないのなら回数を増やせばよいです。そこで1万回くらい実験しましょう。そしてその結果が、 $\frac{6711}{10000}$ になったとします。だったら、
$$ 10 \times 6 \times \frac{6711}{10000} = 40.266 cm^{2}$$
ということで良いでしょうか?
かなり良い線まで求められたとは思います。
しかし、まだ不安が0ではないですよね。1万回よりは10万回、いや100万回。いやいや1億回なら・・・などと増やしていけば、いつかは求まるだろうと思うワケです。
このようにランダムな行為で発生する確率を利用して、何かを計算していく方法を「モンテカルロ法」と呼びます。
この発想法、すごくないですか?
塾長は高1の春に感動した思い出があります。
ところで、円の面積も、これと同じ方法で求めることができます。そして円の面積が分かれば円周率も分かるというワケです。
確率で円の面積を求める!
それでは円の面積を求めていきましょう。
いま半径1の円を描きます。中心を座標の原点にすると下の図のようになります。
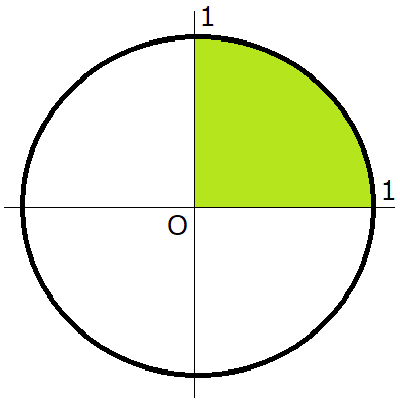
ここでマイナスの座標を使うと計算が面倒です。そこでx座標もy座標も「正の数」だけ使うことにします。それが図で黄緑色の部分です。
つまり下図のように円の右上4分の1の扇形だけを実験に使います。
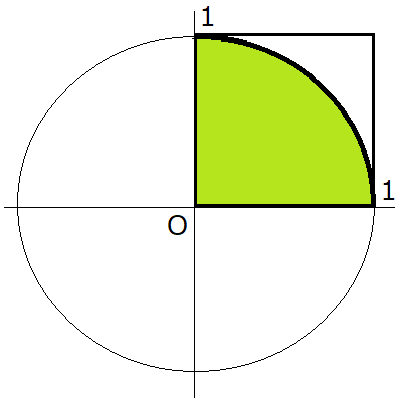
この図で色のついた扇形は、1辺が1の正方形の中にピタリと納まっています。この正方形の中に針を落とす実験をしてランダムに点を打っていきましょう。すると
$$半径1の円の\frac{1}{4}の面積=1 \times 1 \times \frac{扇の中の点の数}{点の総数} =\frac{扇の中の点の数}{点の総数} $$
となりますね。
一方で円の面積の公式を使った式では、
$$半径1の円の\frac{1}{4}の面積=1 \times 1 \times \pi \times \frac{1}{4} = \frac{\pi}{4} $$
両者は同じはずですから、
$$ \frac{扇の中の点の数}{点の総数}=\frac{\pi}{4} $$
よって
$$ \pi = 4 \times \frac{扇の中の点の数}{点の総数}$$
となって円周率 $\pi$ が求まるわけです。
プログラミングで求める!
それでは上の考えをプログラミングします。
ちなみに正しい円周率は、
$$\pi=3.1415926535 \dots$$
だそうです。
今回はこれを模範解答として、プログラミングで得られた円周率の精度を評価してみましょう。
扇の中か外かの判定は?
プログラミングをする上で、あと1つ問題が残っています。それは
打たれた点が「扇の中か外かを判定する計算」をどう実現するか?
という問題です。
先に答えを言ってしまうと、これは中3の「三平方の定理」で解決します。
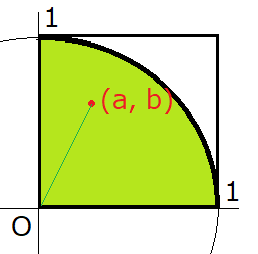
例えば上のように点が打たれたとします。もしもその座標が $(a, b)$ だったとすれば、原点からその点までの距離は三平方の定理から $\sqrt{a^{2}+b^{2}}$ となります。これが円の半径1よりも小さければ扇形の内部というワケです。
ただし1は2乗してもしなくても1なので、 $\sqrt{a^{2}+b^{2}}$ の代わりに $a^{2}+b^{2}$ を使っても、1以上か未満かの判定には影響しません。少しでも計算を楽にしてあげた方がコンピューターから高速に結果を得られます。そこでプログラムではルートを取る前の $a^{2}+b^{2}$ と1を比べて判定します。
さぁ、今度こそプログラミングです。
まずは私が高校生の時に経験したBASICというプログラミング言語で再現してみます。
BASICのプログラミング
半径1の図をそのまま描くと小さすぎて何も見えなくなるので、400倍に拡大して描画するようにプログラミングしています。
10 CLS
20 DEFINT L
30 L=400:COUNT=0:R=0.0:X=0.0:Y=0.0
40 CIRCLE(0,0),L,1
50 LINE(L,0)-(L,L)
60 LINE(0,L)-(L,L)
70 INPUT N
80 FOR I=1 TO N
90 X=RND(1)
100 Y=RND(1)
110 PSET((L*x),(L*Y)),2
120 R=X*X+Y*Y
130 IF R <= 1.0 THEN COUNT=COUNT+1
140 NEXT I
150 PRINT (4*COUNT/N)
このプログラムを使って、針を落とす実験の回数を10000回まで実行したのが下の図です。この1万回の実験で、だいたい6秒くらいかかりました。
扇形は青い線で、針の落ちた場所が赤い点です。
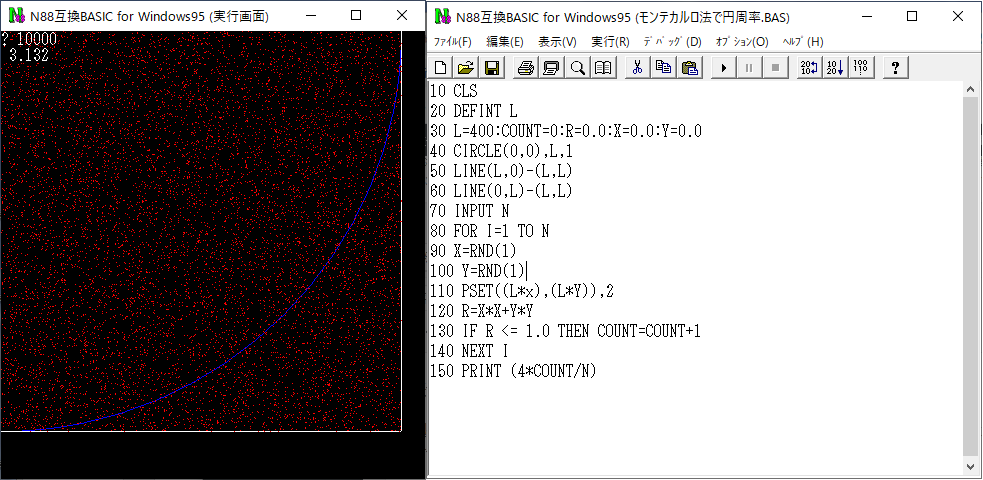
円周率が3.132と出ています。
残念ながら1万回の実験をもってしても小数第1位くらいまでしか求まらなかったようです。
そこで10万回に増やしてみました。今度は60秒くらいかかりました。

10万個も点を打つと、かなり塗りつぶされている感じになります。
そして円周率が3.1404と出ています。
ようやく10万回でお馴染みの「3.14」つまり小数第2位まで求められました。
こりゃ、とてもじゃないけど、人間の手で実験なんてしていられませんね。
Pythonのプログラミング
今度は同じことを「Python(パイソン)」というプログラミング言語で実行しました。下がそのプログラムです。
BASICよりも高速に動作するので、10万回を超えるような計算はPythonの方で実験することにします。
グラフィックは面倒なので省略します。その代わり計算にかかった時間を表示するようにしました。
import random as r
import time as t
def cal_pai(n):
count_in = 0
start = t.time()
for i in range(n):
x = r.random()
y = r.random()
if (x*x + y*y) <= 1:
count_in += 1
pai_n = 4*count_in/n
print(“n={}, pai={}, time={}[sec]”.format(n, pai_n, (t.time()-start)))
cal_pai(100)
cal_pai(1000)
cal_pai(10000)
cal_pai(100000)
cal_pai(1000000)
cal_pai(10000000)
cal_pai(100000000)
cal_pai(1000000000)
実行結果が下の図です。私のパソコンでは1億回の計算に21秒くらい、10億回の計算に4分12秒くらいかかりました。
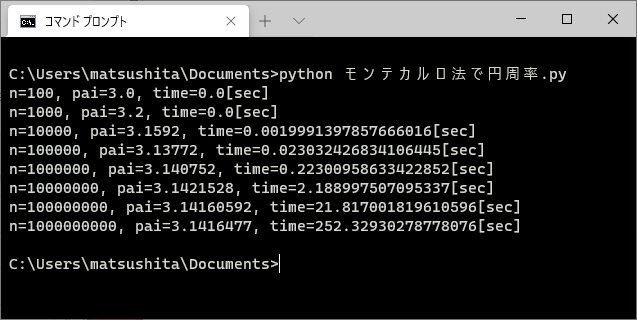
なるほど、やっぱり10万回で「3.14」まで求まるようですね。
そして1億回で小数第3位の3.141まで求まっています。
しかし10億回に増やしても小数第4位まで出すことができませんでした。本当は3.1415…と表示されて欲しいのですが、3.1416…となっています。
そこで100億回にチャレンジしてみたいところですが、そうすると1時間くらいかかりそうなので止めておきます。
Scratch(スクラッチ)のプログラミング
最後にスクラッチのプログラミングです。
スクラッチは計算が遅いので、このように何千万回も計算をするような処理には向きません。ただしプログラムは読みやすいです。
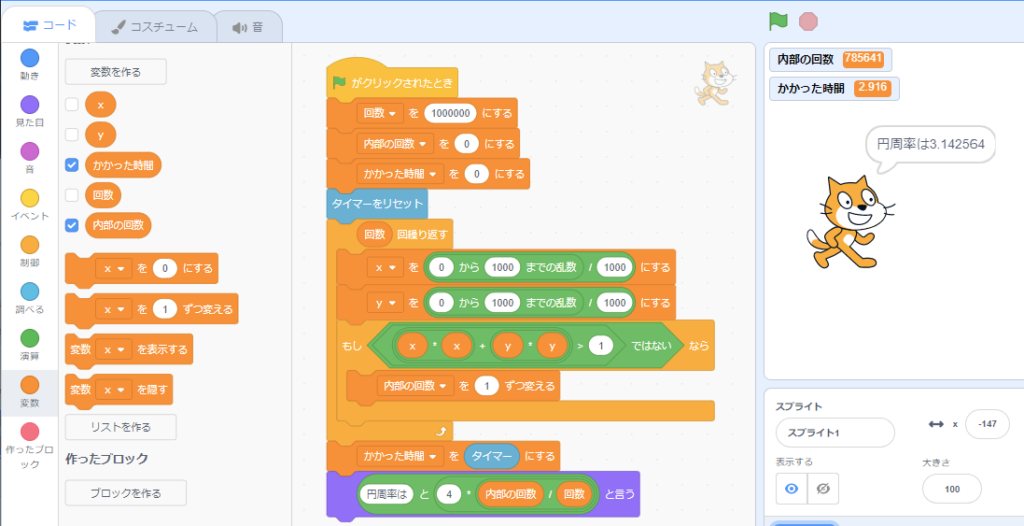
実行してみると100万回で小数第2位の3.14まで求まりました。かかった時間は3秒弱でした。意外と速いですね!
同じ100万回で見ると、Pythonは約0.22秒、BASICは約600秒ですから、スクラッチの計算速度はBASICの200倍、Pythonの$\frac{1}{13}$くらいの速さということになりました。もっとも今回のBASICはエミュレーター上で動作し、なおかつグラフ表示もしているため遅いのは仕方がありません。
スクラッチは簡単にプログラミングできる環境でありながら、立派にアルゴリズムをプログラミングして実験できる環境だと言えます。
小学生が初めてプログラミングする環境として「スクラッチが最強」であることが、あらためて実感できました。
弱点を補うのもプログラミング
スクラッチにも弱点はあります。今回のプログラムに関しては次の2つです。
- 小数の乱数を生み出す命令が無い
- 「以上」「以下」を表す演算子が無い(「より大きい」「より小さい」しかない)
この2つの弱点を補うために、それぞれ次のような工夫しています。
- 「0~1000の範囲」で整数の乱数を生成し、それを1000で割って小数にした
- 「1以下のとき」の条件が作れないので、代わりに「「1より大きい」でないとき」とした
みなさんならどのように工夫しますか?
有るもので工夫するのもプログラミング的思考の大切なポイントです。
とても奥が深い分野
モンテカルロ法は奥がとても深くて、大学の卒業論文などでもよく取り上げられる問題です。
奥が深いとは、例えば、実際に実験することを想像すればわかります。
実際に実験するときには、先に実験の目的を決めますよね。今回なら
「円周率を小数第何位まで求めたいか?」
ということを決めます。
仮に、これが世界で初めての実験だったとしましょう。
すると逆に、
「その桁まで求めるには、何回くらい実験する必要があるのか?」
ということが分かっていなければ、実験を終わらせることができません。
世界で初めて実験するのですから、まだ誰も円周率の小数第4位の数を知りません。つまり正解が分かっていません。
答え合わせができない!
というのが、この実験の難しいところなのです。
そこで代わりに
「何回目の実験で正解にたどり着けるのか?」
を何らかの方法で求めておく必要があります。
それが分かっていなければ、いつまでもゴールできません。永遠に実験をし続ける羽目になってしまいますから。
この「実験を終えてよい回数」を求める方法は、実はとても難しい理論になります。大学の数学レベルの話になってしまいます。
上の実験では、Pythonで10億回やっても小数第4位を正しく出せんでした。しかし実際の実験では、そもそも「正しく出なかった」という判断ができません。今回は先に円周率の正解を表示するという「ズル」をしていたので「まだ求まっていない」という判断ができた、というワケです。
さて、円周率の小数第4位の数。
100億回なら出るのでしょうか?
もしかしたら1000億回なのでしょうか?
こういうたいへんな作業をやる前に、先に「何回やったら終わっていいよ。」という回数を知っておきたいですね。
大学受験の範囲を超えてしまいますが、興味のある人は調べてみてください。
暇な時間を上手に使える人に成ろう
高校受験や大学受験を終えた皆さんが、暇つぶしをするネタとして、今回はモンテカルロ法で円周率を求めるプログラミングを提供してみました。
塾長の過去の思い出から、たまたま思い出したので書いてみました。
コンピューターを使った遊び方は色々ですが、ゲームをするだけではもったいないです。
ぜひコンピューターが持つ本当の力を引き出してみてください。
もちろん、これは時間の使い方の1つの例です。
みなさんは暇な時間に何をしますか?
そういう時間を上手に使える人に成りたいものですね。
ヒーローズ植田一本松校の進学実績
卒塾生(進路が確定するまで在籍していた生徒)が入学した学校の一覧です。
ちなみに合格実績だけであれば更に多岐・多数にわたりますが、当塾の理念に反するので生徒が入学しなかった学校名は公開しておりません。
国公立大学
名古屋大学、千葉大学、滋賀大学、愛知県立大学、鹿児島大学
私立大学
中央大学、南山大学、名城大学、中京大学、中部大学、愛知淑徳大学、椙山女学園大学、愛知大学、愛知学院大学、愛知東邦大学、同朋大学、帝京大学、藤田保健衛生大学、日本福祉大学
公立高校
菊里高校、名東高校、昭和高校、松陰高校、天白高校、名古屋西高校、熱田高校、緑高校、日進西高校、豊明高校、東郷高校、山田高校、鳴海高校、三好高校、惟信高校、日進高校、守山高校、愛知総合工科高校、愛知商業高校、名古屋商業高校、若宮商業高校、名古屋市工芸高校、桜台高校、名南工業高校
私立高校
中京大中京高校、愛工大名電高校、星城高校、東邦高校、桜花学園高校、東海学園高校、名経高蔵高校、栄徳高校、名古屋女子高校、中部第一高校、名古屋大谷高校、至学館高校、聖カピタニオ高校、享栄高校、菊華高校、黎明高校、愛知みずほ高校、豊田大谷高校、杜若高校、大同高校、愛産大工業高校、愛知工業高校、名古屋工業高校、黎明高校、岡崎城西高校、大垣日大高校
(番外編)学年1位または成績優秀者を輩出した高校
天白高校、日進西高校、愛工大名電高校、名古屋大谷高校
※ 成績優秀者・・・成績が学年トップクラスで、なおかつ卒業生代表などに選ばれた生徒
生徒・保護者様のお友達登録はこちら
LINE登録するとプレゼントがもらえます!
【会員限定】お子様の成績と可能性を伸ばす18個のノウハウ

塾関係者様のお友達登録はこちら
LINE登録するとプレゼントがもらえます!
「zoomで簡単。オンライン授業移行の教科書」
または個別対談も可

名古屋市天白区の植田で塾を探すなら個別指導のヒーローズ!!
★ 直接のお問い合わせ ★
――――――――――――――――――――――
個別指導ヒーローズ 植田一本松校
〒468-0009
名古屋市天白区元植田1-202 金光ビル2F
TEL:052-893-9759
教室の様子(360度カメラ) http://urx.blue/HCgL