塾長です。
昨日は公立高校入試B日程の学科試験でした。今日の面接試験で愛知県の高校入試がひと段落します。
さて前回に引き続き、B日程の数学についても解説をつくりました。
中学2年生までの知識でも半分くらいは解ける問題です。あとの半分は中学3年生になってからチャレンジしてみましょう。
さっそく植田中学では、2年生にA日程の問題を解かせて授業中に解説してくれたみたいです。流石です。
学校の授業中で消化しきれなかった入試問題について、生徒たちから質問が来るようになりました。このブログが家庭学習にも役立てば幸いです。
そのため、できるだけ発想や考え方の過程についても書いておきました。
【1】次の(1)から(10)までの問に答えなさい。
(1)【中1】 $3−7\times (5−8)$ を計算しなさい。
$3−7\times (5−8)$
$=3-7\times (-3)$
$=3+21=24$
(2)【中2】 $27x^{2}y\div (-9xy)\times (-3x)$ を計算しなさい。
$27x^{2}y\div (-9xy)\times (-3x)$
$=\frac{27x^{2}y\times (-3x)}{-9xy}$
$=\frac{27\times 3\times x^{3}y}{9xy}$
$=9x^{2}$
(3)【中3】 $\sqrt{48}-3\sqrt{6}\div\sqrt{2}$ を計算しなさい。
$\sqrt{48}-3\sqrt{6}\div\sqrt{2}$
$=\sqrt{4^{2}\times 3}-3\sqrt{\frac{6}{2}}$
$=4\sqrt{3}-3\sqrt{3}$
$=\sqrt{3}$
(4)【中3】 $(x+1)(x-8)+5x$ を因数分解しなさい。
$(x+1)(x-8)+5x$
$=x^{2}+(1-8)x-8+5x$
$=x^{2}-7x+5x-8$
$=x^{2}-2x-8$
$=(x-4)(x+2)$
(5)【中3】 方程式 $(x+2)^{2}=7$ を解きなさい。
$(x+2)^{2}=7$
$x+2=\pm \sqrt{7}$
$x=-2\pm \sqrt{7}$
(6)【中1】 $\ a\ $個のあめを10人に$\ b\ $個ずつ配ったところ、$\ c\ $個余った。
この数量の関係を等式に表しなさい。
$a=10b+c$
($10b+c=a$)
($b=\frac{a-c}{10}$)
($\frac{a-c}{10}=b$)
($c=a-10b$)
($a-10b=c$)
($10b=a-c$)
($a-c=10b$)※「$a\ を\ b,\ c\ $で表せ」などの指定がないため、上記のどれでも正解
(7)【中1】 男子生徒8人の反復横跳びの記録は、次のようであった。
$$53\ 45\ 51\ 57\ 49\ 42\ 50\ 45\ (単位:回)$$
この記録の代表値について正しく述べたものを、次のアからエまでの中からすべて選んで、そのかな符号を書きなさい。
ア 平均値は、49回である。
イ 中央値は、50回である。
ウ 最頻値は、57回である。
エ 範囲は、15回である。
ア 平均値は、$\frac{(53+45+51+57+49+42+50+45)}{8}=\frac{392}{8}=49\ $回だから〇
イ 中央値は、資料を並び替えれば$\ 42\ 45\ 45\ 49\ 50\ 51\ 53\ 57\ $であるから$\ \frac{49+50}{2}=49.5\ $回となって×
ウ 最頻値は、$\ 45\ $回だから×
エ 範囲は、最大値-最小値$=57-42=15\ $回であるから〇以上から
ア、エ
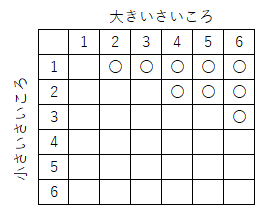
(8)【中2】 大小2つのさいころを同時に投げる時、大きいさいころの目の数が小さいさいころの目の数の2倍以上となる確率を求めなさい。
全ての出目の組み合わせについて表で確認すれば、下図のようになる。
よって、$\frac{9}{36}=\frac{1}{4}$
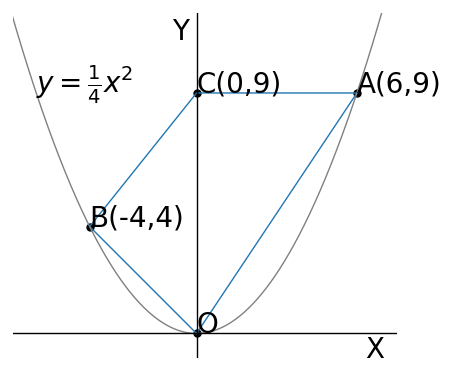
(9)【中3】 関数$\ y=ax^{2}\ (a\ は定数)$と$\ y=6x+5\ $について、$\ x\ $の値が1から4まで増加するときの変化の割合が同じであるとき、$\ a\ $の値を求めなさい。
<解法1>
定義通りに式を立てる。
関数$\ y=ax^{2}\ $の変化の割合は$\ \frac{y\ の増加量}{x\ の増加量}\ $であり、$\ y=6x+5\ $のそれは傾き$\ 6\ $のことであるから、
$\frac{a\times 4^{2}-a\times 1^{2}}{4-1}=6$
$\frac{16a-a}{3}=6$
$\frac{15a}{3}=6$
$5a=6$
$a=\frac{5}{6}$<解法2>
関数$\ y=ax^{2}\ $の変化の割合は、公式を使えば$\ (1+4)a=5a\ $であるから、
$5a=6$
$a=\frac{5}{6}$
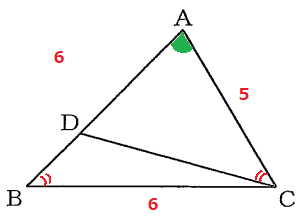
(10)【中3】 図で、Dは$\triangle ABC\ $の辺AB上の点で、∠DBC=∠ACDである。
AB=$6 cm\ $、AC=$5 cm\ $のとき、線分ADの長さは何$cm\ $か、求めなさい。
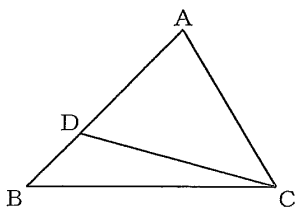
題意から分かることを図に書き込む。
すると、$\triangle ABC\ $と$\triangle ACD\ $が相似であると分かる。
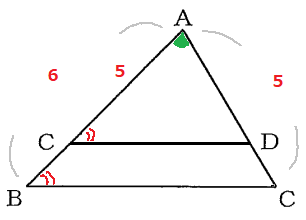
なぜなら、共通の角だから∠BAC=∠CADとなり、題意の∠DBC=∠ACDと合わせて「2角が等しい」からである。
$\triangle ACD\ $の三角形の向きを左右ひっくり返して向きをそろえて重ねると、もっと分かりやすい。
よって、求める線分ADを$\ x\ $とすれば、
$6:5=5:x$
$6x=25$
$x=\frac{25}{6}\ cm$
【2】次の(1)から(3)までの問に答えなさい。
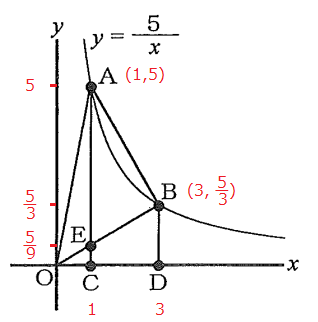
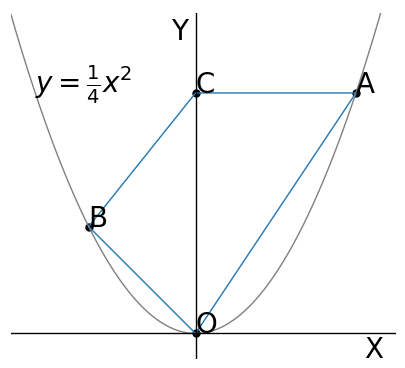
(1)【中2】 図で、Oは原点、A、Bは関数$\ y=\frac{5}{x}\ $のグラフ上の点で、点A、Bの$\ x\ $座標はそれぞれ1、3であり、C、Dは$\ x\ $軸上の点で、直線AC、BDはいずれも$\ y\ $軸と平行である。また、Eは線分ACとBOとの交点である。
四角形ECDBの面積は$\triangle$AOBの面積の何倍か、求めなさい。
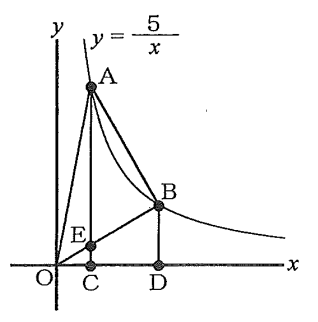
題意から分かる値を図に書き込む。
AとBの座標は、$\ y=\frac{5}{x}\ $に$x=1,\ 3\ $をそれぞれ代入して求められる。
またEの座標は、直線OBの変化の割合を計算すれば求められる。それは
$\ \frac{5}{3}\div 3$
$=\frac{5}{3}\times \frac{1}{3}$
$=\frac{5\times 1}{3\times 3}$
$=\frac{5}{9}$
よって直線OBの式は
$y=\frac{5}{9}x$
とわかる。これに$\ x=1\ $を代入すればよい。(※)「変化の割合」とは「$\ x\ $が1増加した時の$\ y\ $の増加量」だから、計算しなくても$\ \frac{5}{9}\ $がそのままEの高さになると分かる。
(※)$\triangle$OBDと$\triangle$AECの相似比から$\ BD\times \frac{1}{3}\ $と計算してもよい。図から、BD=$\frac{5}{3}$、ECD=$\frac{5}{9}$、CD=2であるから、四角形ECDBの面積は、台形の面積の公式より
$(\frac{5}{3}+\frac{5}{9})\times 2\times{1}{2}$
$=\frac{15}{9}+\frac{5}{9}$
$=\frac{20}{9}$$\triangle$AOB=四角形CDBA+$\triangle$OCA-$\triangle$ODB
$=(\frac{5}{3}+5)\times 2\times \frac{1}{2}+5\times 1\times\frac{1}{2}-3\times\frac{5}{3}\times \frac{1}{2}$
$=\frac{5}{3}+\frac{15}{3}+\frac{5}{2}-\frac{5}{2}$
$=\frac{10}{6}+\frac{30}{6}+\frac{15}{6}-\frac{15}{6}$
$=\frac{40}{6}$
$=\frac{20}{3}$以上から
$\frac{20}{9}\div \frac{20}{3}$
$=\frac{20}{9}\times \frac{3}{20}$
$=\frac{1}{3}\ $倍―――【割合の復習】―――
「〇は△の◇倍」⇔「〇÷△=◇」
だったから、
「四角形ECDBの面積は$\triangle$AOBの面積の何倍か」
は
[四角形ECDBの面積]÷[$\triangle$AOBの面積]
である。
(2)【中1】 次の文章は、連続する2つの自然数の間にある、分母が5で分子が自然数である分数の和について述べたものである。
文章中の【Ⅰ】、【Ⅱ】、【Ⅲ】にあてはまる数をそれぞれ書きなさい。また、【Ⅳ】にあてはまる式を書きなさい。
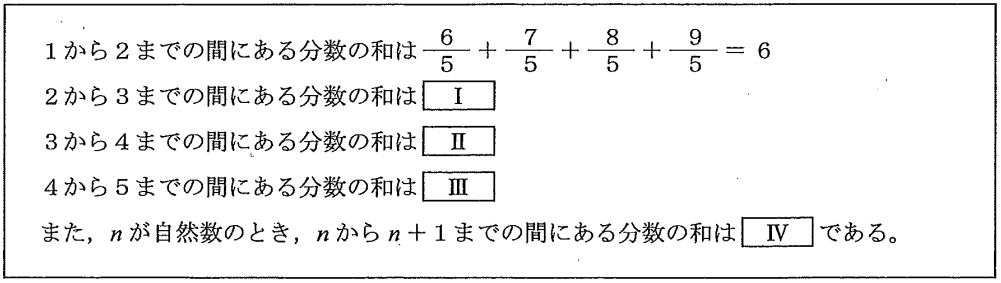
まず問題文の意味を理解していこう。
「連続する2つの自然数の間にある、分母が5で分子が自然数である分数の和」
さらりと読んだだけでは何を言っているのか分からない。数学には数学専用の読解力が必要で、特にこういう問題はその訓練量が試される。こういうときは手を動かして、具体的な例で考えてみるに限る。
そして問題文の□囲みの中に、その様子が書かれているので、言われた通りに順を追って考えていこう。まず「1から2までの間」で考えてみる。しかも「分母が5」であることに注意する。
まず1を分数にすると$\ \frac{5}{5}\ $で、2を分数にすると$\ \frac{2\times 5}{5}\ $である。
よって「1と2の間で分母が5の分数の和」は、
$\ \frac{5}{5}+\frac{6}{5}+\frac{7}{5}+\frac{8}{5}+\frac{9}{5}+\frac{10}{5}\ $
である。
いや、ちがう。
「間」だから両端を含んではいけない。
だから、
$\ \frac{6}{5}+\frac{7}{5}+\frac{8}{5}+\frac{9}{5}\ $
となっている。
ここで分母がすべて5なのだから、分母は1つにまとめられる。要するに
$\ \frac{6+7+8+9}{5}\ $
とすれば分子だけ考えれば良くなる。この時点で分子の数の並びが、
「1×5と2×5の間(ただし1×5と2×5自身は含まない!)」
となっていることに気付けば、あとは楽になる。
ここまでが第1関門。次に問題の「2から3までの間」。上と同様に考えれば、分子の並びは
「2×5と3×5の間(ただし2×5と3×5自身は含まない!)」つまり
「10と15の間(ただし10と15自身は含まない!)」
となるから、
$\frac{11+12+13+14}{5}$
$=\frac{50}{5}$
$=10\ $【Ⅰ】ちなみに分子の計算を
$11+12+13+14$
$=10+10+10+10+1+2+3+4$
$=10*4+(1+4)+(2+3)$
$=40+10$
$=50$
などと工夫できたら暗算が楽になる。同様に「3から4までの間」では分子が「16から19」だから
$\frac{16+17+18+19}{5}$
$\frac{10\times 4+(6+9)+(7+8)}{5}$
$=\frac{40+15+15}{5}$
$=\frac{70}{5}$
$=14\ $【Ⅱ】「4から5までの間」では分子が「21から24」だから
$\frac{21+22+23+24}{5}$
$\frac{20\times 4+(1+4)+(2+3)}{5}$
$=\frac{80+5+5}{5}$
$=\frac{90}{5}$
$=18\ $【Ⅲ】ここで分子の項は4つだけであることに注意しよう。よって、
「$\ n,\ (n+1)\ $の間」のときは
$\frac{n\times5 +1\ +\ n\times 5+2\ +\ n\times 5+3\ +\ n\times 5+4\ }{5}$
$=\frac{n\times5 \times 4+(1+4)+(2+3)}{5}$
$=\frac{20n+5+5}{5}$
$=\frac{20n+10}{5}$
$=\frac{5(4n+2)}{5}$
$=4n+2\ $【Ⅳ】
(3)【中2】 Aさんが使っているスマートフォンは、電池残量が百分率で表示され、0%になると使用できない。このスマートフォンは、充電をしながら動画を視聴するとき、電池残量は4分あたり1%増加し、充電せずに動画を視聴するとき、電池残量は一定の割合で減少する。
Aさんは、スマートフォンで1本50分の数学講座の動画を2本視聴することにした。
Aさんは、スマートフォンの充電をしながら1本目の動画を視聴しはじめ、動画の視聴をはじめてから20分後に充電をやめ、続けて充電せずに動画を視聴したところ、1本目の動画の最後まで視聴できた。
スマートフォンの電池残量が、Aさんが1本目の動画の視聴をはじめたときは25%、1本目の動画の最後まで視聴したときはちょうど0%であったとき、次の①、②の問に答えなさい。
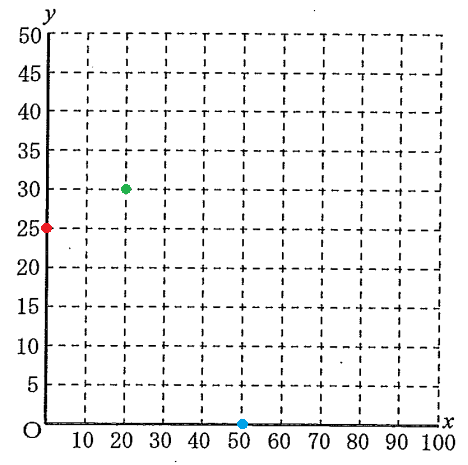
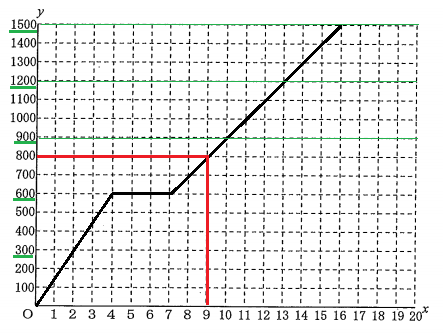
①【中2】 Aさんが1本目の動画を視聴しはじめてから$\ x\ $分後の電池残量を$\ y\ $%とする。Aさんが1本目の動画の視聴をはじめてから1本目の動画の最後まで視聴するまでの、$\ x\ $と$\ y\ $の関係をグラフに表しなさい。
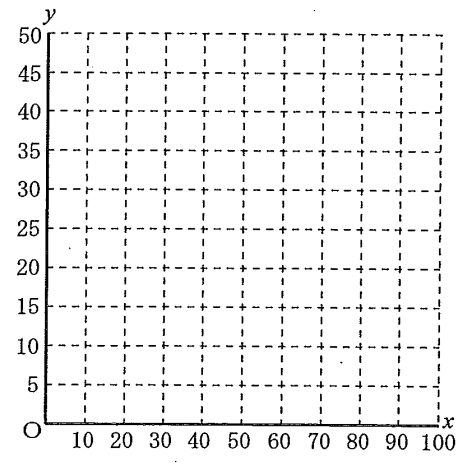
これまた情報量が多いので、必要な情報を探しながらグラフに描いていく。
ちなみに、グラフは$\ x\ $軸に沿って左から右へ描いていくのが基本である(関数は$\ x\ $を決めたら$\ y\ $が1つ定まる、という定義であり、その関数の様子を図示したのがグラフだから)。$\ x\ $軸は経過時間(分)を表しているから、まず0分の時点から考えよう。
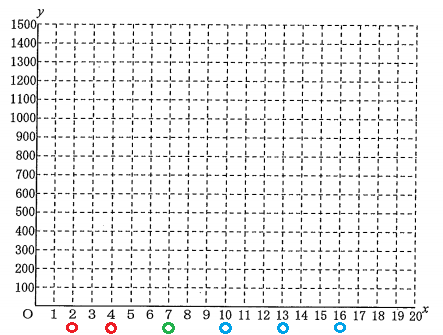
文脈から0分時点の電池残量は25%だったとあるので(0,25)に印をつけよう。
次に傾き(変化の割合)を知る必要がある。そうしなければ、右のどこの点を打てるのかが決まらない。
文脈から0~20分は充電しながら視聴していたので、電池が増減する変化の割合は、「電池残量は4分あたり1%増加」があてはまる。
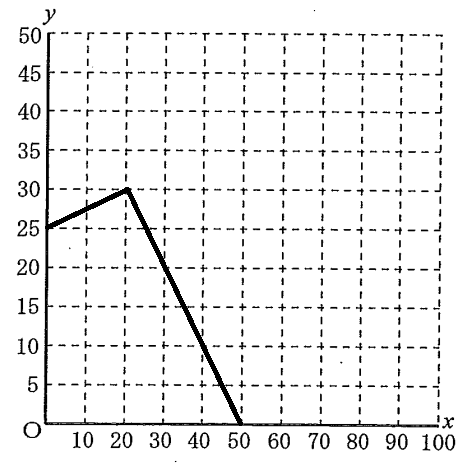
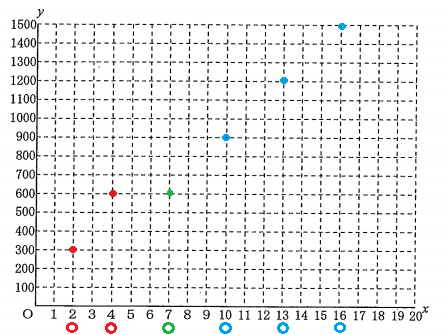
「4分で+1%」ということは「20分で+5%」であるから、電池残量は20分目では30%になっているはずである。よって(20,30)に印をつけよう。そして「1本目の動画の最後まで視聴したときはちょうど0%」とある。動画の長さは50分だったらか(50,0)に印をつけよう。
これらを線で結べばよい。
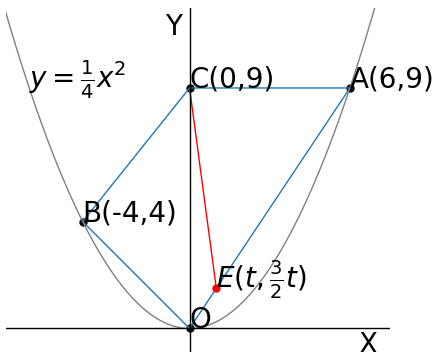
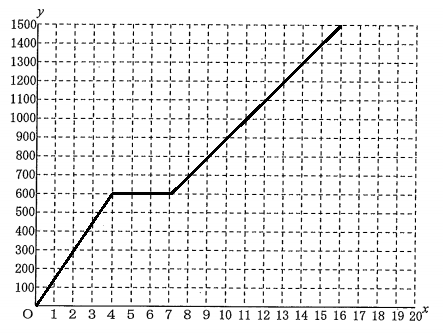
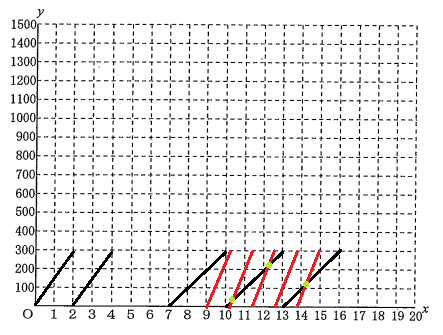
②【中2】 Aさんが1本目の動画の最後まで視聴したのち、2本目の動画の最後まで視聴するためには、2本目の動画はスマートフォンの充電をしながら何分以上視聴すればよいか、求めなさい。
これは逆算で考えていく。
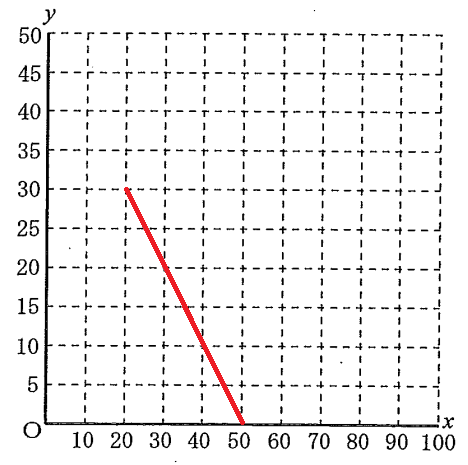
つまり2本目の動画を見終わったときに電池残量が0%になるのが最低条件であるから、そこから逆算する。上の問から、充電せずに動画を視聴した場合の変化の仕方は、グラフの20~50分の部分であった。2本目の動画も50分間だから、この部分はこのまま使える。
そして2本目の動画を見はじめた時は電池残量が0%である。つまり0分目は0%から出発する。つまり原点から出発する。
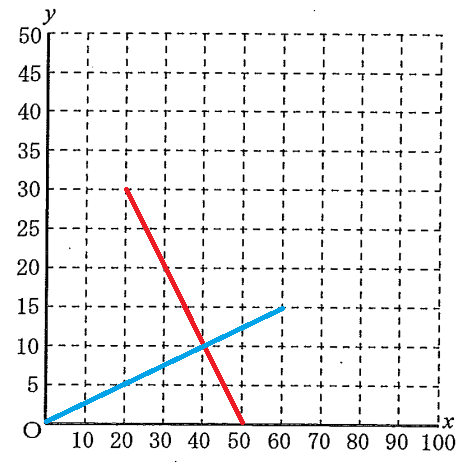
充電しながら見るのだから、変化の割合は「電池残量は4分あたり1%増加」。これは「20分で+5%」だったから、20分ごとに5%ずつ上昇するグラフになる。
よって、赤いグラフと青いグラフの交点のときが求める時間である。計算せずともグラフから読み取れば40分である。よって
40分以上
【3】次の(1)から(3)までの問に答えなさい。
ただし、答えは根号をつけたままでよい。
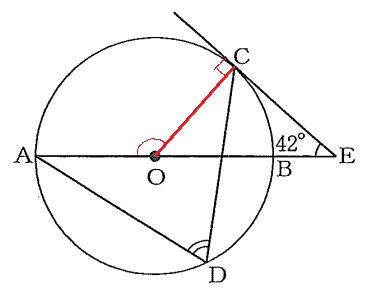
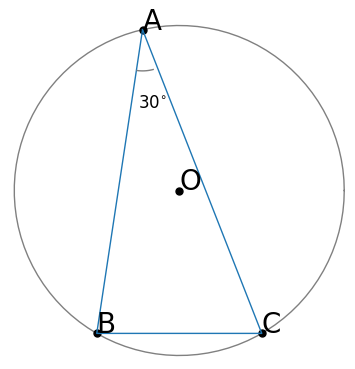
(1)【中3】 図で、C、DはABを直径とする円Oの周上の点、Eは直線ABと点Cにおける円Oの接線との交点である。
∠CEB=$42^{\circ}\ $のとき、∠CDAの大きさは何度か、求めなさい。
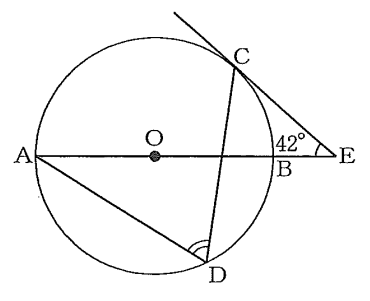
―――<解法1>―――
※ この解法1は「個別学習のセルモ 日進西小学校前教室」の西尾先生からご提供ただきました。ぜひ西尾先生のブログもご参照くださいませ。
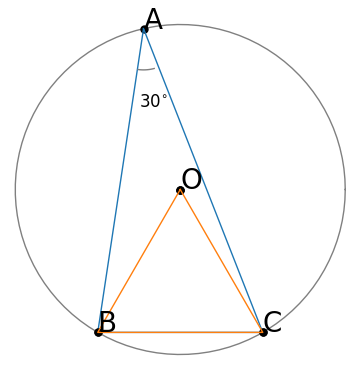
接線が引かれているので、円の接線の性質「中心から接点に引いた半径は、接線と垂直」を使えないだろうかと考えて補助線を引いてみる。
外角の公式より、∠AOC=∠OCE+∠CEO=$90^{\circ}+42^{\circ}=132^{\circ}$
円周角の定理「中心角は円周角の2倍」より、
∠CDA=∠AOC÷2=$132^{\circ}\div 2=66^{\circ}$
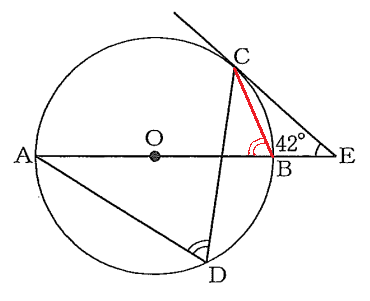
―――<解法2>―――
求める∠CDAは円周角であるから、円周角の定理を使うことを考える。そこでDを円周上のどこかに移動すると解けるかもしれないと考えて補助線を引いてみる。
またCが接点であるから、円の接線の性質「中心から接点に引いた半径は、接線と垂直」を使えないだろうかと考えて補助線を引いてみる。
すると、OBとOCはともに半径だから二等辺三角形ができる。「二等辺三角形は底角が等しい」が使えそうである。
$\triangle$OECについて、
∠COE$=180^{\circ}-42^{\circ}-90^{\circ}=48^{\circ}\ $だから、
∠OBC=$(180^{\circ}-48^{\circ})\div 2=66^{\circ}$∠CDA=∠OBC=$66^{\circ}$
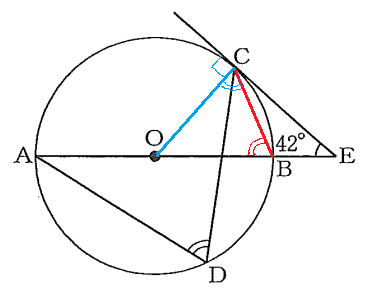
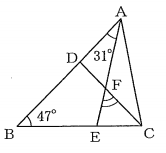
―――<解法3>―――
※ この解法3および下の図は、大阪の「あおい塾」の神田先生からご提供いただきました。大阪方面の方は神田先生のブログもぜひチェックしてみてください。
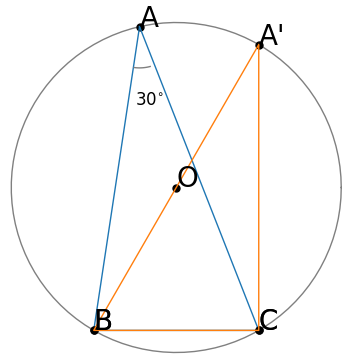
∠ADCが円周角であるから、Dを円周上で動かして利用しやすくなるように考える。角度がわっている∠BECに近づけたら何かあるだろうと考えて、DをBまで動かしてみよう。
そう考えて補助線BCをひく。
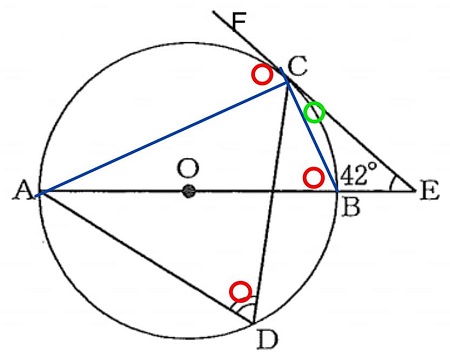
次に「接弦定理」を思い出して、これを利用してみようと思いつく。そう考えて補助線ACをひく。
円周角の定理から∠ADC=∠ABC、かつ、∠ACB=$90^{\circ}$
接弦定理より∠ACF=∠ABCまず接線上の角度の合計は$180^{\circ}$だから、
[緑の〇]+$90^{\circ}$+[赤の〇]=$180^{\circ}$
整理して
[緑の〇]+[赤の〇]=$90^{\circ}$ …①
∠ABCが$\triangle$BECの外角だらか、外角の公式を使って
[緑の〇]+$42^{\circ}$=[赤の〇] …②①と②を連立方程式のように解けばよい。[赤の〇]を出すのが目的だから①-②で[緑の〇]を消すのが良い。
式①-式②より
[赤の〇]-$42^{\circ}$=$90^{\circ}$-[赤の〇]
2×[赤の〇]=$90^{\circ}+42^{\circ}$=$132^{\circ}$
[赤の〇]=$66^{\circ}$
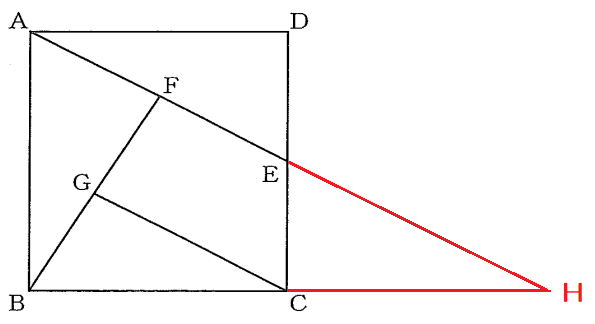
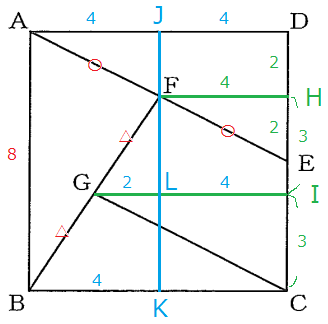
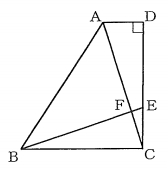
(2)【中3】 図で、四角形ABCDは正方形であり、Eは辺DCの中点、Fは線分AEの中点、Gは線分FBの中点である。
AB=$8\ cm\ $のとき、次の①、②の問に答えなさい。
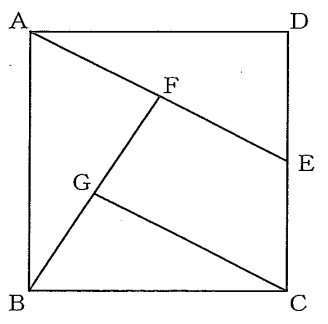
①【中3】 線分GCの長さは何$\ cm\ $か、求めなさい。
―――<解法1>―――
やたらと中点が多いので「中点連結定理」を使えないだろうかと考える。
中点連結定理に必要なのは、①三角形
②1辺に中点
③中点から伸びる底辺に平行な線の3つである。
これらの条件をGCの周りでそろえていけば解けそうである。まず②としてFBの中点Gがある。すると③はGCとなりそうだ。ならばFEが底辺になりそうだが、①の形が未完成。
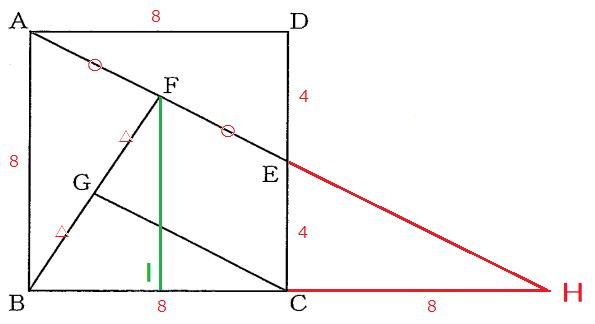
そこで次のように補助線を引く。
AEをEの方へ延長し、またBCをCの方へ延長し、その交点をHとした。
するとパッと見は$\triangle$BFHで中点連結定理のような図形になった。本当にそうか確かめよう。まず、$\triangle$ADE≡$\triangle$HCE
となるから、AD=CH=BCとなる。つまりCはBHの中点と分かる。
よって中点連結定理より、$GC\ //\ FH$であり、同時に
$GC=\frac{1}{2}FH$
である。
確かに中点連結定理の形になっている。だから、あとはFHを求めればよい。
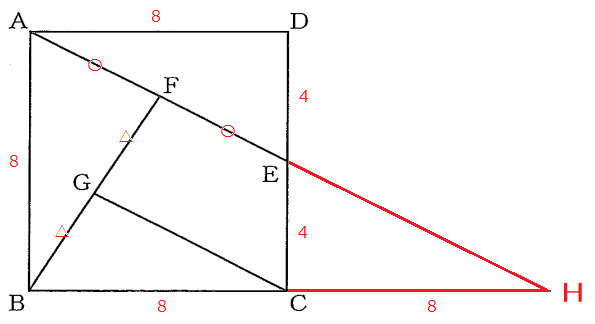
ここで分かっている長さを確認すると、
$\triangle$ADEについて、三平方の定理を使って、
AE=$\sqrt{8^{2}+4^{2}}=\sqrt{64+16}=\sqrt{16(4+1)}=4\sqrt{5}$
よって
HE=$4\sqrt{5}$
FはAEの中点だから
AF=FE=$\frac{1}{2}\times 4\sqrt{5}=2\sqrt{5}$
よって
FH=FE+HE=$2\sqrt{5}+4\sqrt{5}=6\sqrt{5}$以上から
$GC=\frac{1}{2}FH=\frac{1}{2}\times 6\sqrt{5}=3\sqrt{5}\ cm$
―――<解法2>―――
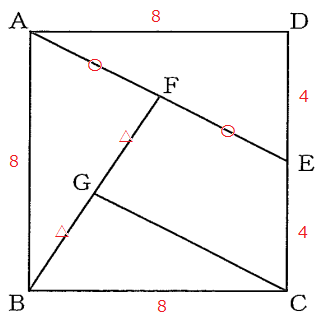
まず題意から分かる情報を書き込む。
斜めの線の長さと言えば三平方の定理であるが、求める線分GCを含む$\triangle$GBCは直角三角形かどうかわからない。
そこで補助線を引いて直角三角形をつくり出そうと考える。
また、この問題では「中点」がやたらと多いので「中点連結定理」が使えないかとも考える。
このような思案を経て次のような補助線を引く。
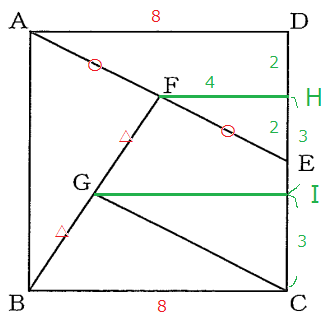
$\triangle$AEDに中点連結定理を用いれば、FH=AD×$\frac{1}{2}$=4であり、EH=HD=2である。
よってCH=8-2=6だから、CI=IH=3となる。CGを求めるために線分GIの長さが必要になる。それを知るために、さらに補助線を引く。
$\triangle$AEDに中点連結定理を用いれば、AJ=JD=4
よってBK=AJ=4
今度は$\triangle$FBKに中点連結定理を用いれば、
GL=BK×$\frac{1}{2}$=2
FH=LI=4だから
GI=2+4=6以上から$\triangle$GCIに三平方の定理を用いて、
$GC=\sqrt{6^{2}+3^{2}}$
$=\sqrt{45}$
$=3\sqrt{5}$
―――<解法3>―――
※ この解法3は「個別学習のセルモ 日進西小学校前教室」の西尾先生からご提供ただきました。ぜひ西尾先生のブログもご参照くださいませ。
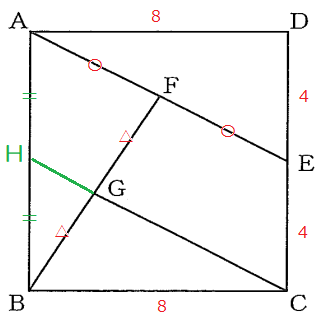
※ この解法がおそらく最短かつエレガントかもしれません。ただし厳密な証明には高校数学の「ベクトル」の知識が必要です。辺ABの中点をHとし、線分HGを書き込みます。
AH//EC、かつ、AH=EC、だから四角形AHCEは平行四辺形
よって
AE=HCもしもHGとGCが一直線上にあれば、
GC=HC-HG
で求まる。まず中点連結定理より
HG//AF
HG=$\frac{1}{2}AF$ …①
よって
HG//AE//HC
だからHGとGCは同一直線上にある(※)三平方の定理より
AE=$\sqrt{8^{2}+4^{2}}=4\sqrt{5}$
AEの中点がFだから
AF=$\frac{1}{2}AE=\frac{1}{2}\times 4\sqrt{5}=2\sqrt{5}$
①より
HG=$\frac{1}{2}AF=\frac{1}{2}\times 2\sqrt{5}=\sqrt{5}$
よって
GC=HC-HG=AE-HG
$=4\sqrt{5}-\sqrt{5}=3\sqrt{5}$(※)注意事項!
HGとGCが同じ直線上?
HG//AE//HC から HGとHCが同一直線上にあることが言えますが、厳密には、まだHGとGCが同じ直線上であるとは言えません。
しかし作図をすれば、どうやってもHGとGCが同じ直線上になるようにしか描けません。
ですから「AGCは一直線だ!」と分かったのが直感的だったとしても、解ければよいと思います。
式を使って厳密な証明をするには、高校2年生の「ベクトル」の知識が必要です。
②【中3】 四角形FGCEの面積は何$\ cm^2\ $か、求めなさい。
―――<① を解法1 で解いた場合>―――
四角形FGCEの面積=$\triangle$FBH-$\triangle$GBC-$\triangle$ECH
で求めることにする。
$\triangle$FBHの面積を求めるためには、その高さを求めたい。そこで次のように補助線を引く。
$\triangle$ABH∽$\triangle$FIH
である。また
$BI=8\div 2=4\ $
$IH=BH-BI=16-4=12$
であるから、相似比は
$16:12=4:3$
である。よって、
FI=$AB\times \frac{3}{4}=8\times \frac{3}{4}=6$以上から
$\triangle$FBH=$\frac{1}{2}\times BH\times FI=\frac{1}{2}\times 16\times 6=48$$\triangle$BCGと$\triangle$BHFの相似比は$\ 1:2\ $だから面積比は$\ 1:4\ $
よって
$\triangle$BCG=$\frac{1}{4}\times \triangle FBH=\frac{1}{4}\times 48=12$
また
$\triangle$ECH=$\frac{1}{2}\times 8\times 4=16$以上から
四角形FGCEの面積=$\triangle$FBH-$\triangle$GBC-$\triangle$ECH
$=48-12-16=20\ cm^{2}$
―――<① を解法2 で解いた場合>―――
四角形FGCEの面積=$\triangle$FGL+台形FLIE+$\triangle$GCI
$EI=HI-HE=3-2=1$
だから、
$=\frac{1}{2}\times 2\times 3+\frac{1}{2}\times (1+3)\times 4+\frac{1}{2}\times 6\times 3$
$=3+8+9$
$=20\ cm^{2}\ $
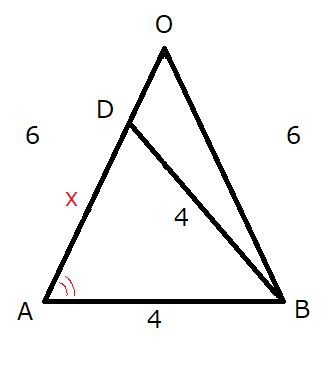
(3)【中1&中3】 図で、立体OABCは$\triangle$ABCを底面とする正三角すいであり、Dは辺OA上の点で、$\triangle$DBCは正三角形である。
OA=OB=OC=$6\ cm\ $、AB=$4\ cm\ $のとき、次の①、②の問に答えなさい。
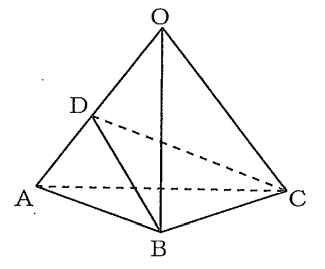
①【中3】 線分ADの長さは何$\ cm\ $か、求めなさい。
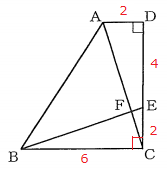
※ この解法は「個別学習のセルモ 日進西小学校前教室」の西尾先生からご提供ただきました。ぜひ西尾先生のブログもご参照くださいませ。
線分ADを含む$\triangle$OABについて考える。問題文で与えられた長さも書き込むと下図のようになる。
$\triangle$DBCは正三角形だから、AB=DB=4cmすると$\triangle$OABと$\triangle$BADが相似なのではないかと思えてくるので確かめる。
$\triangle$OABと$\triangle$BADについて、
$\triangle$OABは二等辺三角形であるから∠OAB=∠OBA
$\triangle$BADも二等辺三角形であるから∠BAD=∠BDA
また共通の角であるから∠OAB=∠BAD
よって2角がそれぞれ等しいので
$\triangle$OAB∽$\triangle$BAD以上から、
$OA:AB=BA:AD$
$6:4=4:x$
$6x=16$
$x=\frac{16}{6}$
$=\frac{8}{3}\ cm$
②【中3】 立体ODBCの体積は正三角すいOABCの体積の何倍か、求めなさい。
全問いから、
$OA:DA=6:\frac{8}{3}=18:8=9:4$
よって
三角すいOABCと三角すいDABCの高さの比も$\ 9:4\ $
両者は底面積が共通なので、体積の比も$\ 9:4\ $立体ODBCの体積=三角すいOABC-三角すいDABCだから、
三角すいOABCと立体DABCの体積の比は、$\ 9:(9-4)=9:5\ $以上から、立体DABCの体積は正三角すいOABCの
$5\div 9=\frac{5}{9}\ $倍
謝辞
解法と解説の作成にあたりましては、
- 日進市の「個別学習のセルモ 日進西小学校前教室」の西尾先生
- 大阪市住之江区の「あおい塾」の神田先生
にご協力いただきました。
おかげさまで図形問題の解説にあたっては、よりエレガントな解き方を用意することができました。
この場を借りて、あらためて御礼申し上げます。
あとがき
A日程にくらべると、大問3の図形問題が難化した印象です。
大問2は数学というよりも読解問題の様相が強いです。どの教科も全体的に論理国語の1点に集約していくような方向性は、あまり好ましくありません。
文字列だけで問題文を長くして難易度を上げようとする姿勢は、今後コンピューターを活用していく時代には向けては、あまり相応しいとは言えません。
より多様な情報提示のあり方で問題を作っていくべきというのが、今後の課題と言ったところでしょう。
もしも問題を作成する人たちが、コンピューターで読み書きできる情報が文字列しかない、というのであれば、それは能力上の問題です。
なぜ、こんなにもダラダラと長い問題文になってしまったのか、大いに反省すべきでしょう。
日本から国際競争力のある人材をどんどん輩出するのなら、早くこのボトルネックを解消すべきです。
進学実績
卒塾生(進路が確定するまで在籍していた生徒)が入学した学校の一覧です。
ちなみに合格実績だけであれば更に多岐・多数にわたりますが、当塾の理念に反するので生徒が入学しなかった学校名は公開しておりません。
国公立大学
名古屋大学、千葉大学、滋賀大学、愛知県立大学、鹿児島大学
私立大学
中央大学、南山大学、名城大学、中京大学、中部大学、愛知淑徳大学、椙山女学園大学、愛知大学、愛知学院大学、愛知東邦大学、同朋大学、帝京大学、藤田保健衛生大学、日本福祉大学
公立高校
菊里高校、名東高校、昭和高校、松陰高校、天白高校、名古屋西高校、熱田高校、緑高校、日進西高校、豊明高校、東郷高校、山田高校、鳴海高校、三好高校、惟信高校、日進高校、守山高校、愛知総合工科高校、愛知商業高校、名古屋商業高校、若宮商業高校、名古屋市工芸高校、桜台高校、名南工業高校
私立高校
中京大中京高校、愛工大名電高校、星城高校、東邦高校、桜花学園高校、東海学園高校、名経高蔵高校、栄徳高校、名古屋女子高校、中部第一高校、名古屋大谷高校、至学館高校、聖カピタニオ高校、享栄高校、菊華高校、黎明高校、愛知みずほ高校、豊田大谷高校、杜若高校、大同高校、愛産大工業高校、愛知工業高校、名古屋工業高校、黎明高校、岡崎城西高校、大垣日大高校
(番外編)学年1位または成績優秀者を輩出した高校
天白高校、日進西高校、愛工大名電高校、名古屋大谷高校
※ 成績優秀者・・・成績が学年トップクラスで、なおかつ卒業生代表などに選ばれた生徒
生徒・保護者様のお友達登録はこちら
LINE登録するとプレゼントがもらえます!
【会員限定】お子様の成績と可能性を伸ばす18個のノウハウ
塾関係者様のお友達登録はこちら
LINE登録するとプレゼントがもらえます!
「zoomで簡単。オンライン授業移行の教科書」
または個別対談も可
名古屋市天白区の植田で塾を探すなら個別指導のヒーローズ!!
★ 直接のお問い合わせ ★
――――――――――――――――――――――
個別指導ヒーローズ 植田一本松校
〒468-0009
名古屋市天白区元植田1-202 金光ビル2F
TEL:052-893-9759
教室の様子(360度カメラ) http://urx.blue/HCgL