塾長です。
気が付いたら何か月もブログを書いていませんでした。
ちょっと遅れましたが・・・
いやー忙しかった~
受験も、学年末テストも、新学期の準備も、全てひと段落しました。
今週から新しい指導システムを導入しましたが、その準備もひと段落しました。
合わせて、教室では一足早く新学年をスタートいたしました。
ご協力いただきました保護者様、生徒の皆様、講師の皆さん、ありがとうございます!
そんなわけで、ずっと内部の充実を優先して作業をしてきました。
おかげで新しい生徒の募集は全くしてませんでした。
やっと少し余裕が出て来ましたので、もしもお問い合わせはがあれば、ヒーローズ本部経由でお知らせくださいませ。
さて、少し遅れてましたが、卒業生の皆さんに言葉を贈りたいと思います。
卒業生へ贈る言葉 2023
ご卒業おめでとうございます。
あまり偉そうなことは言えませんが、塾長の少ない経験と知識から分かる限りの言葉を贈りたいと思います。
そこで今日のブログのタイトルの通り、
「偏差値でも学歴でもなく、どこでも楽しめる力」
ということを書きたいと思います。
人工知能は敵か味方か?
少し前、みなさんが志望校の校舎で、希望と緊張感をもって試験問題に挑んでいたころ、
世間ではChatGPTと呼ばれる人工知能が話題になっていました。
↓↓↓ これです ↓↓↓
Introducing ChatGPT
一言でいえば「何でも博士」です。質問すると何でも答えてくれます。
そんな人工知能の無料サービスです。
きっとご存じの方も多いでしょう。
色々なYouTuberたちが、ChatGPTの解説動画を上げていますので、細かい説明はそちらに譲ります。
ChatGPTが、なぜ大きな話題になったのでしょうか?
それは、人工知能の能力が、多くの人の予想をはるかに超えて優秀だったからです。
ある人はチャンスを感じましたし、またある人は不安を感じました。
みなさんも、ぜひ使ってみてください。
多かれ少なかれ、きっと価値観が変わることでしょう。
どんなものなのか、ちょっとお見せしますね。
ChatGPTの利用例
まず手始めに中学2年生の理科の単元「植物の体のつくりとはたらき」について質問してみました。
今年の愛知県校公立高校入試でも、大問2で出題されましたね。

上のように、すぐに答えが返ってきました。とても便利です。
(人工知能の答えが正しいとは限りません。そのつど確認が必要です。)
せっかくですから、新学期に関係することも聞いてみましょう。
例えば、文化祭の企画について相談してみたらどうでしょうか。
今週からマスク規制が緩んだことだし、こんな質問をしてみましょう。
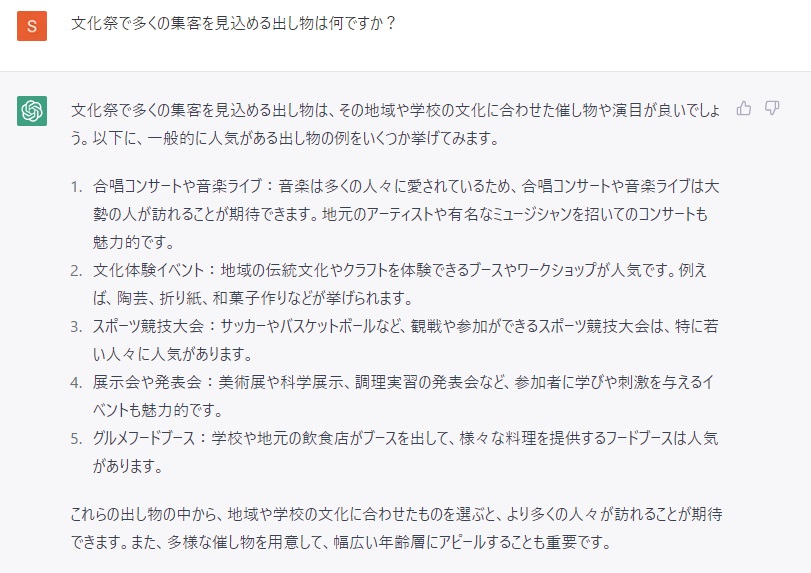
体育祭の企画も混じっちゃいましたが、参考になりますね。
さて、これをヒントにクラスで話し合いを進めた結果、上の1や4から着想を得て、演劇をすることになったとしましょう。
他のクラスと被らないよう、できればストーリー展開は完全オリジナルにしたいところです。
すると誰かが物語を作る必要があります。
「だれか物語を作れませんか?」
しかし誰も手を挙げません。どうしましょう?
まぁ、それも人工知能に考えてもらったらどうでしょう。

おお!
10秒も経たないうちに、演劇用の物語が作られてしまいました。
こちらからの質問の内容が、物語のメタ情報として混ざってしまったのは予想外。
でも、オチが無難だし、これはこれで良い演劇ができそうですね。
ということで、ChatGPT、すごくないですか?
ちなみに、数学の質問も答えてくれるし、簡単なプログラムなら作ってくれますよ。
ネット検索の上位互換なんてもんじゃありません。
まったく新しいコンピューターの使い方が登場してしまった、というのがお分かりいただけるでしょう。
みなさんなら、どんな使い方をしますか?
なぜ勉強するのか?
このような便利な人工知能が、これからどんどん出てきます。
しかも多くは無料で使えます。
すでに検索やLINEなど、いくつかのアプリの裏で人工知能が動いています。
きっと、みなさんが大人になる頃には、人工知能を抜きにして生活する方が難しいでしょう。
さて、人工知能が何でも答えてくれるなら、もう私たちは勉強しなくても良いのでしょうか?
作文の宿題は人工知能に作らせればよいのでしょうか?
そもそも宿題を出すことに意味があるのでしょうか?
みなさん、ここは真剣に考えてみるところだと思います。
ぜひ考えてみてください。
皆さんが学ぶ意味とは何でしょうか?
わざわざ努力して能力を身に着けるのは、何のためでしょうか?
高校や大学に進学してから、そこで何をどう学びますか?
こういうことを考えざるを得ない時代になってしまいました。
人工知能に負けない能力?
昔からコンピューターは大量の「データ」を処理するのが得意でした。
しかし一方で、「情報」は処理できないだろうと思われてきました。
数字の1つ1つが「データ」だとすれば、それらの意味もセットにした文脈が「情報」と言えるでしょう。
コンピューターは基本的に計算器ですから、数値を処理できても、それらの意味は理解できません。
つまり、コンピューターが処理できるのは「データ」までで、それを「情報」として処理するのは人間にしかできないだろう、ということです。
だから、
人間は情報の扱い方を鍛えればコンピューターに負けないはずだ!
ほんの10年くらい前までは、そんな風に言われてきました。
ところがここ数年で、どうやら「情報」も処理できるようになってしまったようです。
正確に言えば、今でも相変わらずコンピューターが何かの意味を理解することはないのでしょう。
けれども、あたかも理解して答えたかのような結果を生み出せるようになってしまいました。
少なくともコンピューターが意味の通る文章をすばやく作り出せる事実を、ChatGPTによって誰もが体験できます。
しかもその作文力は、その辺の大学1年生よりも優れたレベルと言えます。
だから人間がコンピューターよりも優秀だと言えることが、それだけ失われてしまったと言えます。
人工知能に職を奪われる・・・
という危機感をあおる人たちが増えて来ましたが、そう考えるのも自然でしょう。
人工知能が「情報を処理できない」という壁を突破してきました。
コンピューターができるのであれば、人間にとって、
知識の詰め込み教育なんて意味がない!
という流れになってきました。
教科書の裏側
実は、皆さんが学校で学んできた教科書にも「人工知能に負けない」という方針が反映されています。
学校の先生は、それらを意識して皆さんに授業を提供しています。
例えば、
- 人工知能は想像力がないから、人間は想像力を鍛えるべきだ。
- 人工知能は自発的に行動できないから、人間は主体性を強化すべきだ。
- 人工知能は図や表などの理解が苦手だから、人間は資料を読み解く能力を鍛えるべきだ。
といったような教育方針です。
これは分かりやすいし、納得しやすいでしょう。
皆さんが経験した高校受験や大学受験の出題傾向が、どんどん変わっているのはそのためです。
- 問題文の文章が長くなってきた
- 問題文の中でやたらと図表が増えてきた
という出題傾向の変化は、
「人工知能に負けない」
という方針が色濃く反映されているからです。
長文や図表の中から必要な情報を持ってきて編集し、回答としてまとめる・・・
そのような情報処理はコンピューターが苦手であるからこそ、人間の能力として伸ばすべきだ。
そして入試としてそのような出題をすれば、学校の教育も変わるはずだ。
そういう方針が色濃く出ています。
しかし、ChatGPTの能力が予想以上に高かったのがショックでした。
人工知能が苦手なものなんて、そのうちに無くなってしまうのではないか?
そのようなショックです。
無謀な挑戦
追い打ちをかけるようですが、ChatGPT はほんの1例にすぎません。
文章だけにとどまらず、音楽、映像、動画など、色々な分野で人工知能が瞬時にコンテンツをつくってくれるサービスがどんどん出てきています。
さらに泣きっ面にハチですが、3月にChatGPTがバージョンアップしました。
文章だけでなく、画像も扱えるようになりました。
最初のリリースからたったの3か月、日本でニュースになってから、たったの2か月で、もう次のリリースです。
進化のスピードに人間が(報道が)ついていけません。
一方、教科書の改訂は4年ごとです。
教育方針を大きく変えるような教育改革は10年くらいの歳月を費やしています。
そして残念ながら、その10年前に国が想定した「人工知能に負けない」という教育方針は、いきなり音を立てて崩れつつあります。
どんな教科書を使って能力を鍛えたところで、いつかは必ず人工知能に追い超されるからです。
そういう事実を突きつけられてしまったのです。
ここから次のようなことを学ぶ必要があります。
次の教育改革や教科書の改訂を待っても無意味。
誰かが方針を決めてくれるのを待っているのも無意味。
私たちは自らの頭で考えて、刻一刻と変化に対応しなければならない。
断っておきますが、この話は、あくまでも「プロダクトやコンテンツを生み出す能力」つまり「既存の産業において生産性を高める能力」の話です。
人工知能に職を奪われないために、どんな能力を身に着けるべきか、コンピューターが苦手なことを身に着けるべきだ、という文脈での話です。
もちろん、人工知能が感情や感性を獲得することに関しては、あいかわらず不可能だろうと、多くの人が考えています。
塾長もそう思います。
人間の成長を促し、暖かく見守るという学校教育が無くなることは今後もないでしょう。
話を戻しますが、
「プロダクトを生み出す能力」という意味では、もはや人間が人工知能に1つも勝てなくなる日が来るのは時間の問題と言えます。
そういう意味で「人工知能に負けない」という目的で勉強しても、それは理由にはならないでしょう。
人工知能に挑戦するために勉強するのはやめた方が良いと思います。
シンギュラリティ
このまま人工知能が賢くなっていって、ある日、とうとう人間の脳と同等の能力を手に入れてしまう日が来たとしましょう。
そのような日のことを「シンギュラリティ」と呼ぶそうです。
「技術的臨界点」とも呼ぶそうです。
要するに、シンギュラリティが人工知能の本当の誕生日というわけです。
ちなみに、人工知能が「感性」をも手に入れてしまうのは、さすがに無理だろうと思います。
というわけで、最初から感性を抜きにしてシンギュラリティの話をしています。
はた織り機の登場で、はた織り職人が仕事を失いました。
エクセルの登場で、暗算名人やそろばん名人を雇う必要がなくなりました。
こうして、職場から職人や事務員の仕事を、人工知能が次々に奪っていきました。
そしてある日、ついに人間は何1つコンピューターに勝てなくなりました。
あくまでもこのような文脈で「シンギュラリティ」が来るのは何年後でしょうか?
1年ほど前までは、2045年ころに訪れるだろうと予想されていました。
ところがここ半年の間に、その予想が更新されてしまったわけです。
今ではシンギュラリティの到来は2025年頃だろうと予想されています。
つまり、たったのあと数年です。
一気に20年も早まってしまいました。
競争以外で目的を見つけよう
ということで、何が言いたいかと言えば、
人工知能と競争しても、そんなの不毛なので止めましょう!
ということです。
コンピューターが便利になることは良いことです。
コンピューターに負けないとか、人工知能に負けないとか、そういう視野の狭いことを言っていても仕方がありません。
世の中をもっと便利にするために
世の中もっと良くするために
そういう前向きな目的を考えて、
そのために人工知能をどうやって活用するかを考えるべきでしょう。
やれ有休が欲しいだの、やれ残業が多いだの言っておきながら、
人工知能が仕事を代わりにやってくれるのを嘆くのはおかしなことです。
ちょっと冷静になった方が良いかなぁと塾長は思います。
世の中、いろいろなものが加速的に変化していますが、人工知能の話は、あくまでも1例にすぎません。
その1例に過ぎないものに、勝負を挑んで消耗してしまうのは時間の無駄です。
コンピューターは使うもの
人工知能も含めて、コンピューターは道具です。
正しい使い方を学ぶ。
それでよいのではないでしょうか。
大切なのは、コンピューターに追われたり、コンピューターに使われたりしないようにすることです。
これはお金に似ています。
お金の正しい使い方を学ぶことが大切です。
お金に追われたり、お金に使われたりしないことが大切です。
勉強も競争以外を目的にしましょう
人工知能との競争を止めるついでに、勉強で人と競争することも、止めてみたらよいと思います。
自分の点数を、友達と比較したり、親や兄弟と比較したりして、
優越感を覚えたり、劣等感を覚えたりすることがあります。
そういう気持ちの浮き沈みは、はっきり言ってしまうと、時間の無駄です。
気持ちが浮き沈みして落ち着いて勉強できなくなるくらいなら、
嫌な気持になったり、優越感で人の悪口を言うような性格になってしまうくらいなら、
最初から他人と比較しなければよいです。
そもそも偏差値は、他人との比較を抽象化するための数字です。
周りの人間と比較しなくても済むように、偏差値だけ見れば自分の実力の程度が客観的に理解できる、それでよいのです。
それを、わざわざ再びランキングに使ったり、他人と比較してしまったりしたら、話が循環するだけで前に進みません。
それで気持ちが浮き沈みするなんて、本当に意味がなくて、不毛な行為ですね。
しかも少子化で、間もなく高校も大学も、受験競争というものが無くなりますよ。
今年の愛知県の現状として、公立高校で4割、私立高校で6~7割が推薦で入学するようになっています。
おそらく今後も増えるでしょう。
もっといえば、公立高校の定員割れが止まりません。
愛知県の公立高校の定員割れは合計2000人以上で、もう毎年恒例です。
つまり、選ばなければ、もう名前を書くだけで合格します。
大学も同じ状況です。
さらに、勉強が苦手だとしても、コンピューターや人工知能を使えれば、何の問題もありません。
自分の弱点を克服できる手段や方法もまた、たくさんあるのです。
競争とは、数字を計算するルールを作り、その数字で優劣を決めるということです。
そして、数字を計算するルールを決めるときに、数字にならない多くのことを切り捨てます。
要するに、ルールを決められる程度に単純なものほど競争になる、ということです。
そして、そういった数字になりやすい競争ほど、だいたい人工知能に負ける運命にあるのです。
人間同士で競っていても、そんなのは視野が狭いというもの。
もっと大きな変化に飲み込まれる運命にあるのだということを、ちゃんと知っておくことが大切です。
逆に、受験で高揚しても後悔しても、それはごくごく狭い範囲での勝敗にすぎません。
すこし視野を広げれば、勝者もまた、人工知能に負ける運命にあります。
1回や2回の受験で幸先が明るくなるほど、世の中は甘くはないですし、また絶望なんてことも無いですよ。
幸せになったもん勝ち
このように、これから世の中がどんどん変化します。
それは個人の努力で止めることはできません。
ですから、変化を受け入れて、変化にうまく対応していくことが大切です。
その刻、一刻の対応の方が、実は受験よりもはるかに大切です。
競争の時代が終わり、人間が理解できない速さで環境が変化する世界になろうとしています。
競争するルールを決めても、もう次の瞬間には、そのルールが通用しなくなっている、そういう世界になります。
そんな世界の中で生きていくとき、いったい、何を目的にするのでしょうか?
他人と比較するのが無意味なのであれば、結局のところ、
自分にとっての幸せとは何か?
に行きつくのでしょう。
競争をした後で何とかするのではなく、競争の先にある目的を、最初から取りに行った方が早いです。
それは人それぞれに違います。
都会で精神を擦り減らせながら働いている人が、田舎の暮らしに憧れれたり、キャンプ場で不便な生活を楽しむことがあるように、
他人から見て、そんな生活は嫌だと思うような状態でも、また別の人から見たら、羨むような生活だと思われるのです。
親の世代が都会に移り住んできた時代には、田舎暮らしなんて嫌だと言って、みな都会に出て来たのでした。
何を良いと思うのかを判断する基準も価値観も、人それぞれに違います。
ちょっと昔までは、
「合格してから好きなことをやれ。それまでは我慢して勉強だけをやれ。」
「出世してから会社を変えろ。それまでは我慢して言うことを聞け。」
「定年退職後に好きなことをやるから、それまでは我慢して社畜で頑張れ。」
という人が多かったのですが、もうそんな前提はいっさい通用しません。
競争の結果を待つ必要なんてありません。
最初から幸せになるための目的を直接取りに行ってください。
母校を愛しなさい!
めでたく第一志望に合格した人
惜しくも第二志望へ進学した人
志望校を決める過程で、周りから妥協だの、背伸びだの言われた人
ものすごく勉強を頑張って満足した人
あまり努力しなくて、ちょっと後悔している人
人それぞれ、受験には色々な思いや事情や物語があっただろうと思います。
とにかく、そういう色々な過程を乗り越えて、みなさんは4月から進学します。
つまり、進学していく学校には、それだけ皆さんにご縁があったということです。
あとは、入学してから、みなさんが何をするかです。
どこへ進学したかではなく、進学先で何を成したのか。
第何志望に進学したかではなく、これからの生活をどれだけ楽しめるか。
みなさんの新生活の価値は、それで決まります。
良い成績を収めるかもしれませんし、そうでないかもしれません。
しかし、学校の成績は人生において、それほど価値はありません。
仕事をするようになってから学校の成績が問題になる確率は0%です。
ルールの範囲で学生の役割を果たすことは大切ですが、
それさえ守れば、あとは楽しんだもん勝ちだと思います。
人生と同じで、学校生活も、幸せを感じたもん勝ちです。
3年、4年も経てば、進学先の高校や大学を、また卒業することになります。
その時、自分の母校を誇れるかどうかは、みなさんが何をしたかで決まるのです。
だから、これから進学する学校のことを大好きになってください。
すてきな学生生活を、ぜひエンジョイして欲しいと思います。
卒業おめでとう。
みなさんの未来が幸せであることを切に願っております。
サムネイルの画像もAIが作成
今日のブログのサムネイル画像は、人工知能サービスの Stable Diffusion 2 で作成しました。
作成に使ったキーワードは下の7語で、作成時間は20秒ほどでした。
graduation high school happiness hope Japan anime
このブログだけのテーマソングも作ろうとしたのですが、私の知っていた作曲AIが有料化されてしまいました。
また無料の作曲AIが登場したら、作ってみようと思います。
進学実績
卒塾生(進路が確定するまで在籍していた生徒)が入学した学校の一覧です。
ちなみに合格実績だけであれば更に多岐・多数にわたります。生徒が入学しなかった学校名は公開しておりません。
国公立大学
名古屋大学、千葉大学、滋賀大学、愛知県立大学、鹿児島大学
私立大学
中央大学、南山大学、名城大学、中京大学、中部大学、愛知淑徳大学、椙山女学園大学、愛知大学、愛知学院大学、愛知東邦大学、同朋大学、帝京大学、藤田保健衛生大学、日本福祉大学
公立高校
菊里高校、名東高校、昭和高校、松陰高校、天白高校、名古屋西高校、熱田高校、緑高校、日進西高校、豊明高校、東郷高校、山田高校、鳴海高校、三好高校、惟信高校、日進高校、守山高校、愛知総合工科高校、愛知商業高校、名古屋商業高校、若宮商業高校、名古屋市工芸高校、桜台高校、名南工業高校、菰野高校(三重)
私立高校
愛知高校、中京大中京高校、愛工大名電高校、星城高校、東邦高校、桜花学園高校、東海学園高校、名経高蔵高校、栄徳高校、名古屋女子高校、中部第一高校、名古屋大谷高校、至学館高校、聖カピタニオ高校、享栄高校、菊華高校、黎明高校、愛知みずほ高校、豊田大谷高校、杜若高校、大同高校、愛産大工業高校、愛知工業高校、名古屋工業高校、黎明高校、岡崎城西高校、大垣日大高校
(番外編)学年1位または成績優秀者を輩出した高校
天白高校、日進西高校、愛工大名電高校、名古屋大谷高校
※ 成績優秀者・・・成績が学年トップクラスで、なおかつ卒業生代表などに選ばれた生徒
名古屋市天白区の植田で塾を探すなら個別指導のヒーローズ!!
★ 直接のお問い合わせ ★
――――――――――――――――――――――
個別指導ヒーローズ 植田一本松校
〒468-0009
名古屋市天白区元植田1-202 金光ビル2F
TEL:052-893-9759
教室の様子(360度カメラ) http://urx.blue/HCgL