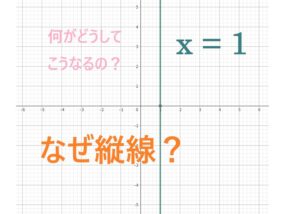塾長です。
少し前になりますが、とある中学2年生の保護者様から、数学のグラフについて相談を受けました。
おそらく、同じ疑問をお持ちの方も多いかと思います。
冬休みの宿題や冬期講習で復習すると思いますが、実は高校生でも分かってない場合が多いです。
納得できないグラフ
次のようなご相談でした。
中2の息子が「数学のグラフが分からない」と言っています。
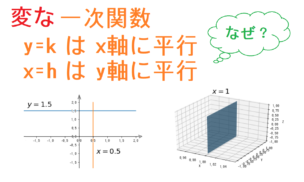
例えば、x=1 のグラフが描けません。
「縦一直線だよ」と教えても納得できないようです。
学校の先生に聞いても、塾の先生に聞いても、分からないそうです。
どうやって教えたらよいでしょうか?
なぜ?
どうして??
疑問に感じたことを納得するまで考える姿勢、とても大切です。
なかなか優秀ですね!
そこで、
「なぜ x=1 が縦線になるのか?」
について説明します。
まずは「イメージ」から入ります。直観力(センス)を養うことも大切です。
xではなく、xとy
数学のグラフを考えるとき、最初に確認することは何でしょう?
実は無意識のうちに選択しているのが「軸の本数」です。
「数直線の本数」と言い換えてもOKです。
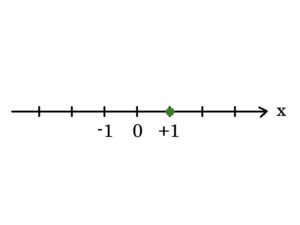
まず、変数がxだけの場合、つまりx軸だけの場合を考えましょう。
これは1本の数直線と同じです。
よって「x=1」のグラフは以下のような緑の「点」になります。
このx軸の数直線の中には、数が隙間なく並んでいます。
+1の横には+1.1がありますが、それらの間にも +1.01 や +1.0098 などが無数に存在しています。
その中で+1だけが選択されている、という状態を描いたのが上のグラフです。
この数直線の上下には何もありません。
細い一本橋の様なもので、左右には進めますが、上下に足を踏み外せば奈落の底です。
ただし、橋と違うのは「硬さ」という概念がありません。数が並んでいるだけですからね。
つまり、x軸の数直線は、どこまでも伸ばせると考えてOKです。
左右だけでなく、上下にも伸びるのがポイントです。
さて、中1の比例や反比例、中2の1次関数などでは、xとyの2文字を使います。
つまりx軸とy軸の2本のグラフになるわけです。
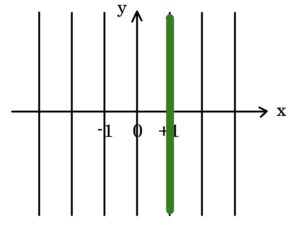
そこで上のグラフでy軸をニョキニョキっと生やしましょう。
上のグラフでは、まだx軸の上下が未使用でした。
x軸の上下には、まだ数を並べる余白が空いていますから、y軸を上下に生やします。
そこでx軸を上下にビヨーンと引っ張って伸ばします。
すると以下のようになるでしょう。
x軸の目盛りの罫線も一緒に引き伸ばされるイメージです。
ここでy軸の目盛りの罫線をどうするか考えましょう。
先にy軸を描いて、その横にx軸を生やした場合は次のようになりますから、
y軸の罫線は横に引き伸ばされるというイメージです。
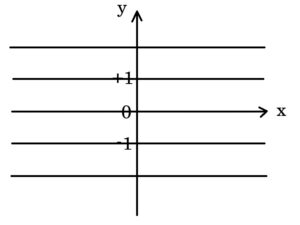
x軸とy軸のどちらが偉いということはないので、どちらの罫線も採用します。
よって方眼紙のような罫線になります。
こうして「x=1」は以下のようなグラフになるわけです。
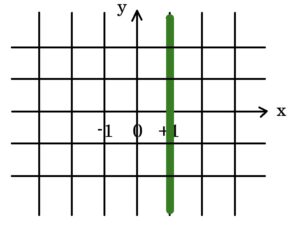
清書するとこうなります。
ちなみに、3つ目のz軸も追加するとどうなるでしょうか?
左右がx軸、上下がy軸ですから、前後をz軸にしましょう。
上のグラフを前後に伸ばしてz軸を生やすと、次のようになります。
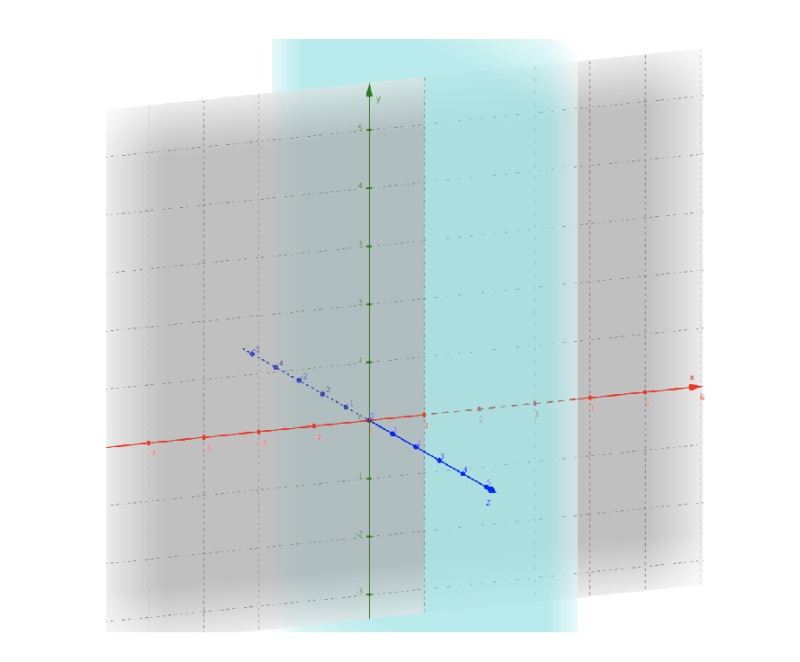
x=1は上の水色の平面です。
つまり立体のグラフでは、x=1は平面になります。
だいたい直感的にはこんなイメージです。
しかし、ちゃんとした説明にはなっていないため、もうすこし説明を続けます。
グラフは点の集まり
中学1年生の数学で、比例や反比例を学ぶ前に「関数の定義」を教わったはずです。
「yがxの関数」であるとは、
「xの値を決めると、それに対応してyの値がただ1つに決まる関係」のことである。
何よりもまず、こうした定義をしっかり覚えることが大切です。
成績が伸び悩む生徒は、こうした教科書の基本を覚えず、問題集だけをひたすら解いているケースが多いです。
実際、関数のグラフは関数の定義に沿って描かれるのです。
いくつか例を挙げて描いてみましょう。
y=3xのグラフ
比例の式 y=3x を例に、関数の定義にそってグラフを描いてみましょう。
つまり、次の手順でグラフを描いていきます。
- xの値を何か1つ決めると、それに応じてyの値も1つ決まる。
- そのx、yの値を座標の点としてグラフに描く。
- 1に戻って繰り返す。
上の手順は難解でも繰り返すことができます。
試しに、xを0.25ずつ変えて、何個か (x, y) の座標を求めて描いてみましょう。
| x | -2 | -1.75 | -1.5 | -1.25 | -1 | -0.75 | -0.5 | -0.25 | 0 | 0.25 | 0.5 | 0.75 | 1 | 1.25 | 1.5 | 1.75 | 2 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| y | -6 | -5.25 | -4.5 | -3.75 | -3 | -2.25 | -1.5 | -0.75 | 0 | 0.75 | 1.5 | 2.25 | 3 | 3.75 | 4.5 | 5.25 | 6 |
これをグラフ上に描くと、下図の点列部分のようになります。
さらに無限に繰り返すことができますから、グラフ上に描かれる点も無限に増えていきます。
やがて点と点がつながって、下図の赤い直線のグラフになっていきます。
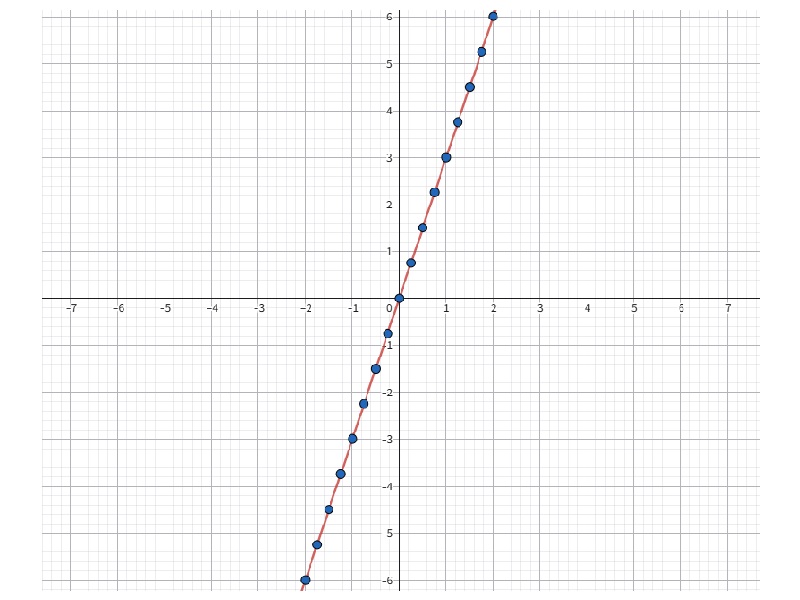
つまり「グラフは点の集まり」ということです。
y=1のグラフ
同様に考えて、今度は関数 y=1 のグラフを描いてみましょう。
xの値を何か1つ決めても、yの値は常に1ですから、以下のようになります。
| x | -2 | -1.75 | -1.5 | -1.25 | -1 | -0.75 | -0.5 | -0.25 | 0 | 0.25 | 0.5 | 0.75 | 1 | 1.25 | 1.5 | 1.75 | 2 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| y | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
この表をもっと細かくしていけば、やがてグラフは下図のようになります。
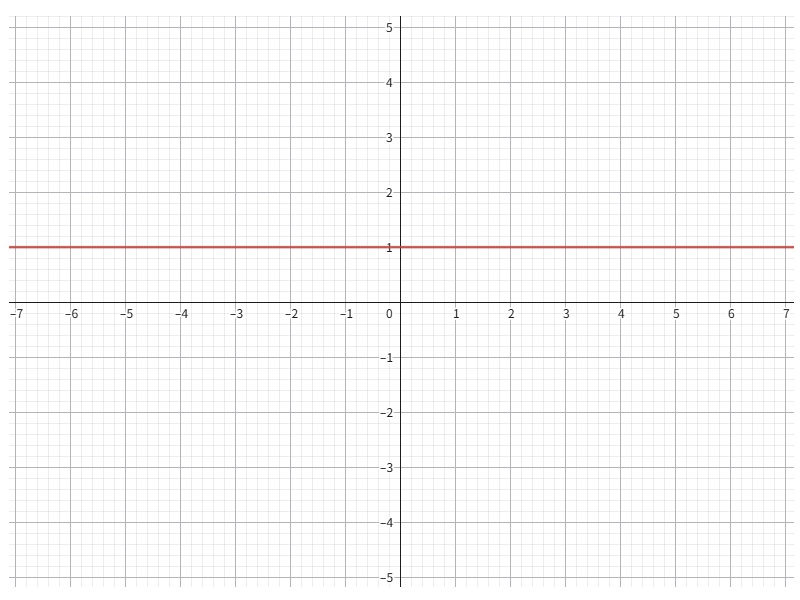
x=1のグラフ・・・
さて、いよいよ x=1 のグラフを考えたいのですが・・・できません!
x=1ですから、xの値は1としか決められません。
しかも、対応するyの値が不明です。
x=1という式には、yをどうするか書かれていません。
| x | 1 |
|---|---|
| y | ? |
つまり、x=1 は「yはxの関数」ではないのです。
これではグラフが描けません。
困りました。
どうしましょう・・・
関数ではなく方程式
ここで教科書に戻りましょう。
x=1 や y=1 のグラフは中学2年生で習います。
中学2年生の教科書を開いて、その単元のタイトルをあらためて確認してみると・・・
方程式とグラフ
「二元一次方程式 $ax+by=c$ のグラフについて考えましょう。」
とあります!
おや?
関数ではありません。
方程式です。
- 関数のグラフ
- 方程式のグラフ
という2つの言葉が出てきましたが、x=1のグラフは「方程式のグラフ」として習うのでした。
いつのまにか話が変わっていました。
教科書のタイトル、めちゃ大事です。
ここで、x=1は
二元一次方程式 $ax+by=c $ $ (a=1, b=0, c=1)$
すなわち
$x+0y=1$
と見ています。つまり、
$x, y$ の二元一次方程式 $x+0y=1$ の解をグラフに描きましょう。
という話に変わったのでした。
二元一次方程式は、xの値1つとyの値1つの組(座標)が1つの解となります。
つまり、
- x=1 という式には文字yも隠れている
- xとyの値の両方をワンセットで同時に考えるべき
ということです。
そこで、$x+0y=1$ を満たす $x, y$ の値の組み合わせを考えましょう。
yの係数はゼロですから、yに何を代入してもyの項は0になります。
つまり解 (x, y) は次のように、
$ \dots, (1, -5), (1, -4), (1, -3), (1, -2), (1, -1), (1, 0), (1, 1), (1, 2), (1, 3), (1, 4), (1, 5), \dots$
などなど、何個でも考えられます。
解がいくらでもあるわけです。
もちろんyの値は小数でも分数でもかまいません。
たとえば2つの解 (1, 0), (1, 1) を考えたら、その間にも無数の解があるわけです。
それらをグラフの座標として点を打っていきましょう。
無数の点をグラフに描いていくことを想像してみてください。
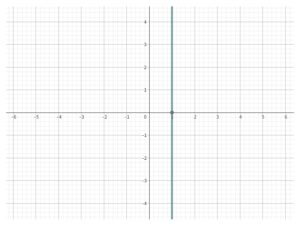
それらの点と点がつながり、やがて縦の直線になることが分かるでしょう。
こうして、x=1のグラフは縦の直線として描かれるわけです。

ここまでの話をまとめると、
「yはxの関数」という世界では、x=1のグラフは描けません。
「yとxの二元一次方程式の解」という世界なら、x=1のグラフを描けます。
ということです。
関数のグラフが分からない!
というお子様の感覚は、実は正解なのでした。
暗黙のルールをあぶり出そう!
これまでの話を整理して、数学のセンスみたいなもの引き出しましょう。
あらためて最初の問題を振り返ってみます。
x=1のグラフを描け。
(回答欄はx軸とy軸の描かれた方眼用紙)
ここで、
x=1のグラフを描け。
という1行だけに着目してしまうと、次のようなグラフを描いてしまうでしょう。

y軸を使っていないため、これは間違いとして採点されます。
回答欄はx軸とy軸の両方がある方眼紙です。
つまり、この問題には
変数xと変数yを同時に満たすことを前提として
というルールが暗黙のうちに設定されている、と見なすべきです。
そして「関数」とは言われていません。
そもそも「yはxの関数」と解釈したらグラフが描けないわけです。
だから、
$x, y$ の二元一次方程式 $x+0y=1$ の解をグラフに描きましょう。
という解釈をしてグラフを描き、次のようになったのでした。

ここで次の2行は同じです。
$x, y$ の二元一次方程式 $x+0y=1$ の解をグラフに描きましょう。
$x, y$ の二元一次方程式 $x=1$ をグラフに描きましょう。
この2行を見比べると、つぎの暗黙のルールが言えるでしょう。
条件の指定がない変数には、どんな数をあてはめても良い。
いかがでしょうか?
考え方をまとめます。
x軸とy軸の2つの軸がある世界においては、変数xの値に対する変数yの値も、常にセットで考えます。
その上で、変数xに対してはx=1と指定されていますが、変数yに対しては何も指定されてません。
これを「変数yの係数が0である」と解釈したので、
「yの値は何でもよい。」
「yは全ての実数をあてはめてOK!」
という考えになりました。
これを短く言えば、
yについて条件の指定が書かれていないので、yの値は何でもよい!
と見なせるわけです。すなわち、
x-y 平面のグラフにおいて、
「$x=1$」は「$x=1$ かつ $y=何でもOK$」と同じ
と解釈しましょう。
そうすれば次のように、いくらでも解を書き出せます。
$ \dots, (1, -5), (1, -4), (1, -3), (1, -2), (1, -1), (1, 0), (1, 1), (1, 2), (1, 3), (1, 4), (1, 5), \dots$
あとは上で見たように、これらをグラフにしていけば、やがて縦一直線のグラフになります。
このように
数学では条件の指定がない変数には、どんな数をあてはめてもよい
と解釈します。
これが、暗黙のルールみたいなものです。
話が飛躍しているでしょうか?
いえ、そんなことはありません。
ちゃんと別の説明もできます。
高校1年生の「集合と命題」でも表現できます。
命題の単元では「反例が見つからなければ真(正しい)」を学びますが、これを使います。
集合で表すと { $x, y | x=1, y \in R $ } です。
この集合において、
$y=5$ としても、$x=1$ は成り立つ( $x=1$ が成り立たなくなる場合が見当たらない)。
$y=-100$ としても、$x=1$ は成り立つ( $x=1$ が成り立たなくなる場合が見当たらない)。
・・・
つまり、yはどんな実数でもOK!
こんなふうに考えるわけです。
逆に、中学生までの間に「方程式のグラフ」を十分に経験しておかなければ、集合を実数まで拡張することが難しいでしょう。
まとめ
- グラフの軸の本数(変数の数)を確認する
- x軸とy軸を使うx-y平面のグラフでは、常にxとyを同時に考える(座標で考える)
- x-y平面のグラフにおいて、xの条件が指定されていない時は「xはどんな数でも良い」と考える
- x-y平面のグラフにおいて、yの条件が指定されていない時は「yはどんな数でも良い」と考える
- x軸とy軸とz軸を使う立体のグラフでは、常にxとyとzを同時に考える(座標で考える)
- 以下、文字を増やしても同様・・・
以上から
- 軸が1つだけ(x軸だけ)の世界では、x=1は数直線上の1点になる
- 軸が2つ(x軸とy軸)の世界では、x=1は平面上の直線になる(x=1、y=全ての数)
- 軸が3つ(x軸とy軸とz軸)の世界では、x=1は立体空間の中の平面になる(x=1、y=全ての数、z=全ての数)
教科書には全て書くべき?
今回は中学2年生がグラフの読み書きでお悩み、という件で考えてきました。
悩む根本的な理由は「教科書が読みにくいから」だろうと思います。
なぜ読みにくいかというと、上で見て来たように、数学には独特の読み方や解釈があり、それがなかなか掴めないからです。
タイトルや回答形式まで気にしながら式を読まなければならないのは辛すぎますよね。
「x=1のグラフを描け」
とは
「x-y 平面において $x+0y=1$ のグラフを描け」
という意味でした。
「変数yも同時に考えなさい」
という大前提が隠れていたのでした。
だったら、最初からそうに書けばいいじゃん!
などと文句の1つでも言ってやりたくなるでしょう。
5教科の中で最も行間を読まなければならないのが数学かもしれません。
学校では先生が、この行間を説明しながら授業を進めます。
ちゃんと行間を説明できる先生が、分かりやすい先生、ということになるでしょう。
数学は、式によって簡潔かつ厳密にものごとを表現できる、というのが最大の特徴です。
数式の意味を日本語で説明すると長くなったり、ときに説明が不可能だったりします。
そういうメリットがある反面、読み方の訓練が必要です。
これはプログラミング言語でも同じですね。
そして数学の記述も完ぺきではありません。
例えば、よく言われているのが、カンマ記号を「かつ」と読むべきか「または」と読むべきか論争です。
「かつ」と「または」は論理的に逆の意味ですが、その相反する意味が1つの文字に与えられているのですから、ややこしいです。
例えば、
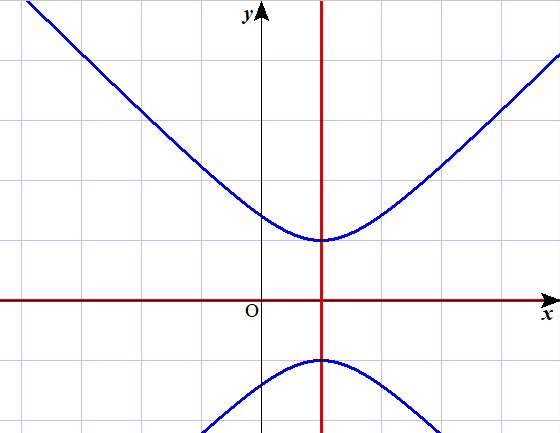
二次方程式 $ x^2=1 $ の解は $ x=1,-1 $ ですが、この時のカンマは「または」です。
一方、
連立方程式 $ 2x+y=7, 5x-y=14$ の解は $(3, 1)$ ですが、これらのカンマはどれも「かつ」です。
このように場面によってカンマを読み分けるよう、知らないうちに訓練されているわけです。
同じカンマという文字に、2つの意味、しかも真逆の意味があるので、言語のつくりとしては欠陥(仕様バグ)と言えます。
ですから教科書には、その読み方について注意書きを載せるべきだと塾長は思います。
さて、現代は不登校が普通になってきました。
それどころか年齢に関係なく、独学で何かを学んだり、あるいは学び直したりすることが頻繁になっています。
超高齢社会で人生が長くなり「リラ―ン」の重要性が高まっていますから、なおさらでしょう。
その中で、中学校や高校の数学を独学する人も増えていくと思います。
そこには行間を説明してくれる先生はいません。
このような時代において、教科書には、もっと行間の説明を分かりやすく載せておく必要があるのかもしれませんね。
進学実績
卒塾生(進路が確定するまで在籍していた生徒)が入学した学校の一覧です。
ちなみに合格実績だけであれば更に多岐・多数にわたります。生徒が入学しなかった学校名は公開しておりません。
国公立大学
名古屋大学、千葉大学、滋賀大学、愛知県立大学、鹿児島大学
私立大学
中央大学、南山大学、名城大学、中京大学、中部大学、愛知淑徳大学、椙山女学園大学、愛知大学、愛知学院大学、愛知東邦大学、愛知工業大学、同朋大学、帝京大学、藤田保健衛生大学、日本福祉大学
公立高校
菊里高校、名東高校、昭和高校、松陰高校、天白高校、愛知教育大学附属高校、名古屋西高校、熱田高校、緑高校、日進西高校、豊明高校、東郷高校、山田高校、鳴海高校、三好高校、惟信高校、日進高校、守山高校、愛知総合工科高校、愛知商業高校、名古屋商業高校、若宮商業高校、名古屋市工芸高校、桜台高校、名南工業高校、菰野高校(三重)
私立高校
愛知高校、中京大中京高校、愛工大名電高校、星城高校、東邦高校、桜花学園高校、東海学園高校、名経高蔵高校、栄徳高校、名古屋女子高校、中部第一高校、名古屋大谷高校、至学館高校、聖カピタニオ高校、享栄高校、菊華高校、黎明高校、愛知みずほ高校、豊田大谷高校、杜若高校、大同高校、愛産大工業高校、愛知工業高校、名古屋工業高校、黎明高校、岡崎城西高校、大垣日大高校
(番外編)学年1位または成績優秀者を輩出した高校
天白高校、日進西高校、愛工大名電高校、名古屋大谷高校
※ 成績優秀者・・・成績が学年トップクラスで、なおかつ卒業生代表などに選ばれた生徒
名古屋市天白区の植田で塾を探すなら個別指導のヒーローズ!!
★ 直接のお問い合わせ ★
――――――――――――――――――――――
個別指導ヒーローズ 植田一本松校
〒468-0009
名古屋市天白区元植田1-202 金光ビル2F
TEL:052-893-9759
教室の様子(360度カメラ) http://urx.blue/HCgL