ゼロ除算

塾長です。

たまに虚構新聞の記事を見て爆笑しています。
ある虚構新聞のファンから次のアドバイスをいただきました。

科学面の「『２と１は等しい』数学界で論議」という記事が面白いよ。これ教育に使えるんじゃない？

2008年の記事です。
こんな素晴らしい記事を見過ごしていたとは。

１＝２の証明！！　ホント？ウソ？

まず問題となっている「１＝２」の証明を見てみましょう。

問題となった証明

上の記事からの抜粋と補足です。中３以上の知識で読めるでしょう。

因数分解を使いますが、数学の好きな生徒ならば、中学２年生でも何とか読むことはできるでしょう。

$$a=b$$
両辺に $a$ をかけて
$$a^2=ab$$
両辺から $b^2$ を引いて
$$a^2-b^2=ab-b^2$$
両辺を因数分解して
$$(a+b)(a-b)=b(a-b)$$
両辺を $(a-b)$ で割って
$$a+b=b$$
ここで $a=b$ であったから
$$2b=b$$
両辺を $b$ で割って
$$2=1$$

むむむぅ・・・確かに結論が「２＝１」となってしまいました。

どうでしょう？

大真面目な質問

この証明は正しいと思いますか？

数学では、たった１つでも反例を言えれば間違いと言えます。
逆に言えば、何も間違えを指摘できなければ「正しい」ことになってしまいます。

もしも上の証明の間違いを言えなければ、みなさん、大変ですよ。

１＝２が正しいとなれば、また小学校から勉強のやり直しです。

それは嫌です。

何とかして証明の間違いを見つけたいところです。

いかがでしょう？

証明のどこが間違いなのか、みなさんは分かりますか？

どうしてこうなった？

計算のルール。たくさんあります。

その１つでも無視して計算してしまうと、このような詭弁が生まれてしまいます。

もちろん冗談としては、なかなか面白い証明です。

やってはいけないルール

それはさておき、

上の証明で無視したルールが１つあります。

それは何でしょうか？

このルールを無視してしまうと「何でもあり」の結論を好きなだけ導くことができます。

そのルールとは、

０で割ってはいけない

です。
このルールに違反してしまった計算のことを、

ゼロ除算

と呼びます。まるで犯罪名のような名前までついています。

教科書で明記されているか？

ゼロ除算

これについて、いつ学校で教わるのでしょうか？

割り算は小学３年生で習います。
しかし小学校では「指導しなくてよい」というスタンスです。
ただし一部の教科書では、国語的な意味で「答えは０」と解釈できる場合を紹介しています。

中学の教科書でも「０で割ることは考えない」としています。
これも、あまり明確に「０で割らないように注意しろよ！」と教えることはないようです。

このルールを明確に意識するのは、高校数学からです。
ゼロ除算を特別に取り上げるページは無いものの、式の証明や場合分けの過程で何度となく教わります。

どこでゼロ除算をしてしまったのか？

さて、話しを戻しましょう。

冒頭の証明のどこでゼロ除算を犯してしまったのでしょうか。

これは証明の式に、具体的な数字を当てはめれば分かりやすいでしょう。
特に次の式以降に着目です。

証明の中で、次の行に注目です。
$$(a+b)(a-b)=b(a-b)$$
ここで $(a-b)=0$ ですから、この式は、
$$(a+b)\times 0=b\times 0$$
ということです。
ここで両辺を $(a-b)$ で割る、つまり $0$ で割ってしまいました。

このように、０で割ってしまうルール違反をしていました。

なぜ０で割ってはいけないの？

それでは、そもそも０で割ってはいけない理由、なぜでしょうか？

破壊的だから

数学者の厳密な説明はさておき、まずは良くないことが起こる様子を経験しましょう。
上の式で見たようなことを、具体的な数字に置き換えてみれば分かりやすいです。

$$(a+b)\times 0=b\times 0$$
この部分をさらに
$$100\times 0=5\times 0$$
などと書いてみましょう。
これは右辺も左辺も確かに $0$ となって正しいです。
しかし両辺を $0$ で割ったらどうでしょう。
$$100=5$$
とたんに話がおかしくなります。

このように

「０で割る」

を許してしまうと、33=101 のような詭弁をいくらでも作れてしまいます。
０で割ることに

「意味が定まらない」

ので、それを逆手に取って

「どのような意味にも設定できてしまう」

とできてしまうからです。
これは、かなり破壊的です。
一般に、

$$x\times 0=y\times 0$$
を満たすような $x,y$ は「何でもよい（不定）」

です。
よって

「０で割る」

を許してしまうと、上で見たように

何でも＝何でも

という関係をいくらでも作れてしまい、おかしくなります。
数の世界が破壊されてしまいます。

よって、０で割ることを安易に許してはいけません。

そういうルールです！

意味が分からないから

そもそも「０で割る」とは、どういうことでしょうか？

例えば

$100÷5$

は、

「１００を５等分にした内の１つ」
または
「１００の中に５がいくつ入るか」

などという意味になります。
試しに後者の意味だとします。

では、

$100÷0$

の計算は、どうなるのでしょうか。

「１００の中に０はいくつ入るか？」

なぞなぞなら「２つ」というトンチも許されますが、割り算の答えにはなっていません。
かと言って、答えが分かりません。

「そもそも０の何個分？」

という意味が分かりません。
０は何個集めても０だからです。

計算が終わらないから

そこで１００歩譲って、

$100÷5$

から出発して、「割る数」の５を、どんどん小さくして０に近づけようと思います。

$100÷5=20$
$100÷0.5=200$
$100÷00.5=2000$
・・・
$100÷0.00000000\dots 005=2000000000\dots 00$

このように、割る数を０に近づければ近づけるほど、答えは無限に大きくなってしまいます。
これを繰り返していけば、いつか「０の何個分」か答えらえれそうです・・・

・・・しかし、割る数はどこまでも小さくできます。
出てくる答えも、どこまでも大きなります。

この作業は、いくらでも続けられます。
終わりません。
永遠に続きます。

結論が出ないから禁止

そして、いくら続けても、

「０で割る」

の結論が出ません。

宇宙が終わる頃には結論が出るのでしょうか？

それも分かりません。

さらに、良くないことがあります。
割られる数が１００であろうと１であろうと、２であろうと、とにかく

「答えが無限に大きくなり続ける」

ことに変わりがありません。
だからといって、

１００÷０
と
３÷０
が
無限の先で同じ答えになっているのか、あるいは違う答えになっているのか、それも分かりません。

このように「０で割る」という計算は、いくら考えても答えを特定できませんでした。
だから「０で割る」という計算の定義ができないことになります。

「０で割る」

とは

「わからない」

または

「永遠に計算が終わらない」

または

「そもそも計算の定義ができない」

ということになるわけです。

だから、

「０で割るな！」

となったわけです。

プログラミングでも禁止

プログラミングの世界、もっと言えば、コンピューターを使う世界でも、

「０で割ってはいけない！」

というルールが徹底されています。
プログラマーならだれでも

ゼロ除算

という悪魔を知っています。
これが出てきてしまうプログラムを書いてはいけません。

さて、実際にやったらどうなるのでしょうか？

試しに、Pythonというプログラミング環境で

$5÷0$

を計算した結果が次の画面です。

ちなみにプログラミングでは「５÷０」のことを「5/0」と書きます。

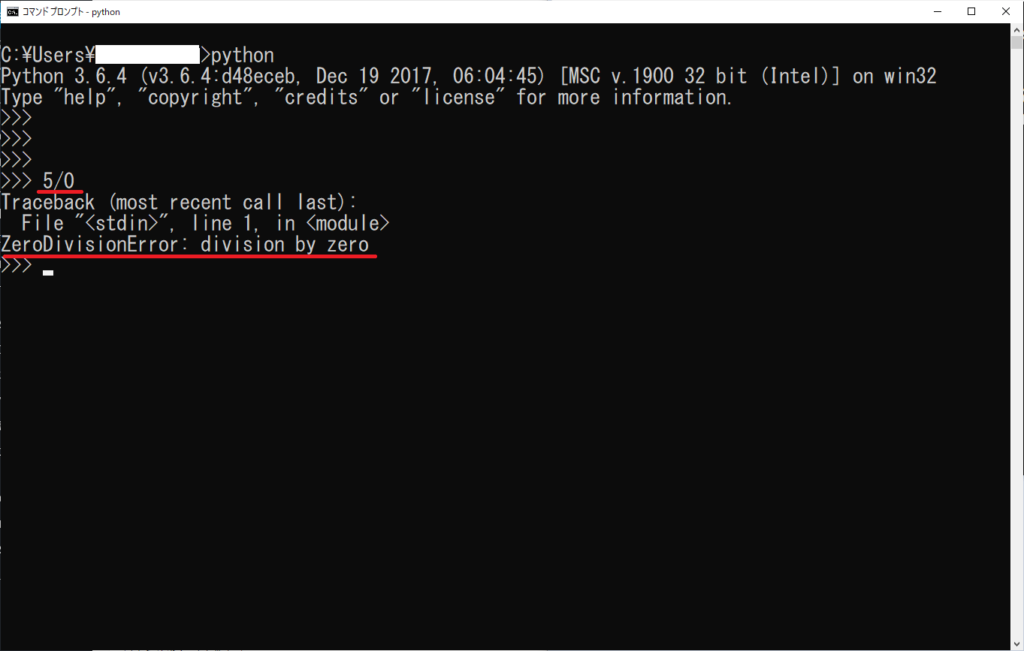
パイソンで０除算エラー

“ZeroDivisionError: division by zero”　（０で割ったというエラー）

というエラーが表示されて、怒られてしまいました。

近代的なプログラミング環境では、コンピューターに「÷０」を計算させる前に、その式を検出してエラーを出すようになっています。
コンピューター全体が止まってしまったら大変ですからね。

このようにコンピューターの世界でも「０で割る」は禁止です。
ですからプログラマーの世界では「ゼロ除算」と言ったら、それはバグ(*)の１つを指します。

これが本当に計算されてしまうと、最悪の場合、コンピューターが止まってしまいます。

(*) プログラムの不具合のこと

勉強したことを笑いに活かす

今回は虚構新聞の昔の記事から数学のお話をしました。

虚構新聞はフェイクニュースのサイトです。
このようにウィットの利いた面白いニュースをでっち上げるジョークサイトです。

文字通り「虚構」の新聞ですね。
このような分野では有名で、すでに不動の地位とも言えます。

本当のことを知っている人だけが楽しめます。

勉強したことをジョークに活用する。

そんな勉強の応用もあるんですね。
虚構新聞の記者たちの仕事は楽しそうです。

何に価値があるのか、何が仕事になるのか。

やってみないと分からないものです。

キャリア教育のネタにもどうぞ。

ゼロで割ったら答えが０？

最後に少し補足です。

特定の文脈において「０で割った」ときの答えを定義することは可能です。
例えば、

300gのケーキを100gずつ分けました。何人に配れるでしょう？

という文脈があったとします。この計算は、

$300÷100=3$

ですから、答えは

３人

となります。
つまり、この文脈では「割り算の答え」は「配れる人数」を意味します。
この文脈を前提として、

300gのケーキを0gずつ分けました。何人に配れるでしょう？

を考える場合はどうでしょう。同じように計算式は、

$300÷0=?$

となりますね。
もちろん式だけ見れば計算に困りますが、文脈から答えを決めることはできます。

答えが分からない → 配れる人が決まらない → 配れない → 配れる人数は０人

このように社会的な意味から答えを導いて、それに合わせて

$300÷0=0$

と無理やり決めてしまうことができます。
こうして、この文脈の中では、

「０で割った答えは０人」

と決めることができるでしょう。

実際、小学３年生の一部の教科書では、このような考え方を紹介しているコラムがあります。
ただし、あくまでも考え方の１つにすぎません。
こうした教科書の影響かどうか分かりませんが、中には、

「０で割ったら０だよ。」

と覚えてしまっている人もいます。
もちろん、これは早とちりです。
常には成り立たないからです。

これはあくまでも、上のような文脈だけに通用する決め方です。
数式に対して常に言えるものではありません。
つまり、

「ローカルルール」
にすぎません。

このように、０で割ったときの答えを決めるのは「特定の文脈上の都合」です。

それは数学というよりは、国語や社会、あるいは工学のお話しになります。

生徒・保護者様のお友達登録はこちら

LINE登録するとプレゼントがもらえます！
【会員限定】お子様の成績と可能性を伸ばす１８個のノウハウ

塾関係者様のお友達登録はこちら

LINE登録するとプレゼントがもらえます！
「zoomで簡単。オンライン授業移行の教科書」
または個別対談も可

名古屋市天白区の植田で塾を探すなら個別指導のヒーローズ！！

★ 直接のお問い合わせ ★
――――――――――――――――――――――
個別指導ヒーローズ　植田一本松校
〒４６８－０００９
名古屋市天白区元植田１－２０２　金光ビル２Ｆ
ＴＥＬ：０５２－８９３－９７５９
教室の様子（360度カメラ）　http://urx.blue/HCgL