塾長です。
もうすぐ、5月20日前後から1学期の中間テストですね。
ヒーローズ植田一本松校では、GW連休明けから「テスト対策プリント」をドサっと配ります。
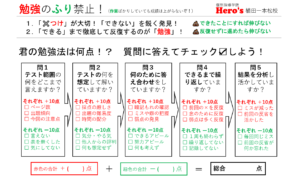
しかも「勉強法」がプリントされたクリアファイルに入れてプレゼントします!
ただ、そのプリントをやる前に、やることがありますよ。
今、テスト勉強は何をしていますか?
進級して最初のテストということで、今回はテスト勉強の「あたり前」を書きます。
テスト前の勉強「基本のキ」
勉強の仕方とは・・・当たり前の人には当たり前の方法。
しかし、そうでない人には「え、意外」「ぜんぜんやってない」といもの。
それくらい違うものです。
以下に基本事項を書きます。
「ヤベー」とおもったら、こそっと、なおかつ、今すぐに取り入れてみてください。
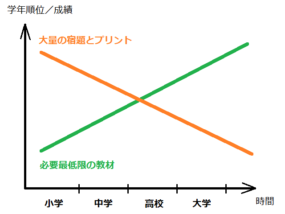
教材の優先順位を守る!
テストまであと3週間。人によっては2週間しかありません。
時間が限られています。
そこで、まず、何から取り組むべきか、優先順位を決めておきましょう。
ここで、
「学校のテストは学校の先生が作る」
という原理原則を忘れてはいけません。
ということは、学校から配られた順に取り組むのが基本です!!
つまり次の優先順位で取り組みましょう。
- 学校の教科書と授業ノート(授業プリント)
- 学校で配られたワークや問題集
- 学校で配られた追加プリント
- 塾のテキスト
- 塾で配られた追加プリント
なお、1~3は、学校の授業の進度に合わせて進めましょう。
3日以内に学校に追いつく!
例えば今日、学校の英語の授業で Unit0の Part1 を習ったとしましょう。
そしたら3日以内にジョイフルワークで Unit0のPart1 をやってください。
それが1周目です。
3日以上遅れたら、ちょっとヤバイかも。
日々の勉強をサボっている、ということになります。
テスト週間(部活休止期間)に入る前に、まずはそこまで追いついておきましょう。
サボった分は早いうちに巻き返しましょう。
学校の教材は2~3周やる!
上の基本ができていれば、テスト週間に入ったらすぐ2周目に取り組めます。
テスト週間になってから1周目に入るようでは、まさに周回遅れ。
その時点でかなり出遅れています。
ちなみに、最も無意味なのが1周しかやらないこと。
うろ覚えだから「やったつもり」「努力したつもり」になるだけで、まるで点数が取れません。
中学のテストは「正確に」「速く」記述できることが求められます。
ですからうろ覚えでは点数になりません。
それが小学校までとは違う所です。
「正確に」「速く」できるためには、同じものを2~3周くりかえして手の動きを速くしておくことです。
数の多いものこそ毎日コツコツやる!
英単語や漢字はもちろん、社会の用語や人物名、理科の用語や元素記号などなど、暗記の数が多いです。
こういう数の多い暗記モノは、「毎日コツコツ」が基本です。
テスト週間になってから、いきなり社会や理科の「漢字書き取り」を始める人がいます。
もちろん、かなり手遅れです。
そうなる前に、今からでも毎日コツコツ覚えていきましょう。
その日、学校の授業で出て来た新しい用語や単語について書き取りすれば、1日せいぜい10個くらいで済むでしょう。
「覚えたはずなのに、テストで言葉が思い出せなかった・・・」
こういう人は、漢字の書き取りだけでテスト本番を迎えてしまった人です。
肝心の「用語の意味」や「用語の使い方」まで、学習が進まなかったのでしょう。
テスト週間は、単語や用語を覚える期間ではありません。それでは遅いです。
テスト週間は、穴埋め問題や文章題を解く訓練期間です。
テスト週間に入る前に単語や用語を覚えていなければ、それができません。
教科書とノートをじっくり読む!
信じられないかもしれませんが、教科書を読まない生徒が意外と多いです。
例えば、小学生の頃に「音読カード」などを与えられ、宿題で教科書の音読をやらされたでしょう。
このように小学校の時代に「教科書をよく読む習慣」が身についたはずなのですが・・・
教科書を読まない生徒に話を聞くと、小学生の時代に音読の宿題が無かったと言います。
学校の先生から教科書の音読するような指示も受けたことが無かったと言います。
本当でしょうか?
そういう小学校を見たことが無いのですが・・・
まぁ、だいたい同じクラスだった別の子に聞くと、音読の課題があったと言うことが多いのですが。
もしそうだどすると「教科書を読まない子」=「学校の先生の話を聞かない子」なのかも?
何はともあれ、学校のテストでは教科書のどこから出題されても文句が言えません。
資料の写真やグラフはもちろん、脚注や章末ページまで、隅から隅まで要チェックですよ。
大人になれば、渡された資料にすべて目を通して次の会議までに覚える、なんて、毎日のようにありますよ。
【禁止事項】「0周目」の繰り返しに要注意
最後は「やってはいけない」ことです。
「YouTube見ながら」
「スマホの着信を気にしながら」
などなど・・・
気が散っている状態で取り組んだものは「0周」扱いです。
また、次のようなことも禁止です。
「教科書を見ながら回答欄を埋めた。」
「すぐに諦めて答えを写した。」
「自分で考えず、例題を見ながらパズル感覚で回答欄を埋めた。」
これらは「やっつけ作業」というものです。
いくら「やる気」があったとしても、こういうのは勉強とは言いません。
塾長はよく「やる気と勉強は関係ない!」と断言しておりますが、これが理由の1つです。
つまり、
- 注意散漫
- 穴埋め作業(やっつけ作業)
という状態はダメです。
ページが進んだとしても、勉強時間としては0時間です。
頭に入らないような取り組み方は「勉強」とは言いません。
そういう状態で進んだページは、どれもゼロカウント、つまり「0周目」です。
学校のテストで同じような問題をパッと出されても
「あれ、何かやったような気がするんだけどなぁ。」
という言い訳ばかりで、解くことはできません。
頭に入っていませんから。
「やってる」と言いながら、実際はにはずっと「0周目」を繰り返す。
そんな状態になっていませんか?
たとえば、中学生でスマホを持っているお子さんの、だいたい9割がこれ。
要するに、無意味なことをしない。ということ。
人間は自分の意思で覚えようとしたものしか頭に入りません。
勉強は自分の意思でしか行えません。
作業ではなく勉強をしましょう。
さて、ここまでが勉強の仕方の「基本」でした。
基本がしっかりしていなければ応用へ進むことができません。
できるだけ早めにマスターしましょう。
最後に付録として、テスト範囲の「予想」です。
1学期中間テストの範囲(めやす)
この時期のテスト範囲について、ヒーローズ植田一本松の近隣の中学校の傾向です。
なお、学校のテストは学校の先生が作りますから、学校の先生の話をよく聞きましょう。
成績どうこう言う前に、まず、人の話をしっかりと聞く、配られたプリントを確認する、が基本です。
それでは下の注意事項をよくお読みの上、ご参考までにお読みください。
免責と注意事項
- ヒーローズ植田一本松校の近隣の中学校を想定していますが、あくまでも塾長の個人的な予想です。なんら保証されるものではありません。
- 中学校とは何ら関係がありません。このブログの記事について中学校へ問い合わせてはいけません(中学校への迷惑行為となります)。
- 実際のテスト範囲は学校から配布される資料で確認してください(テスト前10日~1週間前に学校からテスト範囲表が配られることが多いです)。
上記に合意した方のみ、下をお読みくださいませ。
中学1年生 テスト範囲の目安
| \ | 教科書 | 単元 |
|---|---|---|
| 英語 | ~P17 | Unit0 ~ Unit1 アルファベット 放送問題 |
| 数学 | ~P55 | 第1章「正の数・負の数」すべて または「素因数分解」まで |
| 国語 | P14~24, 32~40, 27, 272 | 「ふしぎ」「桜蝶」 「自分の脳を知っていますか」 文法:「言葉の単位」 |
| 理科 | ~P40 | 「種子を作らない植物」まで |
| 地理 | P9~27 | 「世界の地域構成」 「日本の地域構成」 |
| 歴史 | – | なし ※ここ数年は地理から進める傾向 |
中学2年生 テスト範囲の目安
| \ | 教科書 | 単元 |
|---|---|---|
| 英語 | 中1:P112~ 遅:P108~ 中2:~P20 |
中1:Unit11~ 遅: Unit10~ 中2:~Unit1放送問題 |
| 数学 | 中1:なし 遅:P200~ 中2:~P33 |
中1:なし ※遅:「立体の体積と表面積」~ 中2:第1章すべて ※遅:「単項式の乗法・除法」まで |
| 国語 | P14-35, 40, 288-291 | 「虹の足」「タオル」 「間違えやすい漢字」 文法:「活用のない自立語」 |
| 理科 | 中1:P234~ 遅:P220~ 中2:~P37 |
中1:「地層」~ ※遅:「地震」~ 中2:第1章すべて (「酸化」の前まで) |
| 地理 | P120~146 遅:P106~146 |
「オセアニア」~第3編第1章まで (「地域調査の方法を学ぼう」まで) 遅:「南アメリカ」~ |
| 歴史 | P78~117 遅:P72~94 |
「倭寇」~「幕藩体制」 遅:「モンゴル帝国」~「室町文化」 |
中学3年生 テスト範囲の目安
| \ | 教科書 | 単元 |
|---|---|---|
| 英語 | 中2:P118~ 遅:P100~ 中3~P28 遅:~P17 |
中2:Let’s Read3 ~ 遅:Let’s Read2~ 中3:~Unit2 遅:~Unit1放送問題 |
| 数学 | 中2:P172~ 遅:P168~ 中3:~P37 |
中2:「箱ひげ図」~ 遅:「確率の利用」~ 中3:第1章「式の展開と因数分解」すべて |
| 国語 | P4~28, 134~139 | 「春に」「なぜ物語が必要か」 「風景と心情」(漢詩) 文法:「助詞」「助動詞」 |
| 理科 | 中2:P256~ 中3:~P49 |
中2:第3章「天気の変化」~ 中3:~第3章「物体の運動」まで (「作用と反作用」まで) |
| 地理 | P244~273 | 「東北地方」 「北海道地方」 |
| 歴史 | P186~217 遅:P178~206 |
「明治維新」~「第一次世界大戦」 遅:「自由民権運動」~「明治時代の教育と文化」 |
進級して最初のテスト。
頑張っていきましょう!
進学実績
卒塾生(進路が確定するまで在籍していた生徒)が入学した学校の一覧です。
ちなみに合格実績だけであれば更に多岐・多数にわたります。生徒が入学しなかった学校名は公開しておりません。
国公立大学
名古屋大学、千葉大学、滋賀大学、愛知県立大学、鹿児島大学
私立大学
中央大学、南山大学、名城大学、中京大学、中部大学、愛知淑徳大学、椙山女学園大学、愛知大学、愛知学院大学、愛知東邦大学、愛知工業大学、同朋大学、帝京大学、藤田保健衛生大学、日本福祉大学
公立高校
菊里高校、名東高校、昭和高校、松陰高校、天白高校、愛知教育大学附属高校、名古屋西高校、熱田高校、緑高校、日進西高校、豊明高校、東郷高校、山田高校、鳴海高校、三好高校、惟信高校、日進高校、守山高校、愛知総合工科高校、愛知商業高校、名古屋商業高校、若宮商業高校、名古屋市工芸高校、桜台高校、名南工業高校、菰野高校(三重)
私立高校
愛知高校、中京大中京高校、愛工大名電高校、星城高校、東邦高校、桜花学園高校、東海学園高校、名経高蔵高校、栄徳高校、名古屋女子高校、中部第一高校、名古屋大谷高校、至学館高校、聖カピタニオ高校、享栄高校、菊華高校、黎明高校、愛知みずほ高校、豊田大谷高校、杜若高校、大同高校、愛産大工業高校、愛知工業高校、名古屋工業高校、黎明高校、岡崎城西高校、大垣日大高校
(番外編)学年1位または成績優秀者を輩出した高校
天白高校、日進西高校、愛工大名電高校、名古屋大谷高校
※ 成績優秀者・・・成績が学年トップクラスで、なおかつ卒業生代表などに選ばれた生徒
名古屋市天白区の植田で塾を探すなら個別指導のヒーローズ!!
★ 直接のお問い合わせ ★
――――――――――――――――――――――
個別指導ヒーローズ 植田一本松校
〒468-0009
名古屋市天白区元植田1-202 金光ビル2F
TEL:052-893-9759
教室の様子(360度カメラ) http://urx.blue/HCgL