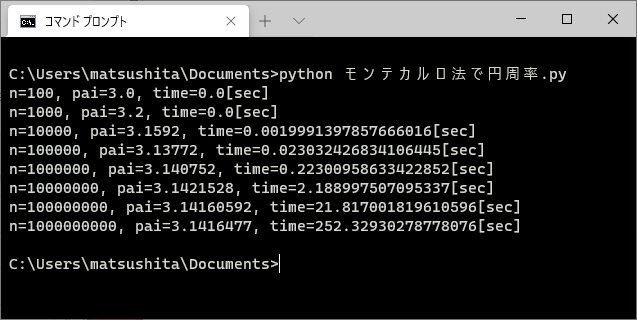
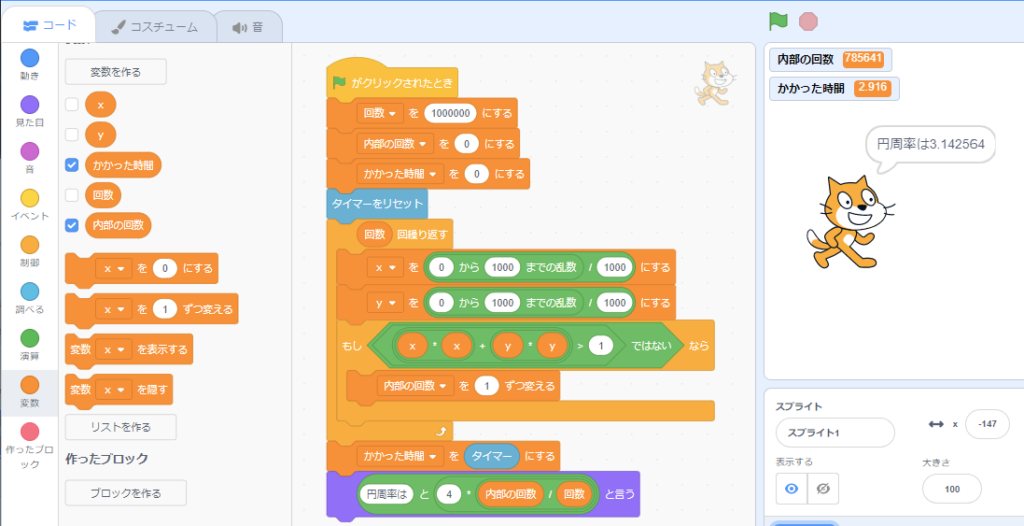
塾長です。
今日のお話は9割実話です。学校名や人名は仮称に置き換えてあります。
第1話 (入部までの回想)
心臓破りの坂道
今日から一応、高校生だ。
目の前には、長く曲がりくねった急な坂道が、ひたすら続いている。
これを登りきれば、東京科学大学第二高校の門にたどり着ける―――はずである。
自転車のギアを1段、また1段と軽くしていく。
それなのに足がどんどん重くなる。
登れば上るほど勾配がきつくなる。
いっこうに学校にたどり着ける気がしない。
「何なんだ、この坂道は。」
歯を食いしばり、ハンドルを力いっぱい握り、これでもか、というくらい足に力を込める。
まだ4月なのに、額から汗が垂れてくる。
そもそも、この高校には来る予定ではなかった ―――。
公立高校が第一志望だったのに、合格できなかった。
そしで滑り止めとして受験したこの高校に来る羽目になったのだ。
「ああ、なんで通学からして、こんなに辛いんだよ。
これはきっと、受験に失敗した僕への罰なんだ。」
そんなふうに卑屈に考え始めた。
そして、この高校を受験した日のことを思い出した。
あの日は雪で、とても寒かった。
しかし気持ちは落ち着いていて、程よい緊張感で、むしろ心地よかった。
根拠のない自信に満ちていた。
雪のせいで足元が少し滑ったが、そんなジンクスなど全く気にしなかった。
「うちと公立高校の両方に合格したら、どちらに進学しますか?」
そんな面接官からの質問にさえ、
「もちろん、公立高校の方が第一志望なので、そちらに進学します!」
などとキッパリ、正直に回答したっけ ―――。
でも、こんな坂があるなんて、記憶になかったぞ。
ああ、そうか。
あの時は雪だったから、池谷くんのお母さんが一緒に車で送ってくれたんだった。
車内で色々と話をしている内に門の前に到着してしまったから、この坂のことを記憶していなかったのだ。
何はともあれ、きつい坂だ。
僕はもともと体力がない方だ。
中学のマラソン大会は、いつも最後尾のグループだった。
本当にこれから毎日、通学できるのだろうか。
第一、この坂にたどり着いた時点で、既に10Kmも自転車で走ってきているのだ。
完全にくたくただ。
こんな状態の僕なんかが、これから毎日、本当に通学できるのだろうか。
この高校のこと、ほとんど何も知らないまま入学することになってしまったんだな。
なんだか不安ばかり増大して来た。
ここを一緒に受験した池谷くんは、めでたく第一志望に合格した。
池谷くんとは合格発表を一緒に見に行ったっけ。
帰りも一緒だったはずだが、どうやって帰ってきたのか、ほとんど覚えていない。
きっと帰り道はずっと僕に気を遣ってくれていたのだろう。
池谷くんは頭が良いし、いいヤツだし、合格して当然だ。
今頃、あっちはあっちの学校で入学式だろう。
ここ最近、僕の唯一の楽しみといえば、進学祝いに買ってもらった、この自転車だ。
第一志望には合格できなかったけど、それでも買ってもらえた。
受験の失敗に両親が同情したのだろう。それでも嬉しかった。
24段ギアのフル装備。
どんな道もスイスイ走れるマシンだ。
体力は無いが、サイクリングは唯一好きなスポーツだ。
これで通学するなら毎日が楽しいだろうと思っていたのに・・・。
「本当に、何、なんだ、この、坂は。
登校、する、だけで、こんな、に、大変だ、とは、聞いて、ない、ぞ。」
手が痛くなるほど、ドロップハンドルをずっと握りしめている。
ものすごく低い姿勢で、全身の力を足へ伝える。
路面が目の前に迫ってくるようだ。
何とも言えない圧迫感を感じてしょうがない。
「あー、もうっ。」
と、ため息と苛立ちを混ぜたような声を出してしまった。
そして、とうとう自転車から降りてしまった。
これより軽いギアは、もう無いのだ。
もう限界だ、ペダルをこぐ力が出てこない。
そもそも、ここに来るまでに、結構な距離を走ってきたんだ。
ブレーキをぎゅうっと握ったまま、かろうじて自転車を支えて立ち尽くすと、そのままうなだれた。
「ふぅー。」
下を向いたまま深く呼吸をした。
その姿勢のまま、横目でちらっと周りを見てみると、けっこう、みんな自転車から降りている。
あれ。
なぁんだ。
先輩たちにとっても辛い坂らしい。
ならば、このまま自転車を手で押して行っても別におかしくはないか。
冷静に考えてみれば、そりゃそうだな。
少し気が楽になって、顔を上げた。
すると、ちょうど視線の先に、丘の中腹で白く映える校舎が見えた。
あそこがゴールか。
この勾配が、まだまだ100mくらい続くのか。
歩くことにして正解だ。
そう思った矢先、
「あっ。」
思わず声が出た。
景色の中の、ある一点だ。
白い校舎の屋上だ。
直ぐに分かった。
青い空をバックに、眩しく、銀色に輝くドーム。
「まさか、あれは・・・天文台じゃないか!」
そのまま視線が釘付けになった。
坂を歩く生徒たちが次々に横を通り過ぎていく。
そうか、そうか。
なぁんだ、良いこともあるじゃないか。
胸がかーっと熱くなった。
もうゴールしてしまったかのような、清々しい気持ちになってきた。
受験がどうのこうのという記憶が、その瞬間から過去になってしまった。
すっかりどうでも良くなっていた。
あれを使えるんだ!
一生懸命勉強して天文学者になるのが夢だ。
天文学者になって、天文台で毎日観測するんだ。
そのために受験が終わるまで天体観測を我慢して、勉強してきた。
本当に我慢して勉強したんだ。
でも受験は失敗した。
それで夢が遠のいたと思っていた。
そうじゃなかったんだ。
もう、いきなり使えるのだ。
まだ少し息が荒い。
それでも肩を上下させながら、自然と足が動き出した。
もしかしたら、最初から僕はこの高校へ来た方がよかったのかもしれない。
いや、そうなるべくして、僕はこの高校へ来る運命だったのだ。
あの校舎を目指すのだ。
私立高校だから、きっと設備が贅沢なんだろう。
あぁ~、早く中に入ってみたいなぁ。
屈折望遠鏡かな、反射望遠鏡かな。
新しい友達や担任の先生がどんなだろうという想像をすっ飛ばして、今や放課後のことしか考えていない。
あの天文台を使っている部活とか、あるのかな。
レクリエーションの時、さっそく部活のパンフレットをもらいに行こう。
天文部だろうか。
でも、高校では、それ系の部活は「地学部」が多いと聞いたことがある。
天体観測よりも気象や岩石の観察がメインだったらどうしよう。
いや、あんな立派な天文台があるくらいだから、天体観測をやらないわけないでしょっ。
ニヤニヤしながら自転車を押し続けた。
しばらくして、グランドが見え出した。
野球部やラグビー部が朝練をしている。
そういえば、運動部が強くて有名だ。
野球は甲子園、ラグビーは花園に行くくらいの名門校だ。
僕でも、そのくらいは知っているぞ。
「よし!」
と、再び自転車にまたがった。
はやる気持ちから、思いっきりペダルを勢いよく漕ぎ出した。
しかし、やっぱり坂はきつかった。
「だめだ、こりゃ。」
と小声で言うと、10メートルもしないうちに、また自転車から降りてしまった。
「ま、いっか。」
ちょっと恥ずかしいと思ったが、それも一瞬で、周りの生徒と同じように、また歩きだした。
ホームルーム
入学式、新入生歓迎会、そしてクラスで最初のホームルーム。
高校生活で初めてのイベントが目白押しだったが、それらは瞬く間に終わった。
どの生徒たちも、なんとなく教室で、だらだらと歓談していた。
初日からさっさと帰宅してしまうのが物足りないのだろう。
僕も何となく教室に残っていた。
新入生歓迎会で配られた資料を読んでいた。
廊下や中庭から帰宅する生徒たちの話し声が聞こえてきた。
入学式の後の歓迎会、本当に楽しかったなぁ。
応援団の演舞は、ものすごく迫力があった。
運動部が全国レベルだと、応援団も凄いものになるってことなのかな。
あんなの初めて見た。
でも、文化部の紹介はほどんどなかった・・・
やっぱり部室へ直接見に行くしかないかぁ。
余韻に浸りながらパンフレットの部活紹介をパラパラめくっていた。
「あっ」
地学部の紹介ページに目が留まった。
そうか、あの天文台はきっと地学部が使っているんだな。
天文部は無かったし、写真部は写真だけだろうし。
すると突然、後ろの席の須藤が話しかけてきた。
「なぁ、部活どこに入るか決めた?」
須藤はとても気さくで、今朝も向こうから話しかけてきた。
「あー、うん。
地学部にしようかと思ってる。
星を見たりするのが好きだから。」
「へー、そうなんだ。
俺も星を見るの好きだぜ。
俺の家はけっこう山の方だから、星がきれいに見えるんだ。
スバルとかオリオン座とか。今は北斗七星が見やすいな。
けっこう知ってるだろ、俺。」
「あー、いいなぁ。
でも、山の方って、どこから来てるの?」
「倉渕村。知ってる?
まぁ、榛名山に行く途中くらい。
自転車と電車で1時間以上。
2年になったらバイク通学しようかなって思ってる。
この学校、バイク通学ができる数少ない高校だから。」
「へぇ、バイクOKなんだ。初めて知った。
僕の家でも、小さい頃はよく星が見えたんだ。
周りが田んぼだらけだったからね。
でも最近はコンビニとか建物が増えて、だいぶ見えなくなってきたよ。」
「ふーん、都会はいいねぇ。
コンビニなんて、うちの近くには無いよ。
で、どこから通ってるん?」
「僕は前橋から。
ここまで12Km、自転車で1時間くらい。
道がまだよくわからなくて、慣れたらもう少し速く来れると思うんだけど。」
「12Kmなんて、近い方だよ。
俺なんか駅から家まで、帰りはずっと上り坂だぜ。
ま、足が鍛えられていいけどね。
俺はサッカー部に入るからさ、もっと強くならないと。
小学生のころからサッカーやってきて、中学では選抜チームに入ってたんだぜ。
それでサッカーをやりたくて、この高校を単願で受けたんだ、俺。」
「サッカーできるなんて、すごいね。
僕は正直言うと、運動は、あまり得意じゃないんだ。」
「お前、なんか見るからに頭よさそう、勉強してそうだもんな。
もしかして併願か?」
「あぁ・・・まぁ。
実は公立高校を落ちちゃってね・・・
まぁ、ここには天文台があるって知って、今はそれが楽しみだよ。」
「本当に星が好きなんだな。」
あの坂道の途中で、天文台に気が付いてよかった。
もしも気が付かなかったら、きっと、後ろ向きの気持ちのまま教室に来ていただろう。
そしたら、須藤との会話も、こんなに続かなかったかもしれない。
僕は自分から他人に話しかけていけるような人間じゃない。
どちらかというと聞き役だ。
初対面の人とは何を話したらよいかよく分からなくて、いつも新学期は少し緊張する。
でも、須藤とは気軽に話ができた。
須藤は本当に良い奴だ。
なんか、この高校のことが好きになれる気がする。
よし、僕も須藤を見習って、他の奴にも話しかけてみるか。
前の席のやつが窓の外を見ている。
「やあ、確か君は佐橋くんだったかな。
僕は重松、よろしく。」
「よろしく。」
あれ。
あまりこっちを見てくれない。
きっと僕と同じで緊張しているのかな。
「えっと、どこの中学から来たの?」
すると僕の方を一瞬ちらと見て
「北中。」
と答えた。
え。
何で目を逸らすんだろう。
なんか嫌われたのかな。
「レクリエーションは楽しかったね。」
「そうですね。」
「どこか部活に入るのかい?」
「どこにも。」
「あ、じゃあ何か趣味で忙しいとか。」
「・・・別に。」
自分の会話力のなさに焦りつつ、もうそろそろ引き際とも思ってきた。
須藤を見習うどころか、気分が嫌になっていた。
何こいつ!
大人しそうに見えるが、なんか態度がむかつく。
とにかく、これ以上は話しかけない方が良さそうだ。
でも、自分から話しかけた手前、何とも困った。
「おう重松、じゃ、俺はサッカー部見てくるわ。また明日な。」
「あ、うん、また明日。」
須藤のあいさつで救われた。
僕もその勢いに乗じて教室を出た。
「じゃあ、僕もそろそろ行こうかな。」
もちろん地学部へ向かった。
理科室の奥の部屋
あ、ここかな。
”理科実験室が地学部の部室です”
ってパンフレットにあるから、多分ここだよね。
教室と同じ棟で、けっこう近いな。
さっそく実験室の戸に手をかけた ―――
ガラガラ・・・
思ったよりも大きな音がしてしまった。
「す、すみません。地学部の見学に来ました。」
慌てて挨拶をした・・・
しかし返事がない。
そのまま1歩踏み込んで実験室の中を見回したが、誰もいないようだ。
とりあえず、さらに2、3歩ほど中に進んだ。
ひんやりした空気が漂っていた。
あぁ、この冷たい感じ、理科実験室らしい。
理科実験室は、やっぱりいいなぁ。
部屋の隅が少し埃っぽくて、いくつの机や椅子が部屋の隅にまとめられている。
授業ではあまり使ってないのかな。
実験机の並ぶ向こうに、無駄なほど大きな黒板が見える。
少なくとも毎日使っている感じではなさそうだ。
少しすると、奥の方から人の話し声が聞こえてきた。
声の方向を見ると「理科準備室」と書かれたドアがあったので、そのままドアの方へ向かった。
何やら中でワイワイガヤガヤ、楽しそうに話している。
ここが本当の部室なのか。
よし、今度はちゃんと挨拶をして入ろう。
コンコン
「すみません、地学部の見学に来ました。」
そのとたん、部屋の中が静まり返った。
シーンとして、それっきりだ。
意外な反応に、時間の流れだけが存在感を増す。
本当は5秒くらいの間だったのだろうか・・・
ガチャリ
ドアが開くと、その向こうにカマを持った男が立っていた。
え、カマ!?
まったく想定外の景色に、固まるしかなかった。
目と目が合っちゃったけど、どうしよう・・・。
この人、先輩? ・・・だよね。
僕は何をされるんだろう。
しかし数秒もしないうちに、ドアをバタンと閉められてしまった。
何が何だか分からず、立ち尽くすしかなかった。
地学部にカマ?
何で?
部屋の中で何してたんだろう。
やばい、来る部屋を間違えたかもしれない。
「おい、どうするどうする、見学だってよ。」
「え、まじで、もう来たの!?」
「え、新入生?すごいじゃん。」
「男、女?」
「男だったよ。」
「お前、部長だろ、部長が行けよ。」
中から、何やら騒がしい声が聞こえだした。
どうやら、場所は間違っていなかったようだ。
そして再び静かになったと思うと、またドアが開いた。
ガチャリ
「こんにちは。よく来たね。
僕は部長の水前です。」
今度はさっきより少し背の高い先輩だ。
ちらりと振り返って、部屋の中を隠すように続けた。
「あぁ、まぁ、奥は狭くてごちゃごちゃしてるから、実験室で話をしよう。
ちょっと、そこで座って待っててね。」
と言って、再びドアの向こうに行ってしまった。
「あ、はい。よろしくお願いし・・・」
言われた通り待つことにして座っていると
ガラガラガラ・・・
背後から窓の開く音がした。
今度は何!?
振り返ると、リュックを背負った男が、窓から実験室に侵入して来ているではないか!
え、ここは2階のはずなんだけど・・・。
びっくりして、そのまま静観していた。
この人も、先輩?だよね。
窓から部屋に降り立つと同時に、そのリュックの男が話しかけてきた。
「あ、もしかして新入生?
もう見学に来てくれたんだ。
うれしいな。」
「あ、はい・・・。」
唖然としていると
「あ、これ?
これは秘密のショートカット。
この窓から来ると、隣のキャンパスから最短で来れるんだよ。
だから、この窓のカギは絶対に閉めちゃダメだよ。
あと、先生にも内緒ね。
見つかると怒られるから。」
「あ、はい・・・。」
よく見ると爽やかそうな先輩だ。
それはそうと、いったい、ここは2階なのに、どういうワケだろう。
窓の外を少しのぞいてみた。
なるほど、隣の大学の非常階段の手すりに立てば、この窓に足が届くという感じ。
こちらの校舎も壁沿いに配管があって、いざという時には、そこも足場になるようだ。
でも高いところが苦手な人は、ダメだろうな。
「俺は地学部の村山、よろしく。
君は?」
「新入生の重松です。
よろしくお願いします。」
「うん、重松君ね。
で、まだ誰もいなかった?」
「あ、いえ、部長の水前さんから、ここで待つように言われました。」
「あ、そう。
何やってるんだろ。
ちょっと見てくるね。」
そう言って、この人もまた、奥の部屋に消えていってしまった。
「おい、新入生が待ってるぞ。何やってるの?」
「いや、散らかってて片付けようと。」
「でも実験室で待ってるぞ。」
「いいよ、とりあえず、呼んじゃえ。」
「いや、いきなりここは見せられないだろ。」
ガチャリ
ドアがまた開いて人が出てきた。
「やぁ、待たせたね。」
水前さん、村山さん、さっきのカマの先輩と、続いて女の先輩も出てきた。
「やー新人くん、よく来たね~。
ごゆっくり~。
あたしは用事があるから、先に帰るね~。」
最後の女の先輩は、そのまま実験室を出て行ってしまった。
「やあ、さっきは変なところを見せてしまったね。
びっくりした?
僕は永田っていうんだ、よろしく。」
カマの先輩、しゃべれるんだ。
「あ、はい、よろしくお願いします。」
それにしても、この段取りの悪さというか、適当さというか、ダレた感じは何だろう。
歓迎されているのか、いないのか、なんだか微妙な空気だ。
部長の水前さんが話を始めた。
「えー、それで。
僕ら地学部は、地質班、気象班、天文班、それと情報処理班の4つの分野で活動しているよ。
さっき帰っていった野口は情報処理班かな。
あ、彼女だけは高等部3年ね。
うちの大学にそのまま進学するから、まだ余裕があるはずなんだけど、なんかいつも忙しそうで、僕らの間でも謎ですな。
それはさておき、君はどうして地学部に来たんだい?」
「はい、僕は天体観測がしたくて。
中学の時も友達と観測会をやっていました。」
「そうか、すると天文班ってことになるかな。
じゃ、僕と同じだね。」
水前さんからそうに言われて嬉しくなった。
急に期待が膨らんできて、思わず質問してしまった。
「やっぱり天体写真とか撮るんですか?
天文台の望遠鏡を使ったりとか?」
「うん、僕自身も望遠鏡やカメラを持っているからね。
最近はほとんど時間がなくて、やってないけど。
あと、他の班が手薄になってるときは手伝うから、気象にも詳しいよ。」
すると村山さんが話を始めた。
「ねぇ、山とか興味ある?
山は良いよ~。」
「あ、こいつは地質班ってことになってるけど、実際には山岳部がないから地学部に来たっていう感じかな。
山登りのついでに化石を掘りに行く感じだよ。」
すかさず水前さんが説明してくれたので、話がつながった。
「いやいや、ちゃんと化石もやってるって。
この近くは昔の炭坑跡があってね、裏山からは葉っぱの化石も見つかるんだよ。」
「へぇ、そうなんですか。こんな身近なところで化石が採れるんですね。」
村山さんも地学部らしい人で安心した。
少し場に馴染んできた気がする。
そこで、さっきから無性に気になっていることを聞いてみることにした。
「あの、永田先輩は、さっきは何でカマを持ってたんですか?」
「あ、いや、普段は部外者なんて来ないから、怪しい人だったら撃退してやろうと思ってね。
ふふふ・・・」
ケガがなくて良かったぁ・・・ちょっと凍り付いた。
「いやいや、冗談、冗談。
カマは僕の相棒だからさ、何となく持ってただけ。
別に深い意味はないよ。
化石を掘るときにカマは大切なのさ。
これからの季節、山を歩くにも化石を掘るにも草が邪魔だからね。」
永田先輩はどうやら地質班のようだ。
「気象班はいないんですか?」
「あー、えーと、今の部員の中で気象班はいないかな。
ただ、顧問の教授が気象班出身のOBで、何らかの活動は必ずやらされるんだよ。
だから何班でも必ず気象班には駆り出されます。
あ、でも、普段は自分たちの好きな活動をちゃんとやらせてくれるから、安心してね。」
けっこうリーダーシップのある顧問がついているんだな。
色々と積極的に活動してそうだ。
きっと凄いんだろうな。
ということは・・・
「あの、できれば、天文台を見せて欲しいのですが。」
急なお願いとは思った。
でも、やっぱり見たいものは見たい。
すると水前さんは、村山さんや永田さんと目で会話するように視線を移した。
そして僕の顔をうかがいながら口を開いた。
「えーと、天文台の見学ね。
そうだよねぇ、見たいよね。
でも、えーと、僕らは大学2年で、研究室のプレセミナーが始まるから、もうすぐ地学部を引退するんだよ。
だから次期部長と副部長はもう決まっている。
もう少ししたら来るから、ちゃんと紹介するよ。
きっと彼らが親切に対応してくれるだろうから、お楽しみにね。」
さっきの間は何だろうと思ったけど、きっと、もったいぶっているんだろうな。
「はい、楽しみです。」
「あ、だからといって、別に僕らは遊んでるわけじゃないよ。
研究室に行く前に、なんとなく皆で集まることが多くてね。」
なるほど。
要するに、ご隠居さんたちが部室をたまり場にしてるってことか。
和気あいあいとした感じで、楽しそう?
って思えばいいのかな。
しばらくすると、理科実験室に、2人の先輩たちが入ってきた。
ガラガラガラ・・・
「あ、こんちわっす。
今日は奥じゃなくて、ここに集まってるんですね。
おや、もしかして、もう新入生ですか!?」
水前さんが答えた。
「おー安住、待ってたよ。
ちょうどお前らのことを話していたところだ。」
「こんちわっす。
新入生って、今年は早いですね。」
「えーと、こちらが見学に来てくれた新入生の重松くん。
重松くん、こっちが安住くん、次期部長で、こっちが石原くん、次期会計だよ。」
「はい、よろしくお願いします。
パンフレットの部活紹介を見て、見学に来ました。」
すかさず挨拶をすると、石原さんが答えた。
「おー期待の星じゃん!
重松くんね、よろしく。
僕は大学部の1年で、僕らの学年は俺ら2名しかいないんだ。
だから、もう部員が増えると思うと、うれしいね。」
「石原くん、石原くん、まだ見学だよ。
重松くん、まぁ軽い気持ちで見学していってよ。
仮入部期間は色々と他も見てきた方が良いしね。」
安住さんは冷静な人みたいだ。
「安住くん、重松くんが天文台を見学したいそうだよ。」
水前さんが話を進めてくれた。
「あー、天文台ね。
天文台かぁ・・・ってことは、天文班希望なのかな。
さっきは軽い気持ちで、なんて言っちゃったけど、けっこう本命で来てくれたんだね。
うれしいなぁ・・・。
なら天文台を見たい・・・って話になるよね・・・なるほど・・・。」
すると横から石原さんが割って入った。
「うん、天文台はね、仮入部期間が終わって、正式に入部した人だけに見せたいんだよ。
観測機器だからさ、一般公開を気軽に、みたいには行かないからさ。
それまで楽しみにしていてくれ。」
「あ、はい・・・わかりました。」
あからさまに残念な表情が顔に出てしまった。
やっぱり、それが伝わってしまったようだ。
「ま、まぁ、今はカギを持ってないから、どちらにしろ入れないから。
また後日、ちゃんと見学会をするってことで。」
安住さんがフォローするように言ってくれた。
「屋上だけでよければ、明日にでも見学できるよ。
外観だけで良ければ、明日また見に来るかい?
屋上に行けば近くで見られるよ。」
「あ、はい、お願いします。」
「地学部だけなんだ、屋上が使えるのは。
地学部の特権みたいなもんかな。
それって、ちょっとすごいと思わない?」
「あ、そうですよね。
小学校や中学校では、基本的に生徒は屋上に入れませんでした。
言われてみれば、一度も行ったことないです。」
「な、そうだろ。
しかも、天文台の下が準備室になっていて、そこも使えるんだよ。
理科実験室、理科準備室、屋上に天文台。
地学部の使える設備って、けっこう贅沢なんだよ。
ま、そういうワケだから、明日また来て欲しいな。」
「ありがとうございます。それはぜひ、お願いします。」
ちょっとワクワクしてきた。
天文台の中に入れないのは残念だけど、それは後のお楽しみ、ってことで良いかな。
その後、僕は先輩たちの歓談の中心に引っ張り出され、色々と質問攻めになった。
「重松くんはどこから来てるの?」
「いつから星を見てるの?」
通学のこと、受験のこと、星のこと。
色々な話しができた。
そして、あっという間に夕方になってしまった。
「さて、そろそろ解散にしよう。」
とても気さくな先輩たちで楽しかった。
下校時刻になった。
帰りは下り坂。
自転車が自動的に走ってくれる。
とても楽ちんで気分爽快。
明日も楽しみだ。
あとがき
行ってみたら、やってみたら、意外にも最高だった。
そういう人生の方が多いのかもしれません。
どこに行ったかではなく、何をしたか。
目の前に見える景色、あなたの目の前にいる人たち・・・そして今というこの時間。
それらを大切にしてください。
後で、それらがとても大切だったと気が付くでしょう。
進学実績
卒塾生(進路が確定するまで在籍していた生徒)が入学した学校の一覧です。
ちなみに合格実績だけであれば更に多岐・多数にわたります。生徒が入学しなかった学校名は公開しておりません。
国公立大学
名古屋大学、千葉大学、滋賀大学、愛知県立大学、鹿児島大学
私立大学
中央大学、南山大学、名城大学、中京大学、中部大学、愛知淑徳大学、椙山女学園大学、愛知大学、愛知学院大学、愛知東邦大学、同朋大学、帝京大学、藤田保健衛生大学、日本福祉大学
公立高校
菊里高校、名東高校、昭和高校、松陰高校、天白高校、名古屋西高校、熱田高校、緑高校、日進西高校、豊明高校、東郷高校、山田高校、鳴海高校、三好高校、惟信高校、日進高校、守山高校、愛知総合工科高校、愛知商業高校、名古屋商業高校、若宮商業高校、名古屋市工芸高校、桜台高校、名南工業高校
私立高校
中京大中京高校、愛工大名電高校、星城高校、東邦高校、桜花学園高校、東海学園高校、名経高蔵高校、栄徳高校、名古屋女子高校、中部第一高校、名古屋大谷高校、至学館高校、聖カピタニオ高校、享栄高校、菊華高校、黎明高校、愛知みずほ高校、豊田大谷高校、杜若高校、大同高校、愛産大工業高校、愛知工業高校、名古屋工業高校、黎明高校、岡崎城西高校、大垣日大高校
(番外編)学年1位または成績優秀者を輩出した高校
天白高校、日進西高校、愛工大名電高校、名古屋大谷高校
※ 成績優秀者・・・成績が学年トップクラスで、なおかつ卒業生代表などに選ばれた生徒
生徒・保護者様のお友達登録はこちら
LINE登録するとプレゼントがもらえます!
【会員限定】お子様の成績と可能性を伸ばす18個のノウハウ

塾関係者様のお友達登録はこちら
LINE登録するとプレゼントがもらえます!
「zoomで簡単。オンライン授業移行の教科書」
または個別対談も可

名古屋市天白区の植田で塾を探すなら個別指導のヒーローズ!!
★ 直接のお問い合わせ ★
――――――――――――――――――――――
個別指導ヒーローズ 植田一本松校
〒468-0009
名古屋市天白区元植田1-202 金光ビル2F
TEL:052-893-9759
教室の様子(360度カメラ) http://urx.blue/HCgL