塾長です。
いよいよ夏休みも後半です。
学生のキミたち、そろそろ読書感想文や自由研究に着手しましょう。
ということで、自由研究ネタを1つご提供します。
算数の研究です。
しかし、内容が深くてプログラミングもありますから、きっと中学生でも使えるでしょう。
算数や数学で「文章問題が苦手」という人には、特にチャレンジして欲しいです。
そもそも「かけ算」や「わり算」の意味とは?
もしも小学1年生や2年生から、次のように質問されたら、どのように答えますか?
- 「かけ算」とは何ですか?
- 「わり算」とは何ですか?
塾長は、次のように答えます。
- 「かけ算」とは「たし算の繰り返し」です
- 「わり算」とは「ひき算の繰り返し」です
なぜなら、
人類で初めて「かけ算」や「わり算」を発明した人は、きっと上のように考えたに違いない!
塾長は、そうに思うからです。
これをプログラミングで確かめていきたいと思います。
「たし算」で「かけ算」をプログラミングする
もしも「かけ算」が「たし算の繰り返し」なら、その通りに計算ができるはずです。
やってみましょう。
具体的な例から「かけ算」のパターンを考える
5×3の場合
例えば、5×3の計算を考えましょう。
5×3=5+5+5=「5を3個たす」=15(積)
ここで「たし算」の「+」記号は2個です。
つまり、
5を「3個」たすときは、たし算を「2回」使います。
たし算の回数は3-1=2回です。
7×6の場合
もう1つの例、7×6の計算ではどうでしょう。
7×6=7+7+7+7+7+7=「7を6個たす」=42(積)
ここで「たし算」の「+」記号は5個です。
つまり、
7を「6個」たすときは、たし算を「5回」使います。
たし算の回数は6-1=5回です。
「かける数」は「たした個数」
まとめます。
m×nの場合
一般化して、m×nの積を計算する方法を考えます。
上の2つの例から、これは「mをn個たす」です。
そして、たし算を使う回数は(n-1)回です。
つまり、
m×nとは、mに(nー1)回だけmをたし算すること
まとまりました。
スクラッチでプログラミング
それでは上のm×nの手順をプログラムにしてみましょう。
mにmをnー1回たす
これをプログラミングしたのが次です。
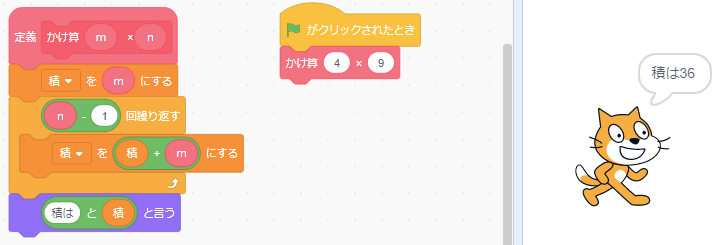
- 「積」という変数を用意して、それにmを代入
- 「積にmをたす」という処理を(nー1)回くりかえす
- 「積」を表示
試しに、4×9でプログラムを実行しました。結果は36で正しいです。
つまり「たし算」を繰り返せば、確かに「かけ算」を計算できることが分かりました。
そしてこのプログラムは、どんな自然数どうしのかけ算でも計算できます。
プログラムのカイゼン
ところで、このプログラムは1つ分かりにくい所があります。
「×n」なのに、繰り返す回数が「n-1回」です。
「かける数」と「回数」が1つズレています。
これを同じにできれば、もっとプログラムが分かり易くなります。
そこで、こう考えたらどうでしょうか。
変更前: 最初に「積」という変数を用意して、それにmを代入します。
変更後: 最初に「積」という変数を用意して、それに0を代入します。
こうすれば、繰り返し回数もnになります。
つまりプログラムがこうなります。
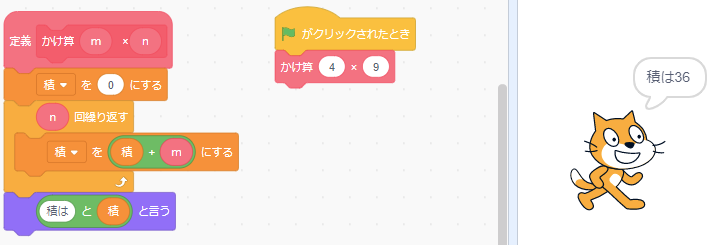
プログラムがシンプルで見やすくなりました。
「かける数」は「0にたした回数」だった!?
プログラムを見やすくするために、上のように改善しました。
逆に、このプログラムが行っている処理を式で表すと、どうなるでしょうか。
例えば、7×6の場合に戻れば、こうなります。
変更前: 7×6= 7+7+7+7+7+7+7
変更後: 7×6=0+7+7+7+7+7+7+7
単に「かける数」と「たす回数」が同じになるように工夫しただけですが、実は、こうした方が数学的にも良いことが分かっています。
それは「かける数」を3、2、1、0と小さくしていけば分かります。
変更前の考え方では、
7×3=「7に7を2回たす」
7×2=「7に7を1回たす」
7×1=「7に7を0回たす」
7×0=「7に7を?回たす」
となってしまい、7×0を考えることができません。
一方、変更後の考え方ならば、
7×3=「0に7を3回たす」
7×2=「0に7を2回たす」
7×1=「0に7を1回たす」
7×0=「0に7を0回たす」
となりますから、ちゃんと7×0=0も計算できます。
ちなみに0という数も人類が「発明」した数なのだそうです。
「ひき算」で「わり算」をプログラミングする
たし算と同じように、わり算についても考えてみましょう。
もしも「わり算」が「ひき算の繰り返し」なら、その通りに計算ができるはずです。
やってみましょう。
具体的な例から計算のパターンを考える
9÷3の場合
例えば、9÷3の計算を考えましょう。
9÷3=「9の中に3がいくつあるか?」=「9-3-3-3=0だから9から3を3回ひけた」=3(商)
ここで「ひき算」の「-」記号は3個です。
つまり、
9から3を「3回」ひき算できたから、商は3です。
12÷5の場合
もう1つの例、12÷5の計算ではどうでしょう。
14÷5=「14の中に5はいくつ?」=14-5-5=2だから2回ひけて4あまった」=2(商)あまり4
ここで「ひき算」の「-」記号は2個です。
まだ4余っていますが、3回目の引き算まではできません。
つまり、
14から5を「2回」ひき算できて4余るから、商は2、あまりは4です。
「商」とは「引くことができた回数」
まとめます。
m÷nの場合
一般化して、m÷nの商とあまりを計算する方法を考えます。
上の2つの例から、商は「mからnを引ける回数」です。
しかし、ひき算できる回数は、計算してみなければ分かりません。
1回引いてみて、まだ引けそうならもう1回引いてみて・・・という計算を繰り返します。
m-n=〇 もしも 〇>n ならば もう1回引ける・・・
という判断を繰り返してい良く計算です。
ですから、
わり算で商と余りを求めるとは、
m-n-n・・・-n=△ かつ 0≦△<n
k回引けたので商がk、余りが△
という処理をすること
まとまりました。
スクラッチでプログラミング
それでは上のm÷nの手順をプログラムにしてみましょう。
それが次です。
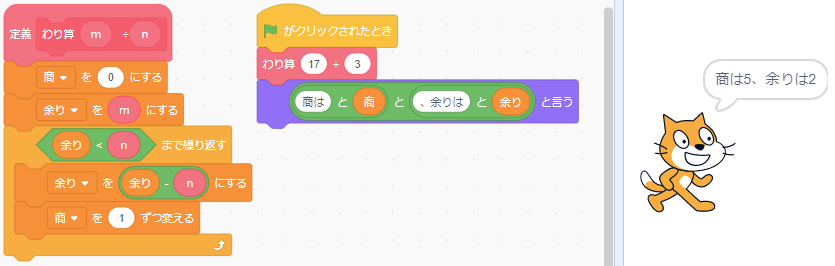
- 商(引けた回数)を0回に設定、余り(引き算の残り)をmに設定
- 余り に 余り―n を代入し、商に1をたす(引いた回数を数える)
これを 余り<n になるまで繰り返す - 商と余りを表示
「あまり」は文字通り「余りもの」だった!?
上の処理からわかるように、余りは文字通りの余りでね。
mからnを何度もひき算して、もうこれ以上はひき算できない。
けれども中途半端に数が残っている。
それが余りです。
「わり算」を「お茶くみ」の手順で考えれば、商が小数でも解ける!?
ところで、これまで「わり算」の意味を
m÷n=「mの中にnがいくつあるか?」
としていました。
しかし、m÷mの意味は、もう1つあります。
m÷n=「mをn当分したら、1つあたりいくつになるか?」
これは、お茶くみの手順で考えれば、解くことができます。
mミリリットルのお茶をn個のコップに入れていくと、1人あたり何ミリリットル?
mミリリットルを全て急須にいれて、n個のコップを並べます。
急須から少しずつn個のコップへお茶を注いでいき、均等になるようにしますよね。
そして、急須の中の量が少なくなるにつれて、分配するお茶の量も少なくしていきますよね。
最後の1周は1滴ずつとか(そこまでやらないか)。
この手順をプログラムにすればよいのです。
- まず、1ミリリットルずつ順番にn個のコップに入れていきます。
- そして、余りが1×nミリリットル未満になったら、今度は0.1ミリリットルずつ入れていきます。
- そして、余りが0.1×nミリリットル未満になったら、今度は0.01ミリリットルずつ入れていきます。
- そして、余りが0.01×nミリリットル未満になったら、今度は0.001ミリリットルずつ入れていきます。
・・・これを繰り返していき、最後に1つのコップに入っているお茶の量が商になります。
このようにすると、商が小数になるようなわり算でも「ひき算」の繰り返しで計算できることが分かるでしょう。
プログラミングは、みなさんの宿題にしたいと思います。
たし算の記号「+」と、かけ算の記号「×」が似ている理由
上で見たように、かけ算はたし算で計算できます。
そう考えると、かけ算の記号「×」と、たし算の「+」が似ているのも納得ですよね。
「+」を少しだけ変えて「×」が作られています。
というか、角度を45度かたむけただけですね。
似ているどころか、形は何も変わっていません。
よく考えられていますね。
ひき算の記号「-」と、わり算の記号「÷」が似ている理由
わり算は、ひき算の繰り返しでしたから、
わり算の記号「÷」と、ひき算の「-」が似ているのも納得です。
ただ、形も変わっています。
真ん中の横線は共通ですが、それに上下の「・」マークが追加されています。
これは「わり算」=「分数」だからでしょう。
m÷n=$ \frac{n}{m} $
と書けることは、小学5年生の算数の単元「等しい分数」で習います。
分数の形をデフォルメすれば、正に「÷」というピクトグラムになりますね。
よく考えられています。
わり算のもう1つの記号「/」
ところで、エクセルやプログラミングの計算式では、わり算の記号を「/」で表しています。
たし算の記号「+」を傾けて、かけ算の記号を「×」としたように、
ひき算の記号「-」を傾けて、わり算の記号を「/」とした方が、統一感があります。
グーグル検索で調べてみると、海外の学校や教科書では、むしろ「/」を採用している方が普通のようです。
さらにコロン「:」を使っている国もあるそうですよ。
なるほど、その手もありますね。
これからコンピューターの利用が進んでくると、わざわざキーボードにない「÷」を使うのはめんどうですね。
もしかしたら日本も将来は「/」になるのかもしれません。
ちなみにプログラミング言語 Pythonでは、
- m/n ・・・ m÷nの商(小数)
- m//n ・・・ m÷nの商(整数)
- m%n ・・・ m÷nの余り(整数)
という使い分けをしています。
コンピューターは「たし算」と「ひき算」しかできない!?
今から10年以上前に、塾長は趣味で望遠鏡を動かすプログラミングをしていました。
乾電池で動くような、とても小さなコンピューターを動かすプログラムでした。
このような小さなコンピューターは「マイコン」と呼ばれています。
マイコンにも色々ありますが、指先に載るような小さなものになると、使える命令がとても少ないです。
そのとき使っのは、PIC16Fなんちゃら、というマイコンでした。
それには四則計算の命令が「たし算」と「ひき算」の2つしかありませんでした。
「かけ算」と「わり算」が無いのです。
電卓を買ったら「×」と「÷」のボタンがなかった・・・というくらい衝撃でした。
「かけ算」や「わり算」が1回で計算できるコンピューターは高級品なのだと、そのとき知りました。
逆に、そのような高性能なコンピューターでも、中身は「たし算」と「ひき算」の組み合わせだけで作られているのだと実感しました。
考えてもみれば、これは当然です。
コンピューターはデジタルですから、0と1の数字をたくさん並べて計算しています。
0に1をたしたら1で、1から1を引いたら0です。
そのような処理を、膨大な数だけこなして、結果的にたくさん複雑な処理をしています。
だから究極的には、たし算とひき算しかしていません。
そう考えると今回は、
コンピューターの原理だけを使って「かけ算」や「わり算」をプログラミングした
とも言えます。
ちょっと大袈裟ですかね。
何はともあれ、計算には意味があります。
上のように「かけ算」や「わり算」の意味を深く理解してしまえば、文章題も怖くはありません。
あとがき
教科書が分かりやすくなり、一部はデジタル化しました。
無料で多くの分かりやすい解説動画が視聴できるようになりました。
分かりやすい教材があふれている今日ですが、だからといって、昔に比べて優秀な生徒が増えたという印象はありません。
つまり今も昔も、相変わらず
計算はできるけど文章題ができない
というのが、多くの生徒たちの悩みです。
計算の「やり方」はドリルで訓練しやすいです。
早く計算する「テクニック」も指導の良いネタです。
その一方で、
計算の「意味」や本質を考えさせるようなコンテンツは、なかなかウケません。
むしろ眠くなります。
しかし、それらにこだわって勉強しなければ、なかなか文章問題が得意にはならないでしょう。
そこが腕の見せどころ、と言ったところでしょうか。
きっとベテランの先生は、そういうのが得意なのだと思います。
ですから、より本質をつくようで、なおかつ面白くて飽きさせないようなコンテンツが、
きっとこれから先、どんどん登場してくることでしょう。
もしもプログラミングを活用した上のような事例が、その好例になるのなら幸いです。
生徒・保護者様のお友達登録はこちら
LINE登録するとプレゼントがもらえます!
【会員限定】お子様の成績と可能性を伸ばす18個のノウハウ
塾関係者様のお友達登録はこちら
LINE登録するとプレゼントがもらえます!
「zoomで簡単。オンライン授業移行の教科書」
または個別対談も可
名古屋市天白区の植田で塾を探すなら個別指導のヒーローズ!!
★ 直接のお問い合わせ ★
――――――――――――――――――――――
個別指導ヒーローズ 植田一本松校
〒468-0009
名古屋市天白区元植田1-202 金光ビル2F
TEL:052-893-9759
教室の様子(360度カメラ) http://urx.blue/HCgL