塾長です。
愛知県の公立高校受験。A日程が面接まで終わりました。そして明日からB日程。本日が学科試験に向けた最後の対策です。
中学2年生のキミたち。もう受験が始まっています。ぜひ今のうちに入試問題を見ておいて欲しいと思います。
中2までに習った範囲で、もう半分近く解けるはずなんだよ!
そこで、A日程の数学について、フル解説を作りました。考え方や発想法、何年生で解けるようになるかなど、できるだけ詳しく書きました。
ちょっとチャレンジしてみてね。
【1】次の(1)~(10)までの問に答えなさい。
(1)【中1】 $5-(-6)\div2$ を計算しなさい。
$5-(-6)\div2=5-(-3)=5+(+3)=8$
(2)【中2】 $\frac{3x-2}{4}-\frac{x-3}{6}$ を計算しなさい。
$\frac{3x-2}{4}-\frac{x-3}{6}$
$=\frac{(3x-2)\times3}{12}-\frac{(x-3)\times2}{12}$
$=\frac{9x-6-2x+6}{12}$
$=\frac{7x}{12}$
$(=\frac{7}{12}x)$
(3)【中3】 $\frac{3}{\sqrt{2}}-\frac{2}{\sqrt{8}}$ を計算しなさい。
$\frac{3}{\sqrt{2}}-\frac{2}{\sqrt{8}}$
$=\frac{3\times\sqrt{2}}{\sqrt{2}\times\sqrt{2}}-\frac{2}{2\sqrt{2}}$
$=\frac{3\sqrt{2}}{2}-\frac{\sqrt{2}}{\sqrt{2}\times\sqrt{2}}$
$=\frac{3\sqrt{2}}{2}-\frac{\sqrt{2}}{2}$
$=\frac{3\sqrt{2}-\sqrt{2}}{2}$
$=\frac{2\sqrt{2}}{2}$
$=\sqrt{2}$
(4)【中3】 $(2x+1)^{2}-(2x-1)(2x+3)$ を計算しなさい。
$(2x+1)^{2}-(2x-1)(2x+3)$
$=\{(2x)^2+2\times(2x)\times 1+1^{2}\}-\{(2x)^2+(-1+3)\times(2x)+(-1)\times(+3)\}$
$=\{4x^2+4x+1\}-\{4x^2+4x-3\}$
$=4x^2+4x+1-4x^2-4x+3$
$=4$
(5)【中3】 連続する3つの自然数を、それぞれ2乗して足すと$365$ であった。もとの3つの自然数のうち、もっとも小さい数を求めさい。
<解法1>
計算を楽にするため3つの自然数の真ん中を$n$とおく。
すると3つの自然数は$(n-1),\ n,\ (n+1)$とおける。
題意より方程式を立てて解けば、
$(n-1)^2+n^2+(n+1)^2=365,\ (n>0)$
$n^2-2n+1+n^2+n^2+2n+1=365,\ (n>0)$
$3n^2+2=365,\ (n>0)$
$3n^2=363,\ (n>0)$
$n^2=121,\ (n>0)$
$n=11$
よって、もっとも小さい数は$(n-1)$に代入して
$n-1=11-1$
$n=10$
である。<解法2>
素直に、問われている「もっとも小さい数」を$n$とおいた場合は次のようになる。
$n^2+(n+1)^2+(n+2)^2=365,\ (n>0)$
$n^2+n^2+2n+1+n^2+4n+4=365,\ (n>0)$
$3n^2+6n+5=365,\ (n>0)$
$3n^2+6n+5-365=0,\ (n>0)$
$3n^2+6n-360=0,\ (n>0)$
$n^2+2n-120=0,\ (n>0)$
$(n+12)(n-10)=0,\ (n>0)$
$n=10$
今回はこちらでも計算は難しくなかった。
(6)【中1】 次のア~エの中から$y$が$x$ の一次関数であるものをすべて選んで、そのかな符号を書きなさい。
ア 1辺の長さが$x\ cm$である立方体の体積$y\ cm^{3}$
イ 面積が$50\ cm^{2}$である長方形のたての長さ$x\ cm$と横の長さ$y\ cm$
ウ 半径が$x\ cm$である円の週の長さ$y\ cm$
エ $5\ \%$の食塩水$x\ g$に含まれる食塩の量$y\ g$
それぞれ$y$を$x$の式で表すと
ア $y=x^3$
イ $xy=50\ $より$\ y=\frac{50}{x}$(反比例)
ウ $y=2\pi x$(比例)
エ $y=\frac{5}{100}x$(比例)
である。
よって、一次関数の式$\ y=ax+b\ $または$\ y=ax\ (b=0\ のとき)\ $に当てはまるものは、
ウとエ
である。
(7)【中2】 5本のうち、あたりが2本はいっているくじがある。このくじをAさんが1本ひき、くじをもどさずにBさんが1本くじをひくとき、少なくとも1人はあたりをひく確率を求めなさい。
キーワード「少なくとも~」が出てきたら[1―逆の確率]が使えることが多いのだった。
そこで、
[少なくとも1人はあたりをひく]
の逆は
[1人もあたらない]=[2人とも外れる]
であることを考えて、[少なくとも1人はあたりを引く確率] = 1―[2人とも外れる確率]
を求めればよい。
そこで、まず
[2人とも外れる確率]
から求める。これは、
[1人目が5本のうちのハズレ3本のどれかをひき]なおかつ[2人目が残り4本のうちのハズレ2本のどちらかをひく]とき
の確率である。1人目がハズレを1本引いているので、2人目に残されたハズレは3-1=2本で、総数も5-1=4本になるからである(※)。
これを計算すると、
$\frac{3}{5}\times \frac{2}{4}=\frac{3\times 2}{5\times 4}=\frac{3\times 1}{5\times 2}=\frac{3}{10}$よって求める確率は、
$1-\frac{3}{10}$
$=\frac{10-3}{10}$
$=\frac{7}{10}$(※)もちろん樹形図を描けば明白です。
全部で20通りのうち、[2人とも外れる確率]は6通りだから、
[2人とも外れる確率]=$\frac{6}{20}=\frac{3}{10}$
(8)【中1】 $y$が$x$に反比例し、$x=\frac{4}{5}$のとき$y=15$である関数のグラフ上の点で、 $x$座標と$y$座標がともに正の整数となる点は何個あるか、求めなさい。
反比例 $\ y=\frac{a}{x}\ $の式より$\ xy=a\ $ だから $a=\frac{4}{5}\times15=4\times3=12\ $
よって、
$\ xy=12\ $
を満たす正の整数$x$と$y$の組$(x,y)$が何個あるかを考えれば良い。
12の約数で考えれば、$x=1,2,3,4,6,12\ $ と順番に考えれば、
$(x,y)=(1,12),\ (2,6),\ (3,4),\ (4,3),\ (6,2),\ (12,1)$
であるから6個。
(9)【中2】 2直線$\ y=3x-5,\ y=-2x+5\ $ の交点の座標を求めなさい。
2つの式を連立方程式で解く。代入法により、
$3x-5=-2x+5$
$3x=-2x+5+5$
$3x+2x=10$
$5x=10$
$x=2$
これを$\ y=3x-5\ $に代入して($\ y=-2x+5\ $ に代入しても、どちらでも良い)
$y=3\times2-5=1$
よって答えは
$(2,\ 1)$
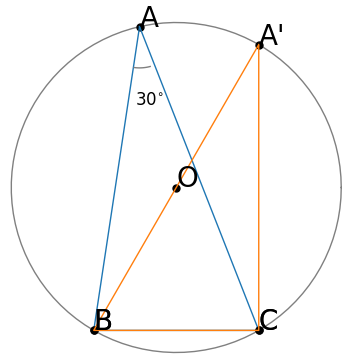
(10)【中3】 図で、A,B,Cは円Oの周上の点である。円Oの半径が$6\ cm$、∠BAC$=30^{\circ}\ $のとき、線分BCの長さは何$cm$か、求めなさい。
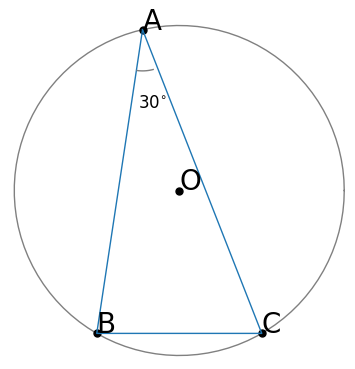
<解法1>
「Aが円周上」→「円周角の定理を使う」と着想する。
さらに、
「半径が$6cm$」→「半径$6cm$または直径$12cm$を使ってBCを求める」と着想する。
さらにここから「直径に対する円周角は$90^{\circ}\ $ 」という性質も連想する。
以上の発想から次のように⊿A’BCを作図する。
円周角の定理より、∠BAC=∠BA’C=$30^{\circ}\ $ かつ ∠BCA’=$90^{\circ}\ $ である。
よって三平方の定理から$BC:A’B=1:2$とわかる。
これは三角定規でお馴染みの$30^{\circ}、60^{\circ}、90^{\circ}\ $の直角三角形だから、辺の比は既知である。
よって、
$1:2=BC:12$
$2\times BC=1\times12$
$BC=6$
より
$BC=6cm$
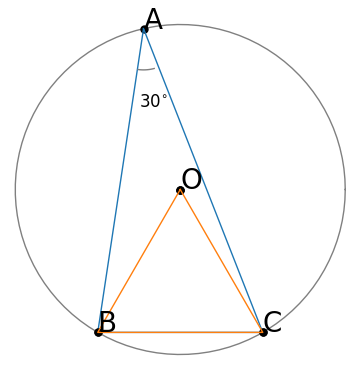
<解法2>
「Aが円周上」→「円周角の定理を使う」→「中心角」を連想する。
そこでOからB、Cに半径を引く。
円周角の定理「中心角=円周角×2」から、
∠BOC=$30^{\circ}\times 2=60^{\circ}\ $
さらにOB=OCから二等辺三角形の性質「底角が等しい」をつかって、
∠OBC=∠OCB=$\{180^{\circ}-60^{\circ}\}\div 2=60^{\circ}\ $
よって$\triangle OBC\ $は正三角形となるので、
OB=OC=BC
つまり、
$BC=6cm$
【2】次の(1)~(3)までの問に答えなさい。
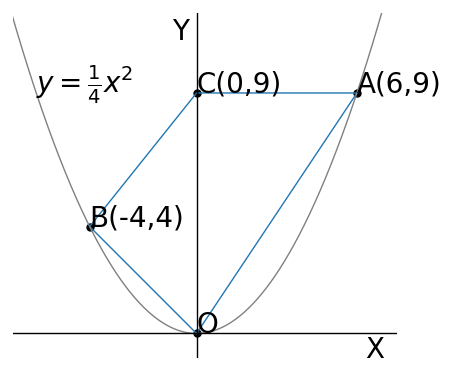
(1)【中3】 図で、Oは減点、A,Bは関数$\ y=\frac{1}{4}x^2\ $ のグラフ上の点で、点Aの$x$座標を正、$y$座標は9、点Bの$x$座標は―4である。また、Cは$y$軸上の点で、直線CAは$x$軸とへいこうである。
点Cを通り、四角形CBOAの面積を二等分する直線の式を求めなさい。
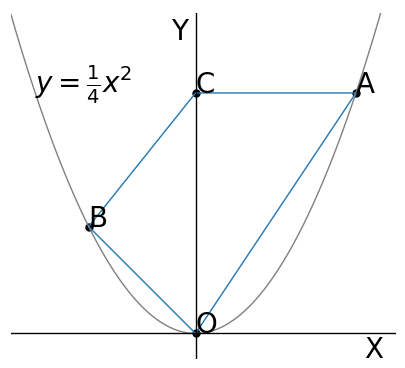
まず題意より各点の座標を求めて書き込むと次のようになる。
ここで題意の「点Cを通り、四角形CBOAの面積を二等分する直線」が辺OBを通るのか、辺OAを通るのかを知る必要がある。
そこで⊿OCBと⊿OACの面積を求めて比較すれば、大きい面積の方を通ると分かる。どちらもOCを底辺と考えれば、
$\triangle OCB=\frac{1}{2}\times9\times4=18$
$\triangle OAC=\frac{1}{2}\times9\times6=27$
よって、求める直線は⊿OACを通るため、辺OAと交わる。
その交点をEとし、その$x$座標を$t$としておく。直線OAの式は、原点を通り、傾き=$\frac{9}{6}=\frac{3}{2}$である比例の式だから、
$直線OA: \ y=\frac{3}{2}x\ $である。
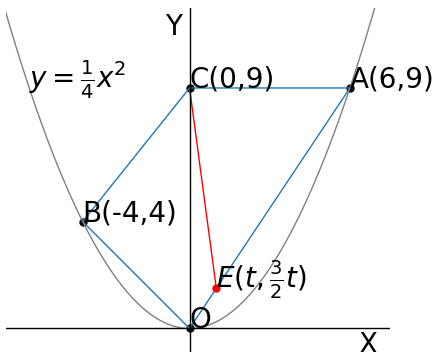
よって交点Eの座標は$\ (t, \frac{3}{2}t)\ $である。これを図示すれば、次のようになる。
直線CEは四角形CBOAの面積を二等分するから、次の等式となる。
$\triangle OCB+\triangle OCE=\triangle OAB-\triangle OCE$
ここで
$\triangle OCE=\frac{1}{2}\times 9\times t=\frac{9t}{2}$
だから、
$18+\frac{9t}{2}=27-\frac{9t}{2}$
これを解いて、
$\frac{9t}{2}+\frac{9t}{2}=27-18$
$9t=9$
$t=1$
よって点Eは、$\ (t, \frac{3}{2}t)=(1, \frac{3}{2})\ $である。最後に、直線CEの式 $\ y=ax+b\ $ の$\ a,\ b\ $を求める。
切片$\ b\ $は9である。
$C(0,9)→E(1,\frac{3}{2})$での変化の割合$\ a\ $は、教科書にある定義どおりに式を立てると、
$$a=\frac{\{ \frac{3}{2} – 9\} }{\{1-0\}}$$
という複雑な式になるが、分母は1なので分子だけ計算すればよい。
$a=\frac{3}{2} – 9 $
$=\frac{3}{2}-\frac{18}{2}$
$=\frac{-15}{2}$以上から、
$$y=-\frac{15}{2}x+9$$
―――【参考】―――
もしも
$$\frac{分数}{分数}=\frac{\frac{a}{b}}{\frac{c}{d}}$$
となってしまったら?分数の中に分数が出てきたら困ってしまいますね。そういうときは
$\frac{A}{B}=A\div B$
を思い出しましょう。
$A=\frac{a}{b},\ B=\frac{c}{d}$ と考えれば、
$\frac{分数}{分数}$
$=\frac{\frac{a}{b}}{\frac{c}{d}}$
$=\frac{A}{B}$
$=A\div B$
$=\frac{a}{b}\div \frac{c}{d}$
$=\frac{a}{b}\times \frac{d}{c}$
$=\frac{a\times d}{b\times c}$
$=\frac{ad}{bc}$とすればよいです。つまり
「分母の分数を逆数にしてかける」
と考えればよいです。
(2)【中1】 次の文章は、体育の授業でサッカーのペナルティキックの練習を行ったときの、1人の生徒がシュートを入れた本数とそれぞれの人数について述べたものである。
文章中の【A】にあてはまる式を書きなさい。また、【a】、【b】、【c】にあてはまる自然数をそれぞれ書きなさい。
なお、3か所の【A】には、同じ式があてはまる。
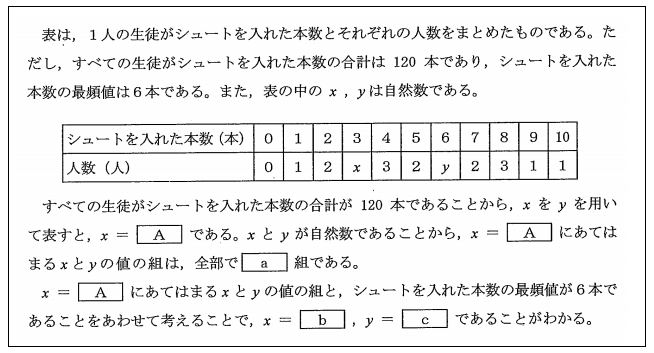
この問題文の日本語には少し難があるが、シュートに1回成功した人が1人、2回成功した人が2人・・・5回成功した2人・・・などと調査したという意味である。
つまりシュートに成功した回数について、何人が成功したかを度数とする度数分布表になっている。まず【A】について考える。
題意より「シュートすべての合計=120」という式を立てればよい。よって
$0\times 0+1\times 1+2\times 2+3\times x+4\times 3+5\times 2+6\times y+7\times 2+8\times 3+9\times 1+10\times 1=120$
$0+1+4+3x+12+10+6y+14+24+9+10=120$
$84+3x+6y=120$
$3x=-6y+120-84$
$3x=-6y+36$
$x=-2y+12$ここで$\ x>0,\ y>0\ $であるから、この式を見ながら$\ y=1,\ 2,\dots\ $と代入していけば、$\ x\ $と$\ y\ $の組合わせは、
$\ (x,y)=(10,1),\ (8,2),\ (6,3),\ (4,4),\ (2,5)\ $
である。よって
【a】は「5」組となる。しかし、題意の「最頻値は6本」を満たすためには、
$\ y>3\ $かつ$\ y>x\ $
でなければならない。これを満たす組合わせは、
$\ (x,y)=(2,5)\ $
だけである。よって
【b】は「2」
【c】は「5」
(3)【中2】 図のような池の周りに1周$\ 300\ m\ $ の道がある。
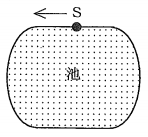
Aさんは、S地点からスタートし、矢印の向きに道を5周走った。1周目、2周目は続けて毎分$\ 150\ m\ $で走り、S地点で止まって3分間休んだ。休んだ後すぐに、3周目、4周目、5周目は続けて$\ 100\ m\ $で走り、S地点で走り終わった。
Bさんは、AさんがS地点からスタートして9分後に、S地点からスタートし、矢印の向きに道を自転車で1周目から5周目まで続けて一定の速さで走り、Aさんが走り終わる1分前に道を5周走り終わった。
このとき、次の①、②の問いに答えなさい。
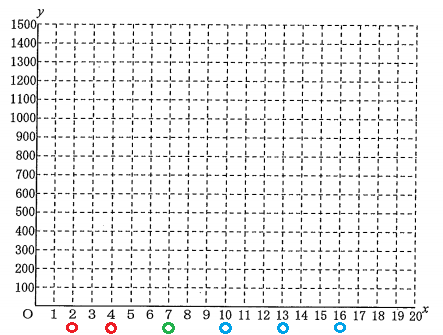
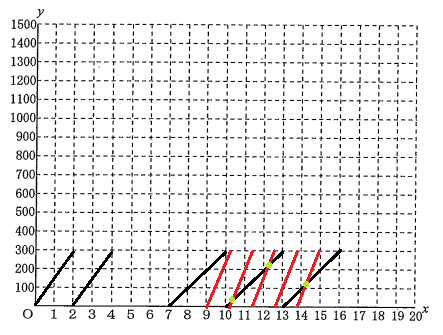
① Aさんがスタートしてから$\ x\ $分間に走った道のりを$\ y\ m\ $とする。AさんがスタートしてからS地点で走り終わるまでの$\ x\ $と$\ y\ $の関係を、グラフに表しなさい。
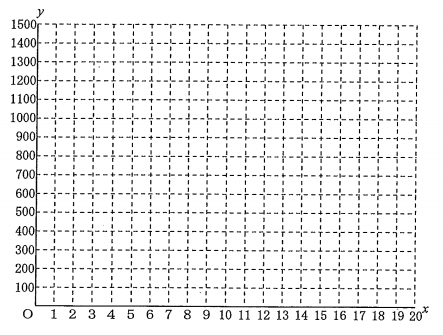
まずAさんが行った順に、時間の経過を計算する。
1周目と2周目は、それぞれ$\ 300\div150=2\ $分であり、2周の合計は4分間。つまり最初の0分~4分の間はこのペース。
次に3分の休憩を取ったので、4~7分は距離が変わっていない。
その後3周目から5周目までは、それぞれ$\ 300\div100=3\ $分であり、3周の合計は9分間。つまり7分~16分の間はこのペース。
以上の時間の流れを図に色分けして書きこむと次のようになる。
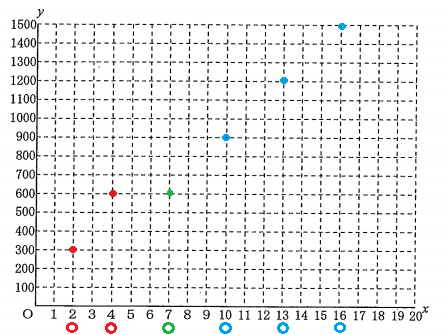
そして1周$\ 300\ m\ $と決まっているので、マークからマークの間は必ず$\ y\ $は$\ 300\ $ずつ増えていく。
ただし休憩の間は$\ y\ $が変わらず、水平線になる。
これらに注意して、次のように印をつけることができる。
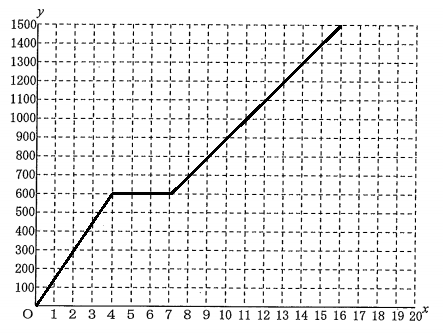
最後に、これらの点を線で結べばグラフが完成する。
② BさんがAさんを追い抜いたのは何回か、答えなさい。
Bさんが走り始めた9分目のとき、Aさんは残り3周あった(2周しか完走していなかった)。
2人が一緒に走っていた時間帯は、9分目~15分目までである。
Bさんの方が早く完走したので、Bさんは、Aさんが残り3周を走る様子をすべて目撃できたことになる。
よって追い抜いた回数は3回と分かる。直感的にはこれで解答できるが、もう少しグラフで考える。
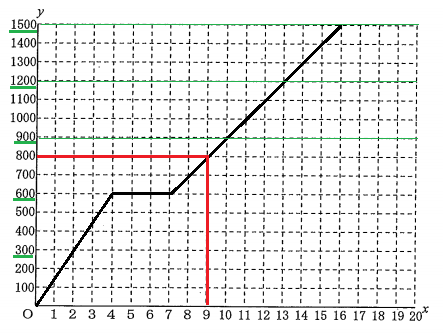
上のグラフは$\ y\ $軸が「走った合計」の距離になっているので分かりにくい。
Aさん、Bさんのそれぞれが「何分後に何周目の何メートル地点を走っているのか」を分かりやすく表示するためには、1周$\ 300\ m\ $を走るごとに、距離($\ y\ $)を0メートに戻すようなグラフを描くべきである。具体的には次のようになる。
黒い線がAさんが走った様子であり、赤い線がBさんが走った様子である。黄緑の点が交点、つまり追い抜いた点である。
よってBさんはAさんを3回追い抜いた。
【3】次の(1)~(3)までの問に答えなさい。
ただし、答えは根号をつけたままでよい。
(1)【中2】 図で、Dは$\triangle ABC$の辺AB上の点で、DB=DCであり、Eは辺BC上の点、Fは線分AEとDCとの交点である。
∠DBE=$47^{\circ}\ $、∠DAF=$31^{\circ}\ $のとき、∠EFCの大きさは何度か、求めなさい。
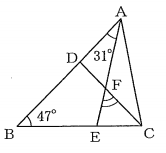
DB=DCより二等辺三角形の性質により、∠DBC=∠BCD=$47^{\circ}\ $。
また外角の公式から、∠ADC=∠DBC+∠BCD=$47^{\circ}+47^{\circ}=94^{\circ}\ $。
よって、∠EFC=$180^{\circ}-(94^{\circ}+31^{\circ})=180^{\circ}-125^{\circ}=55^{\circ}$
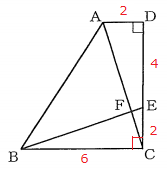
(2)【中3】 図で、四角形ABCDは、AD//BC、∠ADC=$90^{\circ}\ $の台形である。Eは辺DC上の点で、$DE:EC=2:1\ $であり、Fは線分ACとEBとの交点である。
$AD=2\ cm$、$BC=DC=6\ cm$のとき、次の①、②の問に答えなさい。
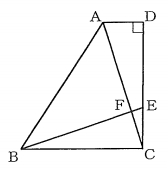
①【中3】 線分EBの長さは何$cm\ $か、求めなさい。
題意から分かる長さや角度を書き込むと下図のようにいなる。
三平方の定理から
$EB=\sqrt{6^2+2^2}=\sqrt{36+4}=\sqrt{40}=2\sqrt{10}$
よって
$2\sqrt{10}\ cm$
②【中3】 $\triangle ABF$の面積は何$cm^2\ $か、求めなさい。
$\triangle ABF=\triangle ABC-\triangle FBC$ で計算する方針でいこう。
すると$\triangle CEF$の面積を求める必要があるので、それを出しておく。そのために$\triangle CEF$∽$\triangle BEC$ を示す。
まず、$\triangle ACD\equiv\triangle EBC$
よって、∠EBC=∠ACD$\triangle CEF$と$\triangle BEC$について、
∠EBC=∠ACD
また共通の角だから、
∠CEF=∠BEC
2角が等しいので、
$\triangle CEF$∽$\triangle BEC$相似比から、
$EB:EC=2\sqrt{10}:2=2:EF$
$2\sqrt{10}EF=4$
$EF=\frac{4}{2\sqrt{10}}=\frac{2}{\sqrt{10}}=\frac{2\sqrt{10}}{10}=\frac{\sqrt{10}}{5}$
よって、
$EF:EB=2\sqrt{10}:\frac{\sqrt{10}}{5}=2:\frac{1}{5}=10:1$
よって、
$\triangle FBC=\frac{9}{10}\triangle EBC=\frac{9}{10}\times \frac{1}{2}\times 6\times 2 = \frac{27}{5}$
以上から、
$\triangle ABF=\triangle ABC-\triangle FBC=\frac{1}{2}\times 6\times 6 – \frac{27}{5}=18-\frac{27}{5}=\frac{18\times5-27}{5}=\frac{90-27}{5}=\frac{63}{5}$
よって、
$\frac{63}{5}\ cm^2$
(3)【中1・中3】 図で、Dは$\triangle ABC$の辺BC上の点で、$BD:DC=3:2\ $、AD⊥BCであり、Eは線分AD上の点である。
$\triangle ABE$の面積が$\triangle ABC$の面積の$\frac{9}{35}$倍であるとき、次の①、②の問に答えなさい。
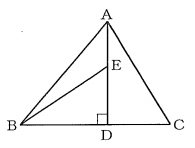
①【中1】 線分AEの長さは線分ADの長さの何倍か、求めなさい。
$BD:DC=3:2\ $より、$\triangle ABD$は$\triangle ABC$の$\frac{3}{5}$倍である。
よって、線分AEの長さは線分ADの長さの$\ x\ $倍だとすると、
$\triangle ABC\times\frac{9}{35}=\triangle ABC\times\frac{3}{5}x$
よって、
$\frac{9}{35}=\frac{3}{5}x$
であるから、これを解いて
$x=\frac{3}{7}$倍
②【中3】 $\triangle ABE$を、線分ADを回転の軸として1回転させてできる立体の体積は、$\triangle ADC$を、線分ADを回転の軸として1回転させてできる立体の体積の何倍か、求めなさい。
まず回転してできる円錐の底面の半径は$\frac{3}{2}$倍であるから、底面積は$\frac{9}{4}$倍である。
そして高さは$\frac{3}{7}$倍であるから、合わせて、
$\frac{9}{4}\times \frac{3}{7}$
これを計算して
$\frac{27}{28}$倍
あとがき
毎年の難易度に比べれば、全体的には標準的な内容でした。
高得点を狙う受験生にとっては、つぎの問題が合格点の分かれ目になったかもしれません。
大問1-(2)の問題は、作業ミスを誘発しやすかったかもしれません。多くの人が「xを代入してyを求める」手順に慣れていると思います。しかし【a】では逆に「yからxを求める」手順に逆転していました。人によっては情報を整理する過程で、xとyを逆に書くという作業ミスを誘発しやすい問題でした。【b】は「最頻値」からxやyの変域や大小関係を思いつけたか否かがポイントになったことでしょう。
大問2―(3)―②の問題は「1回」と誤答した人が多かったかもしれません。単純にBさんのグラフを書き込むと交点が1つしか見つけられなかったので違和感を覚えて困った人も多かったのではないでしょうか。
大問3―(2)―②の問題は、直感的に方針が立ちにくいです。大局的に計算の方針を定めて、逆算して細かな計算を行うという「作業の段取り」を意識することが大切でした。
大問3―(3)―②の問題は、立体の「高さ」の本質を理解していなければ、①の答えが②で「高さの倍率」として使えることを思いつけなかったかもしれません。小学生で三角形の面積が高さに比例することを色々とやりましたが、その感覚があれば思いついたのかもしれませんね。
余談ですが、
大問2―(2)の問題は、日本語がおかしいです。ちょっと出題ミスにギリギリ近い日本語の崩壊。すぐに度数分布だと分かった人は良いですが、読解力のある人ほど混乱したかもしれません。コロナ禍で出題の方針が急変更され、問題作成の現場はとても混乱していた様子がうかがえます。
解説に登場したグラフや図、数式の表示について
図やグラフについて
前半の円や二次関数のグラフはプログラミングで作成しました。
後半の図は公開されている問題をスキャンした画像と、それを2次加工した画像です。
数式について
数式はパソコンで入力するのが難しいですよね。
このブログでは$\TeX$(「テフ」と読みます)という、数式専用の言語を使って数式を書いています。だから数式がキレイに表示できます。
これもプログラミングみたいなものです。
$\TeX$は理系の大学生がレポートや論文を書くときに便利です。
理系の大学生は知っておくと便利です。
高校生でもバカロレアDPコースの生徒たちなど、レポート提出の多い人には便利だと思いますよ。
興味のある方は調べてみてください。
図やグラフはプログラミングで作成
大問1(10)および大問2(1)のグラフや図を作るのにつかったプログラムは以下です。
プログラミング言語はPython(パイソン)です。
残念ながら中学生では理解するのがとても難しいです。高校の数学を使います。
なお、パイソンのプログラミングは、プログラミング教室「マイクラミング」の「プロコース」で開講しています。
小学生から大学生まで受講しています。興味のある人は、お問い合わせくださいませ。
---------------------
import random as rd
import time as tm
import numpy as np
import matplotlib.pyplot as plt
import math
def initGraph(title="graph", xLabel="x", xMin=-1.0, xMax=1.0, yLabel="y", yMin=-1.0, yMax=1.0, N=100):
fig = plt.figure(figsize=(5,5), dpi=N)
axs = fig.add_subplot(1, 1, 1)
plt.title(title)
plt.xlabel(xLabel)
plt.ylabel(yLabel)
plt.xlim(xMin, xMax)
plt.ylim(yMin, yMax)
plt.gca().spines['right'].set_visible(False)
plt.gca().spines['top'].set_visible(False)
# plt.xticks(fontsize=20)
# plt.yticks(fontsize=20)
axs.set_aspect(1)
return axs
def addDot(axs, x, y, text=True, arg="", c="black", fs=5):
axs.plot(x, y, '.', markersize=10, c=c)
if text:
if arg != "":
plt.text(x, y ,arg, fontsize=fs)
else:
plt.text(x,y," ({}, {})".format(x,y), fontsize=fs)
def addDots(axs, x, y, args="", line=True, fs=5):
c=0
xs = []
ys = []
for t in x:
xs.append(x[c])
ys.append(y[c])
if args!="":
addDot(axs, x[c], y[c], text=True, arg=args[c], fs=fs)
else:
addDot(axs, x[c], y[c], text=False)
c+=1
if line:
xs.append(xs[0])
ys.append(ys[0])
axs.plot(xs, ys, linewidth=1)
def addLines(axs, x, y, c="black", tx=0.0, ty=0.0, text="", fs=5):
axs.plot(x, y, linewidth=1, c=c)
if text!="":
plt.text(tx,ty,text, fontsize=fs)
def addCircle(axs, x=0.0, y=0.0, r=1.0, s=0, e=2*np.pi, c="black"):
theta = np.linspace(s, e, 100)
xs = x + r*np.cos(theta)
ys = y + r*np.sin(theta)
axs.plot(xs, ys, linewidth=1, c=c)
def addDotsOnCircle(axs, r, thetas, args, line=True, fs=5):
c=0
xs = []
ys = []
for t in thetas:
x=r*math.cos(t)
y=r*math.sin(t)
xs.append(x)
ys.append(y)
addDot(axs, x, y, text=True, arg=args[c], fs=fs)
c+=1
if line:
xs.append(xs[0])
ys.append(ys[0])
axs.plot(xs, ys, linewidth=1)
def showGraph(arrows=True, grid=True):
if arrows:
#x軸
plt.axhline(0, linewidth=1, color="black")
#y軸
plt.axvline(0, linewidth=1, color="black")
if grid:
#方眼線(グリッド線)
plt.grid(True)
plt.show()
def Toi1_10():
A_theta = 4*math.pi/7
B_theta = 4*math.pi/3
C_theta = 5*math.pi/3
AD_theta = math.pi/3
Radis = 6.0
axs=initGraph(xMin=-7.0, xMax=7.0, yMin=-7.0, yMax=7.0)
addDot(axs,0.0,0.0,True,"O", fs=20)
addCircle(axs, r=Radis, c="gray")
addDotsOnCircle(axs, r=Radis, thetas=[A_theta, B_theta, C_theta], args=['A','B','C'], fs=20)
addCircle(axs, x=Radis*math.cos(A_theta), y=Radis*math.sin(A_theta), r=1.5, s=((A_theta+B_theta+math.pi)/2), e=((A_theta+C_theta+math.pi)/2), c="gray")
plt.text(-1.5, 3.0, r"$30^{\circ}$", fontsize=12)
# addDotsOnCircle(axs, r=6.0, thetas=[AD_theta, B_theta, C_theta], args=['A\'','B','C'], fs=20)
addDots(axs, x=[0.0, Radis*math.cos(B_theta), Radis*math.cos(C_theta), 0.0], y=[0.0, Radis*math.sin(B_theta), Radis*math.sin(C_theta), 0.0], line=True)
showGraph(arrows=False, grid=False)
def Toi2_1():
axs=initGraph(xMin=-7.0, xMax=7.5, yMin=-1.0, yMax=12.0)
plt.text(6.3,-0.9,"X", fontsize=20)
plt.text(-0.9,11.0,"Y", fontsize=20)
# addDots(axs, x=[0.0, 6.0, 0.0, -4.0], y=[0.0, 9.0, 9.0, 4.0], args=['O','A','C','B'], line=True, fs=20)
addDots(axs, x=[0.0, 6.0, 0.0, -4.0], y=[0.0, 9.0, 9.0, 4.0], args=['O','A(6,9)','C(0,9)','B(-4,4)'], line=True, fs=20)
x = np.arange(-7.0, 7.0, 0.01)
y = x*x/4
addLines(axs,x,y,"gray", -6.0, 9.0, r"$y=\frac{1}{4}x^{2}$", fs=20)
addDot(axs, 1.0, 1.5, text=True, arg=r"$E(t,\frac{3}{2}t)$", c="red", fs=20)
addLines(axs,x=[0.0,1.0],y=[9.0,1.5],c="red", fs=20)
showGraph(arrows=True, grid=False)
if __name__ == "__main__":
Toi1_10()
# Toi2_1()
---------------------
※プログラムで難しいところ
三角関数($sin\theta,\ cos\theta$)や極座標を使っていますので、高校の数学です。円O上の点A,B,Cの座標を、円の半径 Radisと、x軸とOA、OB、OCのなす角、A_theta、B_theta、C_theta を使って求めています。その計算に三角関数を使います。
また∠BACを図示するために、円周上の点Aを中心に弧を描いています。点Aから見た、x軸方向とAB、ACのなす角を、A_theta、B_theta、C_theta を使って求める必要があります。この計算をするために、プログラミングする前に紙面上で幾何学の問題を解く必要がありました。
進学実績
卒塾生(進路が確定するまで在籍していた生徒)が入学した学校の一覧です。
ちなみに合格実績だけであれば更に多岐・多数にわたりますが、当塾の理念に反するので生徒が入学しなかった学校名は公開しておりません。
国公立大学
名古屋大学、千葉大学、滋賀大学、愛知県立大学、鹿児島大学
私立大学
中央大学、南山大学、名城大学、中京大学、中部大学、愛知淑徳大学、椙山女学園大学、愛知大学、愛知学院大学、愛知東邦大学、同朋大学、帝京大学、藤田保健衛生大学、日本福祉大学
公立高校
菊里高校、名東高校、昭和高校、松陰高校、天白高校、名古屋西高校、熱田高校、緑高校、日進西高校、豊明高校、東郷高校、山田高校、鳴海高校、三好高校、惟信高校、日進高校、守山高校、愛知総合工科高校、愛知商業高校、名古屋商業高校、若宮商業高校、名古屋市工芸高校、桜台高校、名南工業高校
私立高校
中京大中京高校、愛工大名電高校、星城高校、東邦高校、桜花学園高校、東海学園高校、名経高蔵高校、栄徳高校、名古屋女子高校、中部第一高校、名古屋大谷高校、至学館高校、聖カピタニオ高校、享栄高校、菊華高校、黎明高校、愛知みずほ高校、豊田大谷高校、杜若高校、大同高校、愛産大工業高校、愛知工業高校、名古屋工業高校、黎明高校、岡崎城西高校、大垣日大高校
(番外編)学年1位または成績優秀者を輩出した高校
天白高校、日進西高校、愛工大名電高校、名古屋大谷高校
※ 成績優秀者・・・成績が学年トップクラスで、なおかつ卒業生代表などに選ばれた生徒
生徒・保護者様のお友達登録はこちら
LINE登録するとプレゼントがもらえます!
【会員限定】お子様の成績と可能性を伸ばす18個のノウハウ
塾関係者様のお友達登録はこちら
LINE登録するとプレゼントがもらえます!
「zoomで簡単。オンライン授業移行の教科書」
または個別対談も可
名古屋市天白区の植田で塾を探すなら個別指導のヒーローズ!!
★ 直接のお問い合わせ ★
――――――――――――――――――――――
個別指導ヒーローズ 植田一本松校
〒468-0009
名古屋市天白区元植田1-202 金光ビル2F
TEL:052-893-9759
教室の様子(360度カメラ) http://urx.blue/HCgL