塾長です。
受験生のみなさん、受験勉強お疲れさまでした。
さて、卒業も受験も終え、きっと今は時間を持て余していることでしょう。
教室では早くも高校の予習を始めておりますが、プライベートではいかがでしょう?
新型コロナの蔓延防止や花粉症で外出を控えているのであれば、読書やコンピューターがおすすめですよ。
ネットをやるなら、情報リテラシーを意識しましょう。
そこで今回は、情報リテラシーとプログラミングの関係について、1つの例を書いてみましょう。
情報リテラシーと数学の関係
最近、ちょっと話題になった有名な話があります。
次のニュースを見たとき、あなたならワクチンの効果をどう評価しますか?
問1:効果なし?
ウィルスに新規感染した人の約6割がワクチンを2回接種していたことが判明。
この調査から、ワクチンの効果が無いと判断するのは正しいでしょうか?
ソース:「オミクロン株感染で入院の6割は2回接種済み 国立感染研の分析で判明」Science Portal(2022/02/01)など
もう1つの事例です。こちらは、ここ数日間で話題に上ってきました。
問2:逆も言える?
東大の鳥海教授がツイッターの投稿をクラスター分析したところ、次のことが判明。
ロシアのウクライナ侵攻を正当化する主張「ウクライナ政府はネオナチ政権だ」などを拡散している人たちの88%は、ワクチン接種に反対する投稿も拡散していた。それでは逆に、ワクチン接種に反対する人の多くは、ロシアの主張を拡散している人だと言えるでしょうか?
ソース:「ツイッター上でウクライナ政府をネオナチ政権だと拡散しているのは誰か」YHAHOO!ニュース(2022/3/7)
このようなニュースは毎日のようにネット上に流れていますが、よく考えないと勘違いを起こしてしまいます。
もしかしたら印象操作に載せられてしまうリスクさえあります。
それでは答え合わせです。
答え
問1
ワクチンの効果はあったと言える。
この種のニュースの秘密は、ワクチンを「接種した人」と「接種していない人」の人数比にあります。
ワクチンの2回接種まで完了した人の割合は、日本の総人口の79%を上回っています。
対象者約1億2千700万人のうち、約1億人が2回接種済みで、残り2千700万人がそれ未満の接種です。
ソース:「チャートで見る日本の接種状況 コロナワクチン」日本経済新聞や首相官邸の発表など)。
例えば問1のニュースの例では、オミクロン株の新規感染者122人が対象でした(昨年の感染者はまだ少なかったです)。
うち77人が2回接種済みで、40人が未接種、他は3回接種や1回接種だったそうです。
これを母数も合わせてみれば、
接種済みの感染率 77÷1億=0.000077%
未接種での感染率 40÷2700万=0.0001481%
両者を割れば、未接種の人の方が1.9倍も感染していることになりました。
あくまでも当時での数字でしかありませんが、少なくとも当時はワクチン接種で感染リスクが半減していたと言えます。
問2
逆は言えない。ワクチン接種に反対していることとウクライナ戦争の話はもともと関係ない。
何より上のソース記事を最後までよく読めば、ちゃんと「ワクチン接種に反対する人のわずか4%」と書かれています。
これについては後で計算してみますが、何はともあれ、よく読むことが大切ですね。
もしも書かれていない場合は、別の情報ソースなども合わせて、ちゃんと母集団の数や相対度数などを確かめる必要があります。
ちなみに、この種の問題は小学6年生の3学期「なかまに分けて」で習います。
あるいは、高校1年生の数1「集合と論理」でも習います。
いわゆる「りんごが好きな人」「みかんが好きな人」「両方とも好きな人」の問題です。
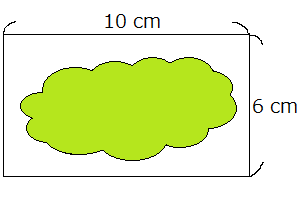
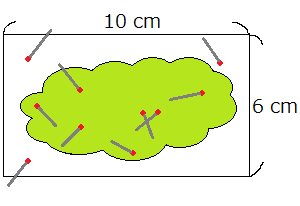
「りんごが好きな人」は40人で、「みかんが好きな人」は80人でした。
このとき「りんごが好きな人」の約88%はみかんも好きでした。
さて「みかんが好きな人」はりんごも好きだと言えるでしょうか?40人の88%=35人ですから「両方とも好きな人」が35人です。
つまり「みかんが好きな人」の80人のうち35人がリンゴも好きということになり、半数未満でした。
よって、「みかんが好きな人」はりんごも好きだとは言えません。
このような話しと同じですね。
そもそも、この分析は
「特定の主張が特定の集団によって、繰り返し意図的に拡散されているのではないかないか?」
という疑いをデータ分析の観点から明らかにしようという試みでした。
このソース記事の中では、
Dクラスタは「ウクライナ政府はネオナチである」というロシアの主張を拡散しているツイート群で,228ツイートが10,907アカウントによって30,342回拡散していました.(中略)クラスタDだけ2.8と大きいようです
という分析もされています。
つまり、特定の集団が「ウクライナ政府はネオナチである」という同様のツイートを1人当たり平均2.8回も繰り返し拡散していたことになります。
これは「意図的な拡散」であったと言えるでしょう。
とても興味深いですね。
ですが、こんな素敵な調査でも、その読み方や解釈を間違えてしまったら、自分も意図せず陰謀論を担いでいる側になってしまいます。
話がそれましたが、今回は「逆は成り立たない」が正解でした。
ワクチンを接種しない自由も認められています。
ワクチンを接種するか否かという選択の話と、陰謀論でワクチンを反対している人の話は、別の話です。
両者は分けてとらえるべきでしょう。
このように情報は気を付けて読む必要がありますね。
ところで、算数や数学に置き換えることができるということは、プログラミングでも話ができます。
数学ならばプログラミングにできる
数学の式で関係を表す
そこで問2の話題について、数学の集合で表してみましょう。
$N=${ロシアの主張を拡散する人の集合}(ロシアによるウクライナ侵攻を正当化する人)
$V=${ワクチン接種に反対する人の集合}
すると
$N \cap V=${ロシアの主張を拡散し、かつ、ワクチン接種に反対する人の集合}
$ V – (N \cap V) =${ワクチン接種に反対する人の中で、ロシアの主張を拡散する人の集合}
などと表せますから、$V$ と $N \cap V $ を比較すれば良いということになります。
ここから数学の慣例で、集合の要素の数を$n(集合)$と表すことにします。
あくまでも今回は思考の練習ですから、値は適当にデフォルメします。
いま、適当に $n(N)=10$とします。
本当の数は10,907アカウントですが、面倒なので全体的に $ \frac{1}{1000} $ 程度に規模を縮小しました。
すると $n( N \cap V )$ はその88%ですから、$n( N \cap V )=10 \times 0.88 \risingdotseq 9$ と設定すればよいでしょう。
さらに、その9人は $V$の4%ですから、$n(V) = n(N \cap V) \div 0.04 = 225$ と設定します。
これで練習用の数字がそろいました。
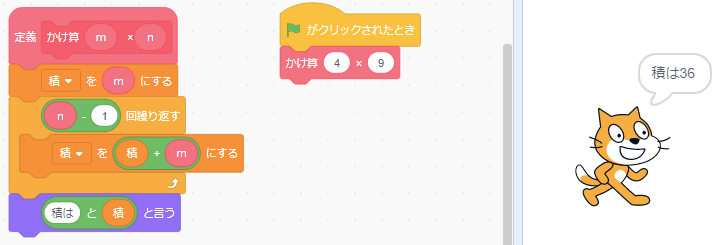
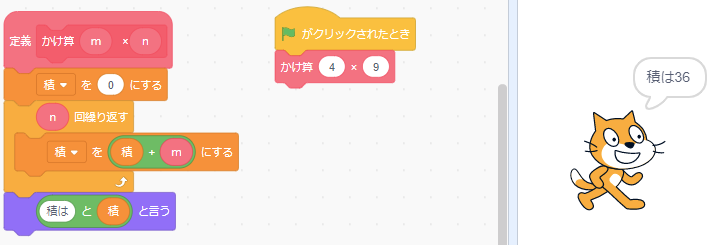
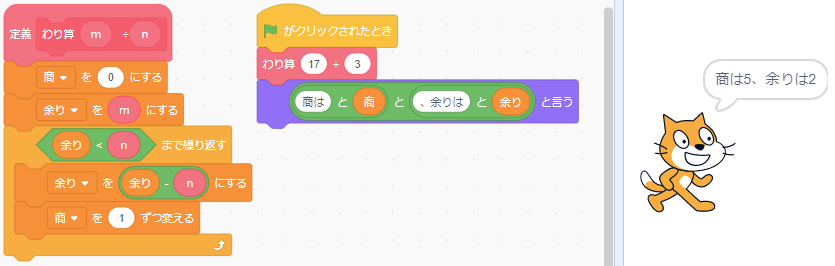
プログラミングで表現する
それでは、上記の関係をプログラミングで実験してみましょう。
なおプログラミング言語は Python(パイソン)を使います。
Python は無料で使えるプログラミング言語です。人気ランキングで上位にいることでも有名です。
使ってみたい方は、Pythonの公式ホームページからダウンロードしてインストールしてみてください。
さて、Python は集合の計算もプログラミングできます。
Python では $n(U)$ を $len(U)$ とし、$N \cap V$ を $N \& V$ と書きます。
それでは集合Nや集合Vを具体的に定義していきましょう。
本当なら集合の要素はツイッターのアカウント名なのですが、プログラミングの都合で、今回は簡易的に整数の番号を使うことにします。
V = set( [ i for i in range(255) ] )
len(V)
-> 225 (ワクチン反対)N = set( [ i for i in range(216,226) ] )
len(N)
-> 10 (ロシアの主張を拡散)len( V – (N & V) )
-> 216 (ワクチン反対だが、ロシアの主張を拡散していない)len( N & V )
-> 9 (ワクチン反対、かつ、ロシアの主張を拡散)len( N – (N & V) )
-> 1 (ワクチンに反対していない、かつ、ロシアの主張を拡散)
それでは、それぞれの相対的な大小関係を視覚的に確認してみましょう。
それぞれの集合に含まれる要素を並べて比較します。
V – (V & N) ・・・(ワクチン反対だが、ロシアの主張を拡散していない)
-> {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 60, 61, 62, 63, 64, 65, 66, 67, 68, 69, 70, 71, 72, 73, 74, 75, 76, 77, 78, 79, 80, 81, 82, 83, 84, 85, 86, 87, 88, 89, 90, 91, 92, 93, 94, 95, 96, 97, 98, 99, 100, 101, 102, 103, 104, 105, 106, 107, 108, 109, 110, 111, 112, 113, 114, 115, 116, 117, 118, 119, 120, 121, 122, 123, 124, 125, 126, 127, 128, 129, 130, 131, 132, 133, 134, 135, 136, 137, 138, 139, 140, 141, 142, 143, 144, 145, 146, 147, 148, 149, 150, 151, 152, 153, 154, 155, 156, 157, 158, 159, 160, 161, 162, 163, 164, 165, 166, 167, 168, 169, 170, 171, 172, 173, 174, 175, 176, 177, 178, 179, 180, 181, 182, 183, 184, 185, 186, 187, 188, 189, 190, 191, 192, 193, 194, 195, 196, 197, 198, 199, 200, 201, 202, 203, 204, 205, 206, 207, 208, 209, 210, 211, 212, 213, 214, 215}V & N ・・・(ワクチン反対、かつ、ロシアの主張を拡散)
-> {224, 216, 217, 218, 219, 220, 221, 222, 223}N – (V & N) ・・・(ワクチンに反対していない、かつ、ロシアの主張を拡散)
-> {225}
はい、ワクチン反対派の多くはイデオロギーや政治的な思想などとは関係ないことが明らかですね。
算数ではVの帯グラフとNの帯グラフが重なったような図を描いて、この種の問題を解きます。
数1ではベン図を使います。
そしてPythonのプログラムでは上のようになります。
これらのどれを使って表現するにしても、必ず2つのグループの大きさ(人数)や、その重なり領域の大きさ、といった具体的な情報が必要です。
それらの1つでも分からなければ、情報を正確に網羅できないことが分かるでしょう。
このように数学やプログラミングに慣れていれば、情報の欠落に気が付きやすく、それだけダマされにくいと言えます。
補足:pythonの文法について
上のプログラムでは Python の「リスト内包表記」という文法を使って記述している部分があります。
例えば以下の行です。
V = set( [ i for i in range(255) ] )
特に、
[ i for i in range(255) ]
の部分がリスト内包表記です。
配列を表すカッコ “[ ]” の中に、繰り返し構文を1行のスタイル書いて、配列の要素を定義しています。
そして、この意味は、
「0から始まる255個の整数を並べて配列をつくりなさい」
となります。つまり1行全体としての意味は、
「0から始まる255個の整数を並べて配列をつくり、それを配列型から集合型へ変換してから、変数Vに入れなさい」
となります。
その結果として変数Vには整数0~254が並んだ集合{0,1,2,3,…253,254 }が入っていることになります。
リスト内包表記を使えば、配列の定義を簡潔に書くことができます。
ただし全てのプログラミング言語で使えるわけではありませんので、要注意です。
Python、Haskell、Scheme、Common Lisp、F#などでは使えます。
しかし古くからあるメジャーな言語、Java、JavaScript、C、C#、Objective C、BASIC、VB や、人気の Ruby や PHP などでは使えません。
論理国語の限界
今年の4月から高校も教科書改訂です。
この教科書改訂をもって10年の教育改革「高大接続教育改革」が一通り出そろうことになります。
なかでも国語は論理性が重視され、説明文や論説文の比重が非常に大きくなった一方、小説や物語文は縮小しました。一部では「文化軽視」と批判もされています。
国語の教育を通じて「論理的な思考力」を強化しようという改革の趣旨が色濃く反映されています。
一見すると正しいように思いますが、数式やプログラミング言語に比べると、やや首をかしげたくなる部分があります。
まず、実用性という意味で疑問です。
難しい文章は誰からも読まれないし、読みたくもない、というのが社会の実情です。
論理的に難解な文章を読み書きできる能力を身に着けました。
でも、その人のコミュニケーションは言葉が難しくて、誰も耳を傾けません。
それって、社会的に価値のある能力を身に着けたと言えるのでしょうか?
大いに疑問です。
次に言語の機能という意味で疑問です。
そもそも日本語のような自然言語は、正確な論理の記述には向いていません。
それを無理やり論理的にやろうとすれば、色々なローカルルールが発生し、もはや国語ではなくなるでしょう。
例えば、第1段落の主張が文章全体の結論に含まれれないような文章があったとします。
このとき、第1段落の主張を「本文に即している」と見なすのか否か、という問題があります。
この判断について世間一般では特にルールは無いでしょう。
ある人は見なさないと言うし、また別の人は見なすと言うでしょう。
ところがテストでは「即していると見なす」を正答とするものが多いです。
これは選択問題で難解な出題をしようとするあまり「消去法でしか解けない問題」を作りがちになるからです。
つまり「否定要素が無ければ正解として残す」という「解法のテクニック」が正解の理由です。
もちろん、こうした判断の基準は受験国語だけに通用するローカルルールです。
これは論理であるかのように見せかけているだけで、国語力や論理力と関係ないでしょう。
特定のゲームにだけ通用する単なるボス攻略です。
世間でこんな主張をしたら、屁理屈と言われます。
時に屁理屈は社会的な混乱を招きますので、ローカルルールはむしろ弊害とさえ言えます。
このように実際の入試問題は、世間の常識から離れたローカルルールに支えられています。
ところで、論理的な思考の記述には、日本語よりももっと適した方法があります。
数式や論理記号、プログラミング言語などです。
こうした、より形式的な言語(フォーマルメソッド)を使うべきでしょう。
私の感覚では、高校受験の問題で、すでに論理国語の難易度は上限に達しています。
それ以上に難解な論理構造を記述したいのであれば、自然言語ではなく、もっと形式的な言語を使うべきです。
論理国語のやりすぎには要注意だと思います。
論理国語で学生を消耗させている間に、また日本が衰退してしまいます。
芸術も大切です
コンピューターを使った環境として、最近はVRやメタバースが注目されています。
もちろん、マインクラフトも。
これらはみんな
「3Dのバーチャル空間で時を過ごす」
という特徴があります。
ファイナルファンタジーやフォートナイト。
こうした人気のゲームも、みんなバーチャル空間の中で遊びますよね。
これからは多くの人が3D空間で過ごすのが当たり前になります。
すると、その中で表現する絵やマークなども3Dにする必要があります。
コンピューターで絵を描くことをCGと呼びますが、これからは3DのCGを普通に描ける必要が、きっと出てくるでしょう。
それでは、コンピューターで3Dの絵を描く方法。
皆さんはご存じですか?
きっと、ほとんどの人が想像もできないと思います。
残念ながら、まだ小学校の図画工作や中学校の美術では習わないからです。
指導要領には無いため、教えられる先生が学校にはほとんどいません。
しかし時代の方が先に進みます。
自分で少しずつ調べて、簡単なものを描けるようにしておくと良いでしょう。
そして、3DのCGを描くためのフリーソフトが存在します。
Blender
おすすめは Blender というソフトです。
公式ホームページ(https://www.blender.org/)からダウンロードすることができます。
無料ですが、高機能でプロも使っています。
このソフトでアニメ映画も作られています。
WindowsでもMacでもLinuxでも動きます。
しかも、Pythonで自動化もできます。
無料で使おうと思ったら、ほぼこれ一択でしょう。
もしも新学期が始まるまで、すこし暇を持て余しているなら、挑戦してみてはいかがでしょうか。
充実した新生活を!
何はともあれ、受験お疲れさまでした。
羽を伸ばして体を休め、新学期に向けて今は十分に養生してくださいませ。
新年度はきっとステキな生活になるでしょう。
そうなるように祈っております。
そうそう、言い忘れていました。
卒業おめでとう!
いつでも教室へ遊びにおいで。
進学実績
卒塾生(進路が確定するまで在籍していた生徒)が入学した学校の一覧です。
ちなみに合格実績だけであれば更に多岐・多数にわたります。生徒が入学しなかった学校名は公開しておりません。
国公立大学
名古屋大学、千葉大学、滋賀大学、愛知県立大学、鹿児島大学
私立大学
中央大学、南山大学、名城大学、中京大学、中部大学、愛知淑徳大学、椙山女学園大学、愛知大学、愛知学院大学、愛知東邦大学、同朋大学、帝京大学、藤田保健衛生大学、日本福祉大学
公立高校
菊里高校、名東高校、昭和高校、松陰高校、天白高校、名古屋西高校、熱田高校、緑高校、日進西高校、豊明高校、東郷高校、山田高校、鳴海高校、三好高校、惟信高校、日進高校、守山高校、愛知総合工科高校、愛知商業高校、名古屋商業高校、若宮商業高校、名古屋市工芸高校、桜台高校、名南工業高校
私立高校
中京大中京高校、愛工大名電高校、星城高校、東邦高校、桜花学園高校、東海学園高校、名経高蔵高校、栄徳高校、名古屋女子高校、中部第一高校、名古屋大谷高校、至学館高校、聖カピタニオ高校、享栄高校、菊華高校、黎明高校、愛知みずほ高校、豊田大谷高校、杜若高校、大同高校、愛産大工業高校、愛知工業高校、名古屋工業高校、黎明高校、岡崎城西高校、大垣日大高校
(番外編)学年1位または成績優秀者を輩出した高校
天白高校、日進西高校、愛工大名電高校、名古屋大谷高校
※ 成績優秀者・・・成績が学年トップクラスで、なおかつ卒業生代表などに選ばれた生徒
生徒・保護者様のお友達登録はこちら
LINE登録するとプレゼントがもらえます!
【会員限定】お子様の成績と可能性を伸ばす18個のノウハウ
塾関係者様のお友達登録はこちら
LINE登録するとプレゼントがもらえます!
「zoomで簡単。オンライン授業移行の教科書」
または個別対談も可
名古屋市天白区の植田で塾を探すなら個別指導のヒーローズ!!
★ 直接のお問い合わせ ★
――――――――――――――――――――――
個別指導ヒーローズ 植田一本松校
〒468-0009
名古屋市天白区元植田1-202 金光ビル2F
TEL:052-893-9759
教室の様子(360度カメラ) http://urx.blue/HCgL