塾長です。
今回の記事は、心臓の弱い方は要注意です。
先回の記事『新教育「めんどうな事はコンピューターにやらせよう」(1)』の続編です。
先回は、
- これから世界がどうなるか
- なぜ「コンピューターの使い方」を子供たちに教えるべきか
について書きました。
今回は、コンピューターの使い方について、さらに深堀します。
- コンピューターが使えない
- コンピューターを使わせない
その恐怖を感じてもらえればと思います。
後半は、かなりショッキングなデータが登場します。
その努力はおいくら万円?
多くの場合は一生懸命努力することは良いことです。
だからと言って、常にそうとは限りません。
次の事例について、ぜひ考えてみて欲しいと思います。
同じ研修、同じ仕事
ある会社で、ある特殊機能を搭載したパソコンのマウスを新しく開発したとします。
そして、そのマウスを欲しがるターゲット層が2種類あるだろうと想定しました。
そこで同じマウスを、色合いや質感を少し変えて、2種類の商品として別々に販売することにしました。
商品名は「マウスα」と「マウスβ」に決まりました。
問題は、その値段です。
そこで係長は、社員のAさんとBさんに、それぞれの市場調査をお願いしました。
社員Aさんには「マウスα」について。似たコンセプトの商品が何種類あって、それぞれ何円で販売されているかを一覧表にまとめるように言いました。
社員Bさんには「マウスβ」について、同様の調査をお願いしました。
もちろん、パソコンの会社ですから社員にはプログラミングの研修をしてあります。
仕事の速いAさん
Aさんは、研修で習ったプログラミングを活かし、2日間で一覧表を完成させました。
1日目は、調査方法を調べました。どのホームページを見るか、どんなキーワードで探すか、などを決めました。
2日目は、調べた方法を自動化するプログラミングをしました。先輩から助言をもらったものの、半日でプログラムが完成したので、調査はあっという間に終わりました。
グラフを描くなど統計分析もしましたが、それも含めて丸2日間で終わりました。
仕事の遅いBさん
Bさんは、プログラミングを面倒に思って手作業で取り組み、5日間で一覧表を完成させました。
1日目から一覧表の作成に取り掛かったので、最初の内はAさんよりも早く仕事が進んでいると思いました。
2日目も同じ作業を続けました。色々なホームページを見て回り、似た商品を1つ見つけては、それを手作業でエクセルにコピーしていきました。
3日目も同じように続けました。たくさんあったため作業が大変でしたが、ついに一覧表を完成させました。しかし集めた情報の種類がバラバラで、間違って関係ない商品の情報をコピーしてしまったなどの作業ミスが見つかりました。
そこでチェックと修正をするために、さらに2日間かかりました。
結局、5日間かけて完成しました。
どちらの仕事の方が価値が高いか?
さて、Aさんの仕事とBさんの仕事。
最終的なアウトプットが同等であったとした場合、どちらの方が価値が高いでしょうか。
AさんとBさんは、いつもこんな感じです。
Aさんの方が、早く仕事をこなします。しかも間違えが少ないです。
Bさんは頑張ったことを主張しますが、いつもAさんよりも仕事が遅いです。
競合他社よりも早く新商品を打ち出せば、それだけ有利です。
速く仕事を終えれば、その分だけ他の仕事も進められます。
普通に考えれば、早く終えた仕事の方が、より価値が高いと思われます。
ところが現実は逆です。
コスパの悪い作業
簡単のために、AさんとBさんがの月給が、どちらも22万円だったとします。
月給ですから、どのような働き方をしても、もらえる給料は一緒です。
単純に日割り換算すれば、
2日間で完了したAさんの仕事は、2万円です。
5日間で完了したBさんの仕事は、5万円です。
おやおや。
なんと、遅かったBさんの仕事の方が、むしろAさんよりも3万円も高く評価されてしまったことになります。
それは納得のいく評価でしょうか?
Aさんは、Bさんが同じ給料であることを、どう思うでしょうか?
周りの社員は、どう思うでしょうか?
キミはAさんとBさん、どちらと一緒に仕事をしたい?
あなたはAさんとBさん、どちらの人と一緒に仕事をしたいですか?
社員の立場だったら?
お客様に接している立場だったら?
経営者の立場だったら?
そして平等を考える立場だったら?
この先もAさんとBさんが同じ評価をされてしまうのであれば、他の社員さんたちは、こうに思うでしょう。
「できるだけ、ゆっくり作業しよう」
「サボりながらやれば、効率よく給料がもらえる」
そんな会社は間もなく潰れてしまいます。
「会社が潰れる前に、転職しよう」
仕事のできる社員から逃げて行ってしまうでしょう。
努力の向きや種類が違う
Aさんは、研修で習ったプログラミングを積極的に活用しました。
「この仕事が楽になったら、他の社員や後輩たちも助かるかもしれない。」
そんなサービス精神もありました。
だから、自分の作ったプログラムを、他の社員も利用できるように公開していました。
仕事をすればするほど、コンピューターを色々な方法で使えるようになりました。
それにともなって、仕事が速く終わることが増えていきました。
Bさんは、Aさんと同じ研修を受けていました。
Aさんと動機ですが、Bさんの方が偏差値の高い大学を出ていました。
暗算や暗記が得意で、プログラミング研修の確認テストでは、むしろAさんよりも点数が高かったです。
しかし、その知識を実際の仕事には活用しませんでした。
Bさんは頭の回転が速くて、事務処理能力も高いので、手作業で競争すれば他の社員よりもテキパキとこなしました。
そのため、作業量が多くなっても、手作業のまま作業を進めてしまいがちでした。
仕事の量が増えても、仕事のやり方を改善しようとしませんでした。
同じ環境で同じ知識を与えられても、心構えが違えば結果も評価も違ってきます。
「コンピューター使おう」と思える能力
「コンピューターを使いこなす」
「プログラミング}
そんなに難しく考える必要はありません。
とりあえず次のように考えてみてください。
- 作業が多すぎ → プログラミングして楽をしよう
- 何度も何度も → プログラミングして2度目を無くそう
- 覚えきれない → コンピューターに覚えさせよう
- 調べきれない → コンピューターに調べさせよう
- 徹夜はいやだ → コンピューターにやらせて帰宅しよう
- 全員同じ作業 → だれか1人がプログラミングすればOK
- ミスできない → コンピューターにやらせよう
- 手順が難しい → コンピューターにやらせよう
- 疲れるばかり → コンピューターにやらせよう
などなど・・・
同じ作業を50回も100回も繰り返すと嫌になります。
だいたい3回目くらいで察しがつきます。
「どうしよう、このまま最後まで時間も体力も大丈夫かな。何か効率的にならないかな?」
と思い始めます。
決まった手順の作業でも、それが複雑で難しければミスが出やすいです。
だいたい最初の3回の内にミスを連発して思います。
「あとで見直しも大変になりそう。そもそもミスしない方法でできないかな?」
そういう時こそ、プログラミングを活用するチャンスです。
まだまだ日本人に欠けている発想
コンピューターを解決手段の1つとして、すぐに思い浮かべられること。
今の日本人には、この発想が学生にも社会人にも不足しています。
そもそも学習にコンピューターを活用してこなかったからです。
経験が無ければ発想ができません。
発想と言うのは、言い換えれば行動パターンです。
普段からコンピューターを活用している経験がある人ほど、発想しやすいでしょう。
調べ物をしたり、学校の宿題を提出したり、何かを発表したり、保護者のあんーとをとったり、などなど。
できるだけ多くの場面で、コンピューターを活用する経験を早くからさせておく。
それだけでも立派な教育です。
日本人は先進国の中で、コンピューターを勉強に使う時間が少ないそうです。
高性能な道具を手にしても、それをゲームにばかり使っているそうです。
この状態は早く改善する必要があります。
世界最弱レベル!? パソコンを使えない日本の生徒たち
まず、このグラフを見てください。
どう思われますか?
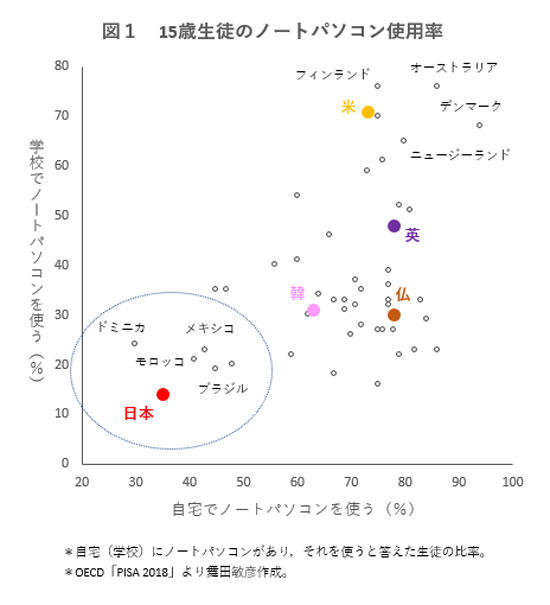
自宅や学校にノートパソコンがあり、それを使うと答えた児童の割合 ※ OECD「PISA 2018」のデータを基に教育社会学者の舞田敏彦氏が作成出典:
Newsweek 「世界で唯一、日本の子どものパソコン使用率が低下している」舞田敏彦氏(2020/1/8)
この状況は、どうやら今に始まった事ではないようです。
30年も遅れている日本
アメリカ赴任中にお子様をアメリカで育てられた方からのコメントです(原文まま)。
米国で子供を育てましたが、35年前にして、公立中学校でも、エッセイは、タイプライターかワープロで打って提出するように、手書きは、それだけで減点対象との指示。その後、大学に進学したら、当時のデスクトップPCを購入するように、それを学生寮の部屋から学内のネットに接続して履修届やリポート等を提出するようにとの指示が、30年前。
元Google日本法人社長 村上氏 談(Facebookの塾長の投稿に対するコメントより)
上のコメントについて、また別の方からもコメントをいただきました(原文まま)。
私もちょうどそのころ、米国に住んでおり、現地の中学・高校に通いましたが、まさにそうでした。当時、日本は「ワープロは手書き文化を損なうので禁止すべきだ」ということが真面目に議論されていて、子ども心に日本の衰退が予測できて悲しかったですね。
STUDY PLACE 翔智塾 代表 中村先生 談(Facebookの塾長の投稿に対するコメントより)
また少し違った角度から、紙で提出してはいけない理由を解説していただきました(原文まま)。
Double spaced on one side of the page ですね.これは大事な点で,提出物は「コメントをしてもらえるように」というのが鉄則で,間違えてsingle spaced で提出すると傲慢ととられます.数学は例外で手書きもたいていO.K.とおもいます.
日本の英文学会は長いことsubmitした原稿は「決定稿」でレフェリーコメントによって改善する,というシステムはありませんでした.アメリカの文学会はsubmitした原稿を採択する場合にはレフェリーの意見により,書き直しをお願いすることもあります.これはよりよい論文を本誌に掲載したいと思っているからです.というのがはっきり書いてあります.
そして「必ず」推敲が必要,自分がいいたいことは自分が一番わかっていない,という認識でしょうか?そのため,消しゴムを使うのは最悪で,editの後がわかるように証拠を残す,editがあるのが大前提でinvitation for commentsという形で余白をつくる.名古屋大学 宇澤教授(Facebookの塾長の投稿に対するコメントより)
あぁ、なんということでしょう。
日本は30年も遅れている!
いや、最悪35年も・・・
教育現場においてITSの活用で遅れている?
単にそれだけではありません。
「自分が言いたいことは自分が一番わかっていない」
「エビデンスを残す」
このような科学的な思考の育成が、そもそも一歩も二歩も遅れています。
そして、エビデンスを持つということは、30年前からその手のビッグデータが蓄積されているということです。
そのデータ自体が、また次の研究や開発の対象として価値を生みます。
ソフトや教育の資産価値を高めていく土壌がアメリカにはあるのです。
日本には、その土壌がまだありません。
ITSが遅れるということは、このように2重にも3重にも色々なことが遅ることになります。
反省すべき過去30年
その結果、次のような差が生まれてしまうのです。
平成元年と平成30年の「世界時価総額ランキング」を比較すると、バブル期の日本が相当ヤバかったし世界の変動も見て取れる
この状況について、もちろん政府は問題視してます。
政府どころか、東京都でもこんな資料を作っているくらいです。
そしてこんな記事まで。
「これが長期停滞の元凶…コロナ禍が暴いた日本IT化「絶望的な遅れ」」現代ビジネス 2020/8/23 野口 悠紀雄氏の記事より
挙げればきりがありません・・・
この状況はどうしたら改善できるでしょうか?
まず、この状況は子供たちではなく、大人たちの責任です。
私たちが子供に何をしてあげられるか?
子供たちにかける言葉を間違わないことです。
そこから考えなくてはいけません。
たとえば、読書感想文を
「原稿用紙に書いて提出しなさい」
というのを
「メールで送りなさい」
としたり、あるいは少なくとも
「パソコンで打って印刷したものを提出しなさい」
などとしなければ変わりません。
大人が
「紙に書け」
と言えば、子供はコンピューターではなく紙に書きます。
そのような、何気ない私たちの慣れ切った言動のパターンが、子供たちの将来性を奪ってきたのだとしたら・・・
そう考えると、子供たちに申し訳なく思います。
日本の私たちは、自身の「当たり前」が世界の非常識になっている自覚を持たざるを得ない。
そういうところまで来ています。
大人の好き嫌いが子供たちの将来性を奪っていないか?
もうすでに身の回りはコンピューターだらけです。
これからはコンピューターが使えて当たり前になります。
大人の皆さんは、まだコンピューターが良く分からなかったり、あるいは苦手だったりするかもしれません。
- プログラミング? ただの流行りでしょ。
- プログラミング? 本物の教育とは言えないね。
そんな評価や食わず嫌いを言う人もあるでしょう。
大人は自分の生活を自分の責任で生きています。
ですから、こんな好き勝手を言ってもOKです。
しかし、自身の主義主張や苦手意識を理由に、子供たちからコンピューターを利用するチャンスを奪ってはいけません。
大人たちの今がどうだろうと、子供たちの将来は、
コンピューターが使えて当たり前!
になるなのです。
もっと辛いことを言えば、海外では30年前から、すでに当たり前になっています。
後で書きますが、知らないのは日本の大人たちだけです。
大人の皆さん、子供たちの将来を奪っていませんか?
子供たちの将来は、今の大人たちの好き嫌いとは関係ないはずです。
笑えるようで笑ってられない。こんなことまで手作業!?
日本をむしばむ悪しき習慣を列挙してみましょう。
- 1つの漢字を「20回ずつ書いてこい」などという類の宿題
- 重箱の隅をつつくような問題に対応するためのテスト対策
- 感想文や小論文の原稿を何度も手書きで提出させる
- 自由研究の提出物がいまだに紙や原稿用紙
- 提出書類のフォーマットが厳格で、少しでも間違えると無効
- 先生が講義ノートを見ながら板書し、それを生徒たち全員がノートに写す
- ハサミとノリでプリントの原稿を作る
- 印刷物のフォーマットをエクセルで作る
- わざわざ議事録を作る
- インターネットエクスプローラ(IE)でなければ動かない
- コロナ禍でもハンコを押すために出社
- 取引書類を紙で取っておかなければならない
- 決裁権のない人が会議に参加して「持ち帰って検討します」と言う
- 1人が作って配ればよいのに、毎回みんなで作っている
- お役所Aがお役所Bの書類を持って来いと言う
- データがCDやFAXで送られて来る
みなさん、他にどんなものを思いつきますか?
誰にでも手にしている技術を使わないということは、次の世代に不当な苦労を強いることになります。
自分の行動が老害になっていないか?
常にチェックする必要があります。
少なくとも、子供たち、学生のみなさんは、上のような行動を参考にしてはいけません。
反面教師にしてください。
若い人がコンピューターやアプリを使って何気ない改善提案をしてきたとき、それを目上の人がつぶさないことです。
ちゃんと1度受け止めて、真剣に対応しましょう。
3万円でできるコンピューター環境
以前にこんな記事を書きました。ご参考になれば。
予算3万円!子供のために立派なパソコンとソフトウェアを揃える方法
生徒・保護者様のお友達登録はこちら
LINE登録するとプレゼントがもらえます!
【会員限定】お子様の成績と可能性を伸ばす18個のノウハウ
塾関係者様のお友達登録はこちら
LINE登録するとプレゼントがもらえます!
「zoomで簡単。オンライン授業移行の教科書」
または個別対談も可
名古屋市天白区の植田で塾を探すなら個別指導のヒーローズ!!
★ 直接のお問い合わせ ★
――――――――――――――――――――――
個別指導ヒーローズ 植田一本松校
〒468-0009
名古屋市天白区元植田1-202 金光ビル2F
TEL:052-893-9759
教室の様子(360度カメラ) http://urx.blue/HCgL